Estimation in Poisson Noise
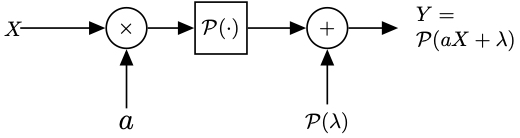 |
The Poisson noise channel with the input random variable \(X\), the scaling factor \(a\), the dark current parameter \(\lambda\), and the ouput random variable \(Y\). |
Brief Overview
Poisson noise models are an important set of models with a wide range of applications. Concretely, for an input random variable \(X \ge 0 \) the Poisson noise channel is dictated by the following conditional probability mass function (pmf) of the output random variable \(Y\):
\[ P_{Y|X}(y|x) = \frac{1}{y!} (ax+\lambda)^y e^{- (ax+\lambda)}, x\ge 0, \, y=0,1, \ldots \quad (*) \]
where \(a>0\) is a scaling factor and \(\lambda \ge 0\) is a non-negative constant called the dark current parameter. In words, conditioned on a non-negative input \(X=x\), the output of the Poisson channel is a non-negative integer-valued random variable \(Y\) that is distributed according to \((*)\). In \((*)\) we use the convention that \(0^0=1\).
The random transformation of the input random variable \(X\) to an output random variable \(Y\) by the channel in \((*)\) will be denoted by
\[ Y= \mathcal{P}(aX+\lambda). \quad (**) \]
The transformation in \((**)\) is depicted on top of this page. It is important to note that the operator \(\mathcal{P}(\cdot)\) is not linear, and it is not true that \( \mathcal{P}(aX+\lambda)= a\mathcal{P}(X)+\lambda\). Using the language of laser communications, the \(aX\) represents the intensity of a laser beam at the transmitter and \(Y\) represents the number of photons that arrive at the receiver equipped with a particle counter (i.e., a photodetector). The dark current parameter \(\lambda\) represents the intensity of an additional source of noise or interference, which produces an extra \(\mathcal{P}(\lambda)\) photons at a particle counter.
Journal Papers
A. Dytso, M. Fauß, H. V. Poor, “The Vector Poisson Channel: On the Linearity of the Conditional Mean Estimator,” arXiv:2003.08967.
A. Dytso, H. V. Poor, ‘‘Estimation in Poisson Noise: Properties of the Conditional Mean Estimator," IEEE Transactions on Information Theory, Vol. 66, No. 7, July 2020.
Conference Papers
A. Dytso and H. V. Poor, “Properties of The Conditional Mean Estimator in Poisson Noise,” in Proc. IEEE Inf. Theory Workshop, Visby, Sweden, August 2019.
A. Dytso and H. V. Poor, “On Stability of Linear Estimators in Poisson Noise,” Asilomar Conference on Signal, Systems, and Control, Pacific Grove, CA, USA, October 2019