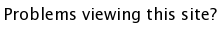back to structure index

Perovskite Structure and Derivatives

SrTiO3 - Cubic Perovskites

The general formula for a perovskite is ABO3 where A and B are cations. The easiest way to visualize the structure is in terms of the BO6 octahedra which share corners infinitely in all 3 dimensions, making for a very nice and symmetric structure. The A cations occupy every hole which is created by 8 BO6 octahedra, giving the A cation a 12-fold oxygen coordination, and the B-cation a 6-fold oxygen coordination. In the example shown below, (SrTiO3, download cif) the Sr atoms sit in the 12 coordinate A site, while the Ti atoms occupy the 6 coordinate B site. There are many ABO3 compounds for which the ideal cubic structure is distorted to a lower symmetry (e.g. tetragonal, orthorhombic, etc.)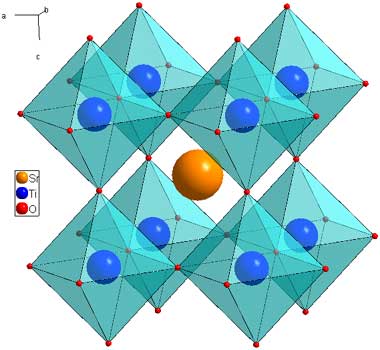

Sr₂FeMoO₆ - Double Perovskites

The double perovskite structure is so named because the unit cell of is twice that of perovskite. It has the same architeture of 12 coordinate A sites and 6 coordinate B sites, but two cations are ordered on the B site. The example shown here is Sr₂FeMoO₆ (download cif). The Fe and Mo atoms have ordered in a 3D chessboard type fashion.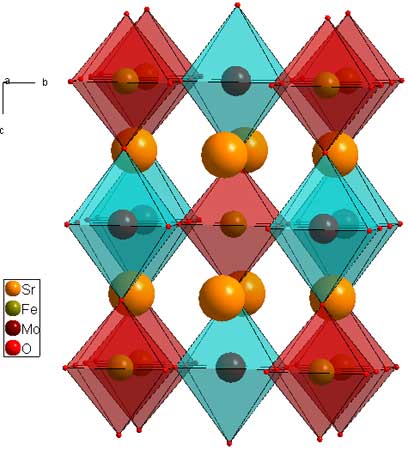

Layered Perovskties: Ruddleson-Popper, Aurivillius and Dion-Jacobson phases

Layered perovskites consist of infinite 2D slabs of the ABO3 type structure which are separated by some motif. The general formula for the layers is: A_(n-1)B_(n)O_(3n+1). The differentiating characteristics for the layered perovsktes are 1) the motif which separates the layers, and 2) the offsetting of the layers from eachother.
In this formula, "n" indicates the size of the 2D slabs. n=1 means the slab is one BO6 octahedron thick. n=2 means two BO6 octahedra thick, etc. The clearest examples of this are the n=1 and n=2 Ruddleson-Popper phases Sr₂RuO₄ (download cif), and Sr₃Ru₂O₇ (download cif). For these phases, Sr is the A cation, and Ru is the B cation. The separating motif is a layer of Sr2, and the perovskite slabs are offset by a (1/2,1/2) translation. It is possible, and perhaps appropriate to think of Ruddleson Popper phases as the general formula as (A_(n+1)B_nO_(3n+1), indicating that the outer A atoms are part of the 2D perovskite slabs, but I think of them as {A₂}-{A_(n-1)B_nO_(3n+1)} because that relates them more consitently to the other layered perovsktes.


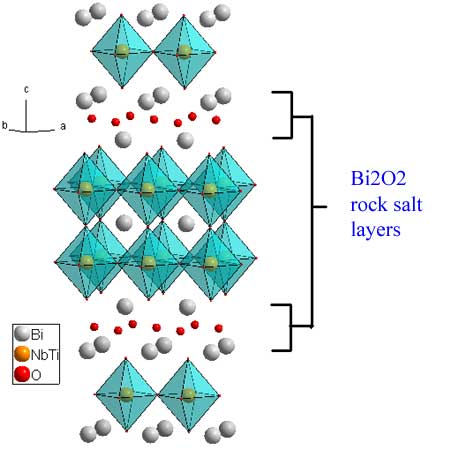
The n=2 phase Bi₃TiNbO₉ (download cif) is representative of the Aurivillius phases, for which the general formula is {Bi₂O₂}-{A_(n-1)B₂O₇}. For this phase, Ti and Nb are statistically dispersed on the B site. The formula can be re-written as: {Bi₂O₂}-Bi(Ti,Nb)₂O₇. The separating motif for ALL Aurivillius phases is a rock-salt Bi₂O₂ layer. For this example, Bi is also the A cation, but that needn't be the case. Again the displacement of the perovskite slabs is a (1/2,1/2) translation.


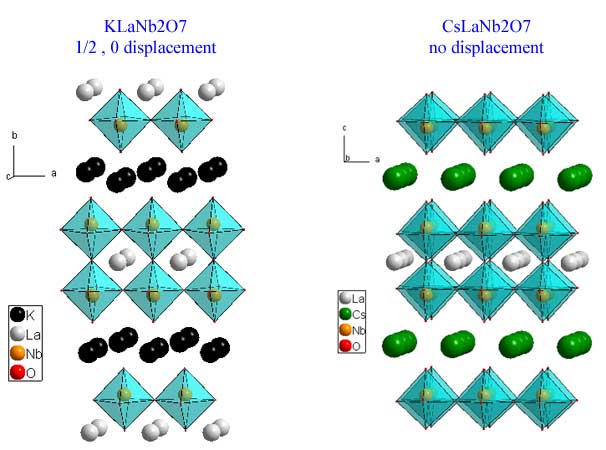
The Dion-Jacobson phases have the general formula M⁺¹A_(n-1)B_nO_(3n+1). They differ from the other layered phases by having a layer of alkali metal as the separating motif. Below is a picture of KLaNb2O7 (download cif) and and CsLaNb2O7 (download cif). The displacement of the perovskite slabs is either (1/2,0) or nothing at all depending upon which alkali metal is used as the separating motif.


back to structure index