9.2 Continuum Elements
9.2.0 Analysis Options
In one dimension the element is
defined by 2 nodes. If the number of
spatial dimension NSD = 1 (defined in Section 2.1), usual rod theory is used,
and the element is assumed to have axial kinematics only. Otherwise, i.e. if NSD > 1, the element is
assumed to be aligned with the 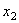 -axis in the global reference frame (
-axis in the global reference frame (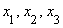 ), and NSD kinematics in directions
), and NSD kinematics in directions 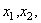 etc., are assigned to each node.
etc., are assigned to each node.
In two dimensions the element may be
used in triangular (3 node or 6 node) or quadrilateral (4 node, 8 node or 9
node) form for plane and axisymmetric analysis.
The nodes of the element must be input in counterclockwise order in the
order shown in Figure 9.2.0.1. The plane
of analysis is assumed to be the 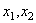 plane, and the element
is assumed to have unit thickness in the plane option. In axisymmetric analysis the radial direction
is specified as the
plane, and the element
is assumed to have unit thickness in the plane option. In axisymmetric analysis the radial direction
is specified as the 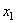 -axis. Reduced / selective numerical integration and the mean
dilatational formulation may be employed to improve element behavior in various
situations. These options should be activated only by users fully knowledgeable in
their use.
-axis. Reduced / selective numerical integration and the mean
dilatational formulation may be employed to improve element behavior in various
situations. These options should be activated only by users fully knowledgeable in
their use.
In three dimensions the element may
be used in tetrahedral (10 or 4 node), wedge (6 node or 15 node) or brick (8
node or 20 node) form. The nodes of the
element must be input in the order shown in Figure 9.2.0.1. Reduced/selective numerical integration and
the mean dilatational formulation may be employed to improve element behavior
in various situations. These options should be activated only by
users fully knowledgeable in their use.
Stresses/strains in the global coordinate
system, principal stresses/strains, maximum shear stress/strain and angle of
inclination, in degrees, of principal states are output at the element
centroid, which is generally the point of optimal accuracy. All shear strains are reported according to
the "engineering" convention (i.e. twice the value of the tensor
components).
In the following, NSD = number of
spatial dimension; NDOF = total number of degrees of freedom; and NED = element
nodal local degrees of freedom.
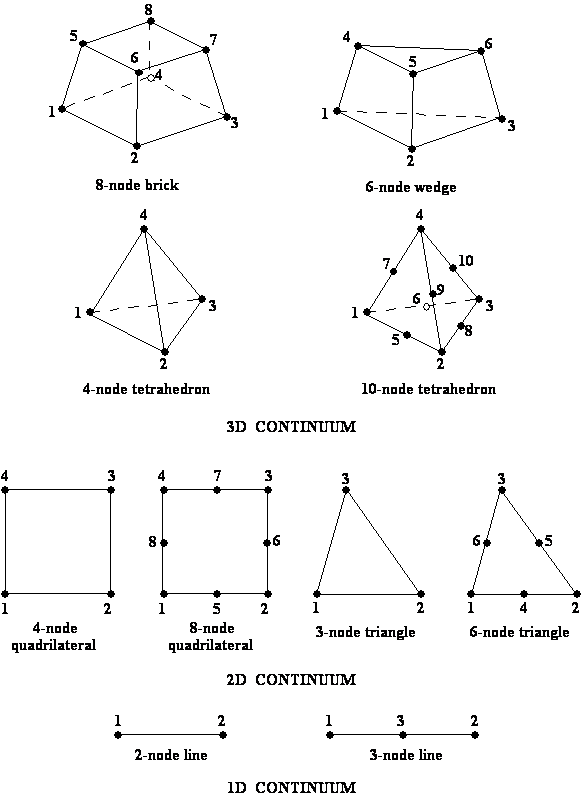
Figure
9.2.0.1 Continuum Elements
9.2.0.1 Solid
Equation
QDC_SOLID
Element_name = QDC_Solid, etc…
< stress material data >
< body force data >
< connectivity data >
< field output data >
The element is used for solution of
the following equations:
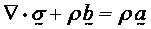
where
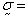 solid stress,
solid stress, 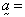 solid acceleration,
solid acceleration, 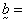 body force (per
unit mass) and
body force (per
unit mass) and 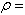 mass density. NSD solid kinematic degrees of freedom are
assigned to each node, in the
mass density. NSD solid kinematic degrees of freedom are
assigned to each node, in the 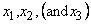 directions,
respectively.
directions,
respectively.
·
For saturated porous media applications
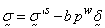
where 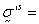 solid effective
stress,
solid effective
stress, 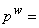 pore fluid pressure;
pore fluid pressure; 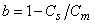 ; Cs = solid grains compressibility; Cm
= solid matrix compressibility;
; Cs = solid grains compressibility; Cm
= solid matrix compressibility; 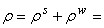 total mass density,
total mass density, 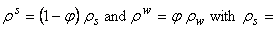 solid mass density,
solid mass density,
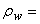 fluid mass density and
fluid mass density and
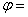 porosity. For fully undrained (viz., no diffusion)
cases, the pore fluid pressure is determined from the computed solid velocities
through the following equation:
porosity. For fully undrained (viz., no diffusion)
cases, the pore fluid pressure is determined from the computed solid velocities
through the following equation:
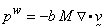
where 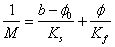 ;
; 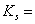 solid grains modulus,
solid grains modulus, 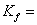 fluid bulk modulus
fluid bulk modulus
·
For multi-phase fluid flow applications:
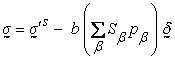
where 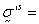 solid effective
stress;
solid effective
stress; 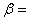 fluid phase number (
fluid phase number (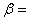 1, number_of_phases);
1, number_of_phases); 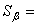 degree of saturation;
degree of saturation; 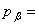 fluid pressure;
fluid pressure;
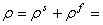 total mass density;
total mass density; 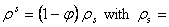 solid mass density and
solid mass density and
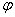 = porosity;
= porosity; 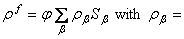 fluid phase mass
density.
fluid phase mass
density.
·
For thermo solids:
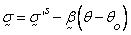
where 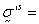 solid effective
stress,
solid effective
stress, 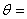 temperature and
temperature and 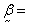 thermal moduli
(second-order tensor).
thermal moduli
(second-order tensor).
·
For piezoelectric solids:
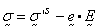
where 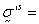 solid effective
stress,
solid effective
stress, 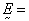 electric field (viz.,
electric field (viz., 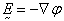 where
where 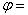 electric potential),
and
electric potential),
and 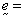 piezoelectric
constants (third-order tensor, viz.,
piezoelectric
constants (third-order tensor, viz., 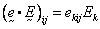 ).
).
Implementation
Issues
For coupled problems, in the
implementation we adopted, the dependent variables are the velocity and the
pressure and/or temperature, and a Petrov-Galerkin formulation is used to
circumvent restrictions of the Babuska-Brezzi condition. In particular, equal-order interpolations are
used for both the velocity and the pressure.
References / Bibliography
1. Babuska, I.,
"Error Bounds for Finite Element Method," Numer. Math, 16 (1971), 322-333.
2. Brezzi, F..,"On the Existence, Uniqueness
and Approximation of Saddle-Point Problems Arising from Lagrange
Multipliers," Rev. Francaise
d'Automatique Inform. Rech. Oper., Ser.
Rouge Anal. Numer. 8, R-2 (1974) 129-151.
3. Hughes, T.J.R, Franca, L.P. and Balestra, M., "A New
Finite Element Formulation for Computational Fluid Dynamics: V. Circumventing
the Babuska-Brezzi Condition: A Stable Petrov-Galerkin Formulation of the
Stokes Problem Accommodating Equal-Order Interpolations," Comp. Meth. Appl. Mech. Eng., Vol. 59
(1986) 85-99.
9.2.0.2 Fluid Equation
QDC_FLUID
Element_name = QDC_Fluid , etc…
< stress material data >
< body force data >
< connectivity data >
< field output data >
The element is used for solution of
the following equations:
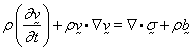
where
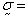 stress,
stress, 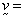 velocity,
velocity, 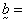 body force (per unit
mass),
body force (per unit
mass), 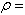 mass density. The fluid stress is given by the following
equation:
mass density. The fluid stress is given by the following
equation:
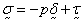
where
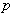 is the pressure, and
is the pressure, and 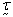 the viscous stress
tensor. For isotropic fluids the
following viscous relation is used:
the viscous stress
tensor. For isotropic fluids the
following viscous relation is used:
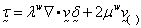
where
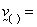 symmetric part of the velocity gradient, i.e., in components
form:
symmetric part of the velocity gradient, i.e., in components
form:
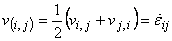
and
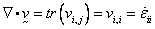
In
the above equation 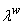 and
and 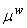 are the viscosity
coefficients (also referred to as the Lamé coefficients). For incompressible flows,
are the viscosity
coefficients (also referred to as the Lamé coefficients). For incompressible flows, 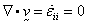 . In our
implementation, isothermal incompressible and "slightly compressible"
flows are considered.
. In our
implementation, isothermal incompressible and "slightly compressible"
flows are considered.
For incompressible flows, the pressure is determined from the computed
velocities through the following equation:
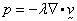
where
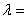 a penalty
parameter. Clearly,
a penalty
parameter. Clearly, 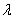 must be large enough
so that the compressibility and pressure errors are negligible, yet not so
large that numerical ill-conditioning ensues.
The criterion used is (see [1]):
must be large enough
so that the compressibility and pressure errors are negligible, yet not so
large that numerical ill-conditioning ensues.
The criterion used is (see [1]):
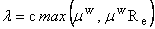
where
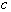 is a constant which
depends only on the computer word length (it is independent of the mesh
parameter
is a constant which
depends only on the computer word length (it is independent of the mesh
parameter 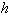 ) and
) and 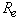 is the Reynolds
number. Numerical studies reveal that
for floating-point word lengths of 60 to 64 bits,
is the Reynolds
number. Numerical studies reveal that
for floating-point word lengths of 60 to 64 bits, 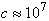 . The Reynolds number is computed as
. The Reynolds number is computed as
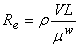
where
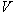 and
and 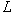 are
"characteristic" velocity and length, respectively. The characteristic velocity
are
"characteristic" velocity and length, respectively. The characteristic velocity 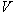 is usually taken to be
the maximum expected velocity in the flow, and
is usually taken to be
the maximum expected velocity in the flow, and 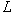 is taken as a major
dimension of the problem (e.g., the diameter).
is taken as a major
dimension of the problem (e.g., the diameter).
For "slightly compressible" flows, the pressure is determined
through the following equation:
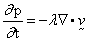
where
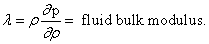
Implementation
Issues
In the implementation we adopted,
the convective force is treated explicitly (to avoid non-symmetric
matrices). This engenders some stability
restrictions. Stability analyses
indicate that if no iterations are performed, the upwind scheme used (see
Section 9.2.1) for the convection are stable if 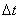 satisfies a Courant
condition [1], viz.,
satisfies a Courant
condition [1], viz.,
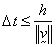
where
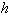 = mesh size parameter,
and
= mesh size parameter,
and 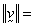 velocity magnitude for
the element. The above inequality must
be satisfied for each finite element in the mesh. (Note it is solely a convection condition and
in particular is independent of the Reynolds number.)
velocity magnitude for
the element. The above inequality must
be satisfied for each finite element in the mesh. (Note it is solely a convection condition and
in particular is independent of the Reynolds number.)
For fluid applications, NSD fluid
kinematic degrees of freedom are assigned to each node, in the 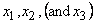 directions,
respectively. The time integration must
be performed with a hyperbolic time integrator (see Section 12.2) as the
resulting initial boundary value problem is treated as parabolic-hyperbolic.
directions,
respectively. The time integration must
be performed with a hyperbolic time integrator (see Section 12.2) as the
resulting initial boundary value problem is treated as parabolic-hyperbolic.
Remark: For isothermal incompressible flows, there is
no energy balance or temperature equation.
Thus the pressure variable enters the system of equations only through
its derivative and therefore 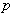 can be determined only
up to an arbitrary constant. This means that the pressure must be specified
externally somewhere in the flow field.
can be determined only
up to an arbitrary constant. This means that the pressure must be specified
externally somewhere in the flow field.
References / Bibliography
1. Hughes et al., "Review of Finite Element
Analysis of Incompressible Viscous Flows by the Penalty Function
Formulation," J. Comp. Phys., 30, No. 1, (1979), 1-60.
2. Hughes, T.J.R., et
al.,"Lagrangian-Eulerian Finite Element Formulation for Incompressible
Flows," Comp. Meth. Appl. Mech. Eng.,
Vol. 29, (1981), 329-349.
3. Prevost, J.H., and Hughes,
T.J.R.,"Dynamic Fluid-Structure-Soil Interaction," ASCE Publication on Geotechnical Practice in
Offshore Engineering, (1983),
133-143.
9.2.0.3 Stokes Flow Equation
QDC_STOKES
Element_name = QDC_Stokes , etc…
< stress material data >
< body force data >
< connectivity data >
< field output data >
The element is used for solution of
the following equations:
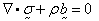 (momentum
balance)
(momentum
balance)
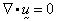 (incompressibility
condition)
(incompressibility
condition)
where
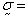 Cauchy stress,
Cauchy stress, 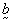 = body force
(per unit mass),
= body force
(per unit mass), 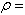 mass density. The fluid stress is given by the following
equation:
mass density. The fluid stress is given by the following
equation:
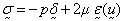
where
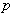 is the pressure, and
is the pressure, and 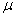 is the dynamic
viscosity;
is the dynamic
viscosity; 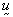 is the velocity vector, and
is the velocity vector, and 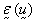 is the symmetrical
part of the velocity gradient.
is the symmetrical
part of the velocity gradient.
Implementation
Issues
In the implementation we adopted,
the dependent variables are the velocity and the pressure, and a
Petrov-Galerkin formulation is used to circumvent restrictions of the
Babuska-Brezzi condition. In particular,
equal-order interpolations are used for both the velocity and the pressure.
References / Bibliography
1. Babuska, I.,
"Error Bounds for Finite Element Method," Numer. Math, 16 (1971), 322-333.
2. Brezzi, F..,"On the Existence,
Uniqueness and Approximation of Saddle-Point Problems Arising from Lagrange
Multipliers," Rev. Francaise
d'Automatique Inform. Rech. Oper., Ser.
Rouge Anal. Numer. 8, R-2 (1974) 129-151.
3. Hughes, T.J.R, Franca, L.P. and Balestra, M., "A New
Finite Element Formulation for Computational Fluid Dynamics: V. Circumventing
the Babuska-Brezzi Condition: A Stable Petrov-Galerkin Formulation of the
Stokes Problem Accommodating Equal-Order Interpolations," Comp. Meth. Appl. Mech. Eng., Vol. 59
(1986) 85-99.
9.2.0.4 Scalar Convection-Diffusion Equation
QDC_TRANSPORT
Element_name = QDC_Transport , etc…
< scalar diffusion material data >
< body force data>
< connectivity data >
The element is used for solution of
the following scalar convection-diffusion equation:
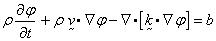
where
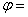 concentration,
concentration, 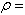 mass density,
mass density, 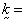 diffusivity =
diffusion/dispersion coefficient matrix,
diffusivity =
diffusion/dispersion coefficient matrix, 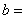 body force, and
body force, and 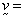 given flow
velocity. The Peclet number is defined as follows:
given flow
velocity. The Peclet number is defined as follows:
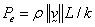
where
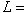 characteristic length.
For
characteristic length.
For 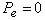 a purely diffusive
solution is obtained, whereas for
a purely diffusive
solution is obtained, whereas for 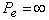 solution to the
first-order wave equation is obtained. For convection-diffusion (parabolic
mode) and advection-diffusion (elliptic mode) one degree of freedom is assigned
to each node for the concentration
solution to the
first-order wave equation is obtained. For convection-diffusion (parabolic
mode) and advection-diffusion (elliptic mode) one degree of freedom is assigned
to each node for the concentration 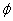 . In the
implementation we adopted, the connective force is treated implicitly and a non-symmetric
linear-solver must therefore be used (see Section 12.4). A stabilized SUPG formulation is used.
. In the
implementation we adopted, the connective force is treated implicitly and a non-symmetric
linear-solver must therefore be used (see Section 12.4). A stabilized SUPG formulation is used.
References / Bibliography
1. Brooks,
A.N. and Hughes, T.J.R., “Streamline Upwind/Petrov-Galerkin Formulations for
Convection Dominated Flows with Particular Emphasis on the Incompressible
Navier-Stokes Equations,” Computer
Methods in Applied Mechanics and Engineering, Vol. 32, (1982), pp. 199-259.
9.2.0.5 Helmoltz/Laplace Equation
QDC_HELMOLTZ
Element_name = QDC_Helmoltz , etc…
< material data >
< connectivity data >
The element is used for solution of
the following scalar equation:
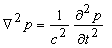
where
p = pressure and c = wave speed 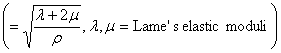 .
.
One
degree of freedom is assigned to each node for the pressure. The element may be used to solve the Laplace equation (elliptic mode) and the Helmoltz
equation (hyperbolic mode).
9.2.0.6 Mesh Motion Equation
QDC_ALE
Element_name = QDC_ale , etc…
< connectivity data >
The element is used to compute the
mesh displacement field in arbitrary Lagrangian-Eulerian (ALE) models (see
Section 5.4), by solving the following vector Laplace
equation:
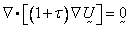
subject
to appropriate prescribed displacement boundary conditions at the moving
boundary. The moving boundary is
composed of the moving fluid-solid interfaces as well as the oscillating free
surfaces. The parameter 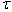 is a bounded,
nondimensional function designed to prevent the inversion of small elements
(see e.g. [1]) as follows. For each
element
is a bounded,
nondimensional function designed to prevent the inversion of small elements
(see e.g. [1]) as follows. For each
element 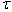 is defined as:
is defined as:
 (1)
(1)
where
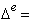 area (or volume in 3D)
of the current element,
area (or volume in 3D)
of the current element,
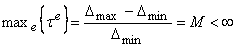 (2)
(2)
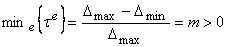 (3)
(3)
Remarks:
For the degenerate case of a uniform mesh, 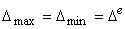 and the Laplace equation works well without the additional
constraint equation over the element, and
and the Laplace equation works well without the additional
constraint equation over the element, and 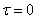 .
.
References / Bibliography
1.
Masud, A. and T.J.R. Hughes, "A Space-time Finite
Element Method for Fluid-structure Interaction," SUDAM Report No. 93-3, Stanford
University, Stanford, CA,
(1993).
![]() -axis in the global reference frame (
-axis in the global reference frame (![]() ), and NSD kinematics in directions
), and NSD kinematics in directions ![]() etc., are assigned to each node.
etc., are assigned to each node.![]() plane, and the element
is assumed to have unit thickness in the plane option. In axisymmetric analysis the radial direction
is specified as the
plane, and the element
is assumed to have unit thickness in the plane option. In axisymmetric analysis the radial direction
is specified as the ![]() -axis. Reduced / selective numerical integration and the mean
dilatational formulation may be employed to improve element behavior in various
situations. These options should be activated only by users fully knowledgeable in
their use.
-axis. Reduced / selective numerical integration and the mean
dilatational formulation may be employed to improve element behavior in various
situations. These options should be activated only by users fully knowledgeable in
their use. 
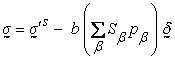
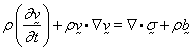
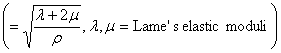 .
.