Transformation Data Records

  A Transformation Data Set is denoted by a `KEY' of 50 in the data set header record. The ASSEMBLE command, described in the User Manaual, enables the creation of assemblies from a number of models. It may be necessary to transform some of the models to achieve the correct spatial relationship between them in the assembly. The transformation data set is used to define these transformations via a transformation matrix. More than one transformation matrix may be associated with a single model, each matrix being defined as follows:

IKEY,NUMB

Where:

IKEY = -1 for transformation data

= -3 for data set delimiter

NUMB = the transformation identification number

To be written in the format:

FORMAT(1X, I2, I5)

or: FORMAT (1X, I2, I10) for 10 digit transformation number format

Followed by four lines:

IKEY, TRANS1, TRANS2, TRANS3, TRANS4
IKEY, TRANS5, TRANS6, TRANS7, TRANS8
IKEY, TRANS9, TRANS10, TRANS11, TRANS12
IKEY, TRANS13,TRANS14, TRANS15, TRANS16

In the format:

FORMAT(1X,I2,4E12.5)

Where:

IKEY = -2
TRANS1 to TRANS16 define the transformation matrix

Notes:

1.

The matrix is stored such that terms 1,2,3,5,6,7,9,10, and 11 are rotation terms, term 13 is shift in x , term 14 is shift in y , term 15 is shift in z , and term 16 is the scale term. Terms 4,8, and 12 are X ,Y , and Z perspective terms, and are generally not used. Terms 1 to 16 refer to the following positions in the transformation matrix: $$\left[ XT,YT,ZT,1 \right] = \left[ T \right] \left[ A \right]$$

$$\left[ XT,YT,ZT,1 \right] = \left[ \begin{array} {cccc} 1& ... ...t] \left[ \begin{array} {c} X\\ Y\\ Z\\ 1 \end{array} \right]$$

The matrices for some basic transformations are defined below:

A Translation (X,Y,Z ) :

$$T = \left( \begin{array} {cccc} 1& 0& 0& X \\ 0& 1& 0& Y\\ 0& 0& 1& Z\\ 0& 0& 0& 1 \end{array} \right)$$

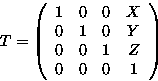
A Rotation about the X axis through angle $\alpha$:

$$T = \left( \begin{array} {cccc} 1& 0& 0& 0 \\ 0& \cos\alph... ... \sin\alpha & \cos\alpha & 0\\ 0& 0& 0& 1 \end{array} \right)$$

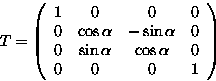
A Rotation about the Y axis through angle $\beta$:

$$T = \left( \begin{array} {cccc} \cos\beta & 0& \sin\beta & ... ...in\beta & 0 & \cos\beta & 0\\ 0 & 0& 0& 1 \end{array} \right)$$

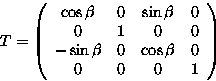
A Rotation about the Z axis through angle $\gamma$:

$$T = \left( \begin{array} {cccc} \cos\gamma & -\sin\gamma & ... ...ma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0& 0& 1 \end{array} \right)$$

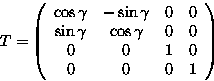
Scale Factor S , centre at origin:

$$T = \left( \begin{array} {cccc} 1& 0& 0& 0 \\ 0& 1& 0& 0 \\ 0& 0& 1& 0 \\ 0& 0& 0& 1/S \end{array} \right)$$

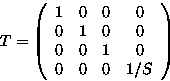
It may be necessary to rotate, translate and scale a model to include it in an assembly. If this is the case, a compound transformation matrix will be needed. The compound matrix may be determined by expressing the compound transformation as a combination of the five simple transformations given above. These matrices must then be multiplied together in the correct order to give the compound transformation matrix.

For example, it is desired to rotate a model about some point in space (m_x,m_y,m_z ), scale it by a factor S about this point, and translate the model so that the centre of rotation is moved to a point (t_x,t_y,t_z ). The compound transformation matrix would be determined in the following way:

$$\begin{eqnarray*} \left[ T \right] & = & {\left[ \begin{array} {cccc} 1 & 0 & 0 ... ...-m_{y}\\ 0 & 0 & 1 & -m_{z}\\ 0 & 0 & 0 & 1 \end{array} \right]} \end{eqnarray*}$$

Once the components of the compound matrix have been found they may then be related to the correct term number (1 to 16) and entered in the format specified above.

2.

A maximum of 100 transformations are allowed for a particular model.