



 Spherically
Symmetric Theory
Spherically
Symmetric TheorySince the early 1950's, it has been recognized that the symmetrical burning of an isolated droplet represents an ideal situation in which to study the complex coupling of chemical reactions and two-phase flow with phase change. Prior to computers, the simplified geometry of the combustion environment, along with certain simplifying assumptions concerning physical and chemical processes, permitted mathematical simplifications of the problem, and led to simple descriptions of the combustion process. Initially, these studies provided a fundamental foundation upon which to develop more applied, empirical descriptions of spray combustion. The combustion of a single, isolated liquid droplet in an infinite oxidizing medium is shown schematically in Figure 1.
In this geometrical configuration, fuel vaporizes at the droplet surface and diffuses outward while oxidizer diffuses inward from the ambient environment. The fuel and oxidizer react stoichiometrically, resulting in a zone of intense reaction (i.e. a non-premixed flame). Heat is transported via conduction and radiation outward from the flame to infinity and inward back to the droplet surface. The heat deposited at the droplet surface is balanced by the evaporation process at the vapor/liquid interface.
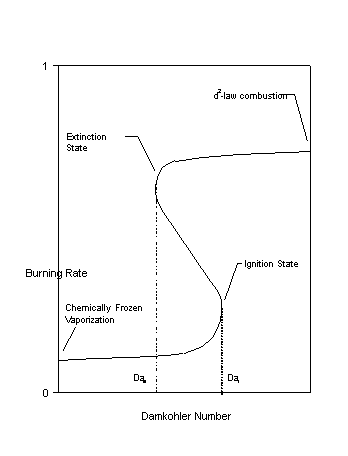
The "classical" d2-law for droplet combustion was first formulated in the 1950s by assuming that gas-phase chemical reaction is infinitely fast with respect to gas-phase transport, thus confining chemical reaction to an infinitesimally thin sheet. The assumptions used in this derivation are shown in Table 1.

Figure 1 (a) Schematic diagram of classical d2-law droplet combustion model. (b) Relaxations in the d2-law assumptions.
Table1 Assumptions incorporated into the d2-law of droplet combustion.
| Spherical symmetry. | |
| Isolated droplet in infinite medium. | |
| Isobaric process. | |
| Chemical reaction infinitely fast with respect to diffusion. | |
| Constant gas phase transport properties and heat capacity. | |
| Gas phase quasi-steadiness. | |
| Constant, uniform droplet temperature (No droplet heating). | |
| Neglects Soret effect, Dufour effect and radiation. | |
Unity Lewis number for all gaseous species 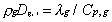
| |
| Negligible buoyancy. | |
| Negligible radiation. |
In this geometrical configuration, fuel vaporizes at the droplet surface and diffuses outward while oxidizer diffuses inward from the ambient environment. The fuel and oxidizer react stoichiometrically, resulting in a zone of intense reaction (i.e. a non-premixed flame). Heat is transported via conduction and radiation outward from the flame to infinity and inward back to the droplet surface. The heat deposited at the droplet surface is balanced by the evaporation process at the vapor/liquid interface. The "classical" d2-law for droplet combustion was first formulated in the 1950s by assuming that gas-phase chemical reaction is infinitely fast with respect to gas-phase transport, thus confining chemical reaction to an infinitesimally thin sheet.
The d2-law theory predicts that the droplet burning rate, flame stand-off position, and flame temperature remain constant throughout the droplet burning lifetime, and are described by the following equations:
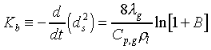 (2.)
(2.)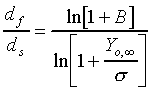 and,
(3.)
and,
(3.)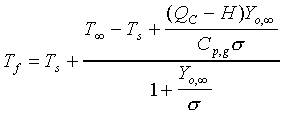
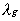 the thermal conductivity of the
gas, Cp,g the specific heat of the gas,
the thermal conductivity of the
gas, Cp,g the specific heat of the gas, 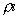 the
liquid density, and B the Spalding transfer number, df
the flame diameter, Yo, is the ambient oxygen mass
fraction, the stoichiometric oxidizer to fuel mass ratio, Tf
the flame temperature, T is the ambient temperature, Ts
the droplet surface temperature, QC the heat of combustion
of the liquid fuel, and H the effective latent heat of vaporization.
The Spalding transfer number, B, is a non-dimensional thermodynamic
parameter measuring the ratio of drive toward vaporization through
the heat of combustion (along with the sensible enthalpy difference
between the ambient environment and the droplet surface), divided
by the resistance to vaporization through the heat of vaporization:
the
liquid density, and B the Spalding transfer number, df
the flame diameter, Yo, is the ambient oxygen mass
fraction, the stoichiometric oxidizer to fuel mass ratio, Tf
the flame temperature, T is the ambient temperature, Ts
the droplet surface temperature, QC the heat of combustion
of the liquid fuel, and H the effective latent heat of vaporization.
The Spalding transfer number, B, is a non-dimensional thermodynamic
parameter measuring the ratio of drive toward vaporization through
the heat of combustion (along with the sensible enthalpy difference
between the ambient environment and the droplet surface), divided
by the resistance to vaporization through the heat of vaporization:
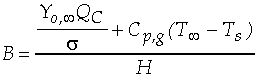
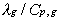 and decreases with increasing
and decreases with increasing
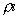 . Quantitative agreement between experiment
and equation 1 can also be achieved provided that appropriate
selections (generally not those determined by the actual physical
values) of transport properties are made. The flame temperature
predicted by equation 3 is, essentially, the adiabatic flame temperature
of the given fuel-oxidizer system assuming no dissociation or
finite flame thickness. Quantitative agreement, in this case,
can be obtained by assuming a suitably enhanced specific heat
to account for deficiencies. The flame stand-off ratio, which
under some experimental conditions can approach a constant value,
is vastly over-predicted under all circumstances by equation 2.
That the quantitative agreement is much worse for the flame position
than for the burning rate is easily explained. The assumptions
incorporated into the d2-law analysis yield a flame
position which is virtually independent of thermal/transport parameters
(generally, Cp,g(T -Ts) <<
. Quantitative agreement between experiment
and equation 1 can also be achieved provided that appropriate
selections (generally not those determined by the actual physical
values) of transport properties are made. The flame temperature
predicted by equation 3 is, essentially, the adiabatic flame temperature
of the given fuel-oxidizer system assuming no dissociation or
finite flame thickness. Quantitative agreement, in this case,
can be obtained by assuming a suitably enhanced specific heat
to account for deficiencies. The flame stand-off ratio, which
under some experimental conditions can approach a constant value,
is vastly over-predicted under all circumstances by equation 2.
That the quantitative agreement is much worse for the flame position
than for the burning rate is easily explained. The assumptions
incorporated into the d2-law analysis yield a flame
position which is virtually independent of thermal/transport parameters
(generally, Cp,g(T -Ts) << 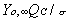 ).
Thus, there are no parameters to choose to obtain quantitative
agreement. In summary, while the d2-law has historically
been shown to be useful in a qualitative sense, it cannot simultaneously
predict the burning rate, flame position and flame temperature.
).
Thus, there are no parameters to choose to obtain quantitative
agreement. In summary, while the d2-law has historically
been shown to be useful in a qualitative sense, it cannot simultaneously
predict the burning rate, flame position and flame temperature.
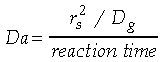
 Spherically
Symmetric Experiments
Spherically
Symmetric Experiments 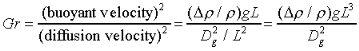
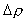 is the characteristic density change,
is the characteristic density change,
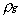 is the mean density, g is the local acceleration
due to gravity, L the characteristic length scale (in this case
the drop diameter), and Dg the mass diffusivity. Similarly,
the Richardson number can be thought of as a comparison
between the characteristic buoyant velocity to the characteristic
convection velocity:
is the mean density, g is the local acceleration
due to gravity, L the characteristic length scale (in this case
the drop diameter), and Dg the mass diffusivity. Similarly,
the Richardson number can be thought of as a comparison
between the characteristic buoyant velocity to the characteristic
convection velocity:
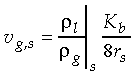
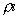 the liquid density, and
the liquid density, and 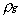 the gas density at
the vapor/liquid interface. For example, the combustion of a 1
mm methanol droplet in air, yields a Stephan flow velocity at
the droplet surface of about 0.16 m/s. At these conditions,
the gas density at
the vapor/liquid interface. For example, the combustion of a 1
mm methanol droplet in air, yields a Stephan flow velocity at
the droplet surface of about 0.16 m/s. At these conditions, 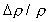 is approximately unity, such that the Richardson number is approximately
0.01, even at normal gravity. This suggests that near the droplet
surface the gas phase is spherically symmetric. However, the gas
phase conservation of mass requires that
is approximately unity, such that the Richardson number is approximately
0.01, even at normal gravity. This suggests that near the droplet
surface the gas phase is spherically symmetric. However, the gas
phase conservation of mass requires that 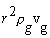 = constant, such that the Stephan flow velocity decays quickly
at increasing gas-phase radii.
= constant, such that the Stephan flow velocity decays quickly
at increasing gas-phase radii.
Microgravity Facility Gravity Level Test Duration Drop tower 10-4 g - 10-6 g 1 - 10 seconds Parabolic flight aircraft 10-1 g - 10-3 g 5 - 15 seconds Sounding rockets 10-4 g 200 - 900 seconds Orbiting spacecraft 10-6 g 1000 - 10000 seconds
Based on the above Grashof number argument, for droplet sizes on the order of 1 millimeter and larger should only be accurate when conducted in drop towers or aboard orbiting spacecraft. The inherent complexity and uncertainty (a typical success rate of about 33% is standard for untethered experiments) of isolated droplet combustion experiments presents difficulties in performing these experiments in sounding rockets. In parabolic flight aircraft, the g-levels are too high to perform isolated droplet combustion experiments with accuracy; however, it is a very good means to test experimental operating systems and procedures.
It is also possible to reduce the effects of buoyancy by conducting experiments in normal gravity at reduced pressure and/or reduced initial droplet size. However, all droplet combustion experiments conducted under normal gravity are complicated by buoyancy and/or intrusion of a suspension device. Buoyancy enhances the gas phase heat and mass transport thereby increasing the burning rate. Since the flame shape is distorted, it is difficult, if not meaningless to define a flame position. Finally, there is an inherent effect of pressure on the chemical kinetics occurring in the flame structure. Since the effects of buoyancy vary with the droplet diameter, normal gravity experiments are completely transient. The presence of a suspension device, meanwhile, distorts the droplet shape and is an additional source of heat loss from the flame.

http://www.princeton.edu/~fldryer/nasa.dir/background.htm
Last updated: April 18, 1997