About Me

Current Position
I am an Assistant Professor of Digital Earth Sciences in the Department of Geological Sciences and Geological Engineering, Queen's University, Canada. I was an associate research scholar in the Department of Geosciences, Princeton University, US. I worked in the Theoretical & Computational Seismology group with Professor Jeroen Tromp.Academic Background
I received a PhD in geophysics from the University of Oslo and NORSAR, Norway, and an MSc in earthquake engineering from the University of Tokyo, Japan. I hold a B.E. in civil engineering and an I.E. in mechanical engineering both with the highest honor from the Tribhuvan University, Nepal.Research Interests
My research area encompasses applied mathematics and computational (geo)mechanics, including (an)elastic-gravitational wave propagation, coseismic deformation and post-earthquake relaxation, glacial isostatic adjustment, gravity/magnetic anomalies, microearthquakes; and hexahedral meshing and scientific visualization. I have (co)developed a number of sophisticated and versatile software packages to solve the problems in those areas.Other Interests
I have a passion for teaching. I received the best lecturer award during my short stint as a lecturer of Civil Engineering immediately after finishing my Bachelor's degree.Hiking in nature with family is my favorite weekend activity.
Research
Spectral-infinite-element Method
The spectral-infinite-element method combines the highly accurate spectral-element method with the mapped-infinite element method to solve the unbounded problems efficiently and accurately. Spectral elements represent the domain of interest, and a single layer of infinite elements captures outer space. To solve the weak form of the unbounded equation, we use Gauss-Legendre-Lobatto quadrature in spectral elements inside the domain of interest. Outside the domain, we use Gauss-Radau quadrature in the infinite direction, and Gauss-Legendre-Lobatto quadrature in the other directions.
The software package SPECFEM-X based on the SIEM aims to solve most (global) quasistatic problems.
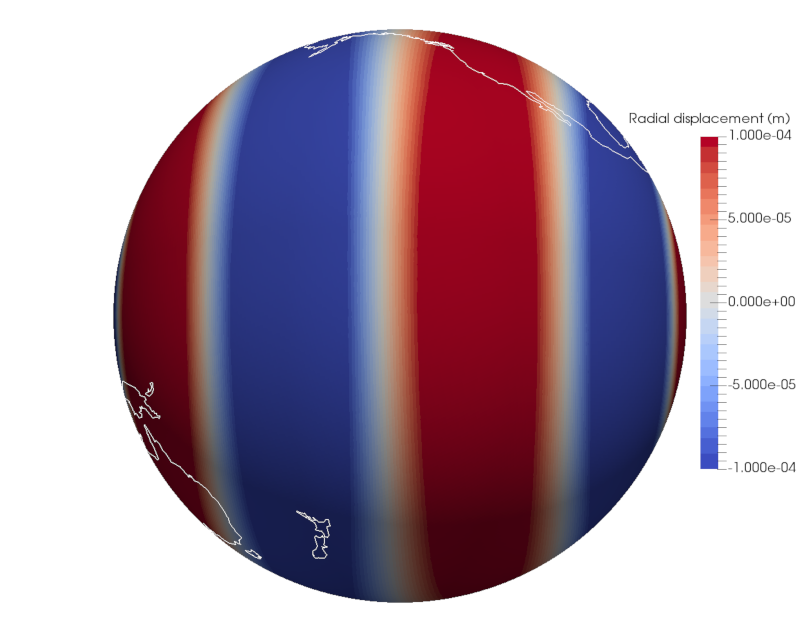
Earthquake-Induced Gravity Perturbation
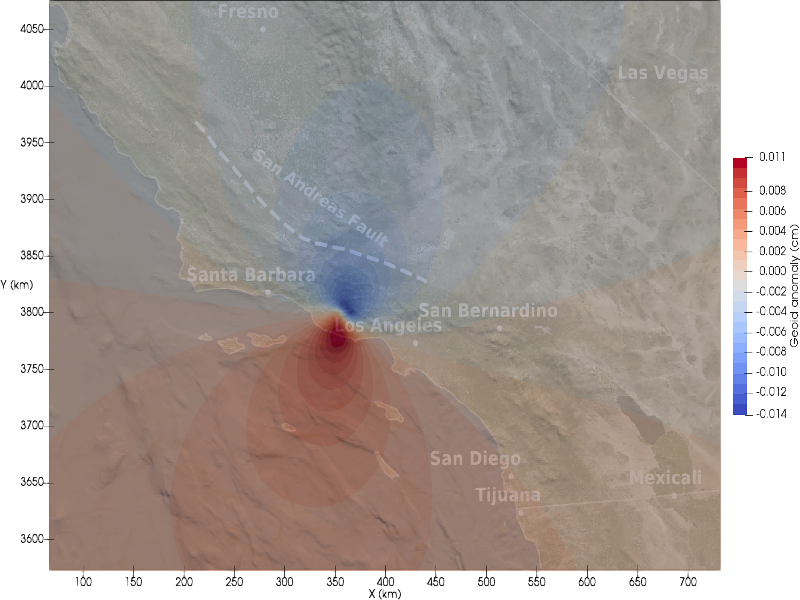
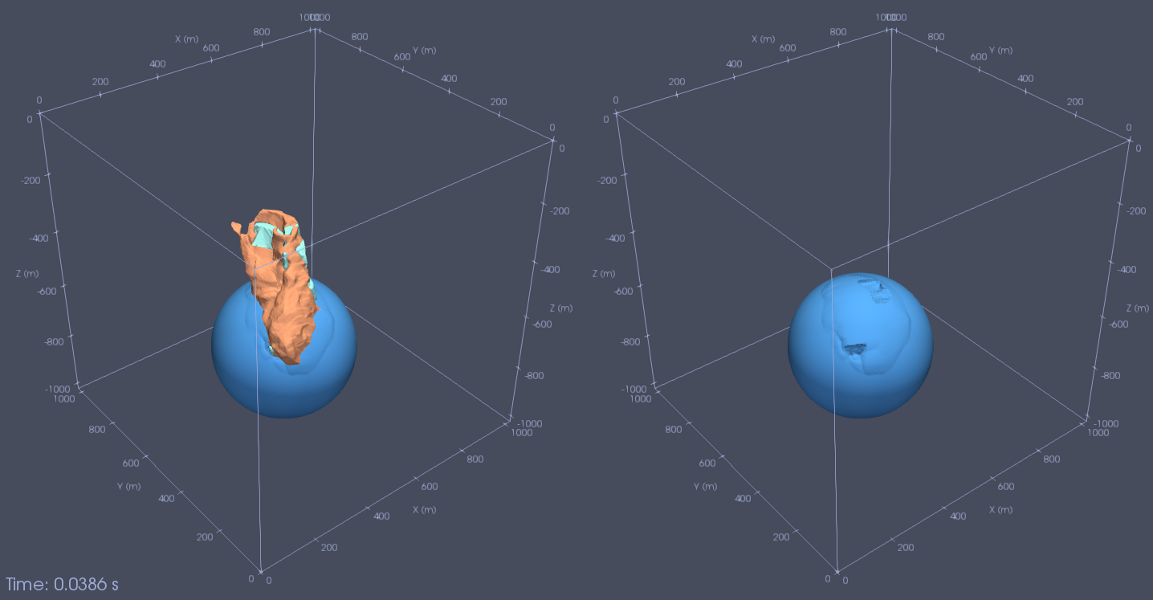
Although earthquake-induced gravity perturbations are frequently observed, numerical modeling of this phenomenon has remained a challenge. Due to the lack of reliable and versatile numerical tools, induced-gravity data have not been fully exploited to constrain earthquake source parameters. From a numerical perspective, the main challenge stems from the unbounded Poisson/Laplace equation that governs gravity perturbations. Additionally, the Poisson/Laplace equation must be coupled with the equation of conservation of linear momentum that governs particle displacement in the solid. Most existing methods either solve the coupled equations in a fully spherical harmonic representation, which requires models to be (nearly) spherically symmetric, or they solve the Poisson/Laplace equation in the spherical harmonics domain and the momentum equation in a discretized domain, a strategy that compromises accuracy and efficiency. We present a spectral-infinite-element approach that combines the highly accurate and efficient spectral-element method with a mapped-infinite-element method capable of mimicking an infinite domain without adding significant memory or computational costs. We solve the complete coupled momentum-gravitational equations in a fully discretized domain, enabling us to accommodate complex realistic models without compromising accuracy or efficiency. We present several coseismic and post-earthquake examples and benchmark the coseismic examples against the Okubo analytical solutions. Finally, we consider gravity perturbations induced by the 1994 Northridge earthquake in a 3D model of Southern California. The examples show that our method is very accurate and efficient, and that it is stable for post-earthquake simulations.
Automated Microearthquake Location
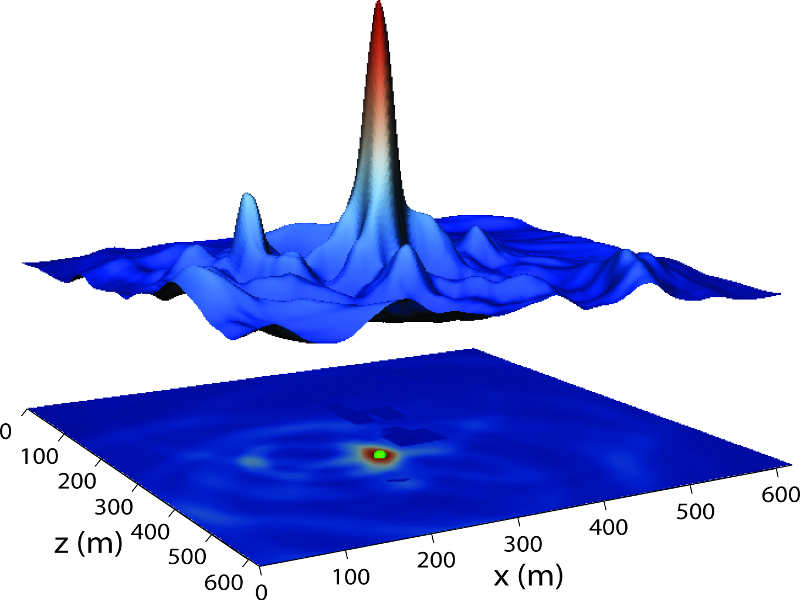
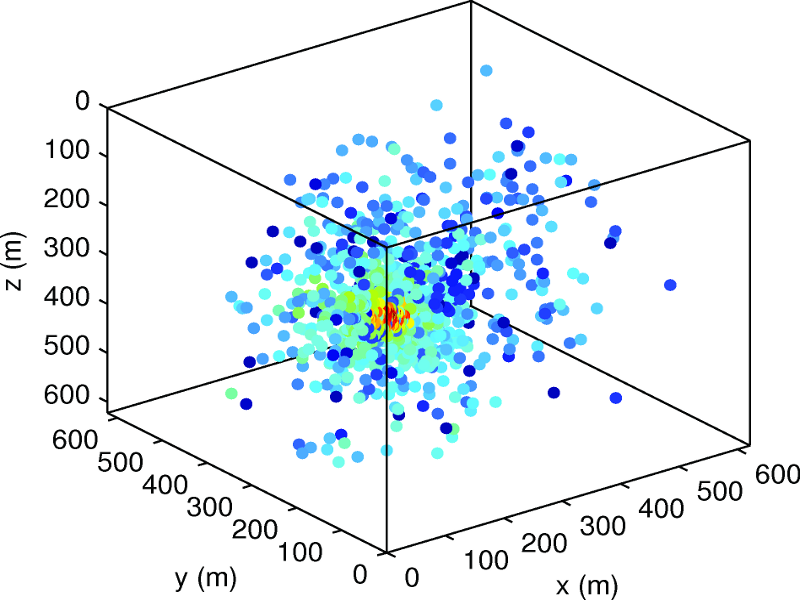
Most earthquake location methods require phase identification and arrival-time measurements. These methods are generally fast and efficient but not always applicable to microearthquake data with low signal-to-noise ratios because the phase identification might be very difficult. The migration-based source location methods, which do not require an explicit phase identification, are often more suitable for such noisy data. Whereas some existing migration-based methods are computationally intensive, others are limited to a certain type of data or make use of only a particular phase of the signal. We have developed a migration-based source location method especially applicable to data with relatively low signal-to-noise ratios. We projected seismograms on to the ray coordinate system for each potential source-receiver configuration and subsequently computed their envelopes. The envelopes were time shifted according to synthetic P- and S-wave arrival times (computed using an eikonal solver) and stacked for a predefined time window centered on the arrival time of the corresponding phase. This was done for each component and phase individually, and the squared sum of the stacks was defined as the objective function. We applied a robust global optimization routine called differential evolution to maximize the objective function and thereby locate the seismic event. Our source location method provides a complete algorithm with only a few control parameters, making it suitable for automatic processing. We applied this method to single and multicomponent data using P and/or S phases. We conducted controlled tests using synthetic seismograms contaminated with a minimum of 30% white noise. The synthetic data were computed for a complex and heterogeneous model of the Pyhäsalmi ore mine in Finland. We also successfully applied the method to real seismic data recorded with the in-mine seismic network of the Pyhäsalmi mine.
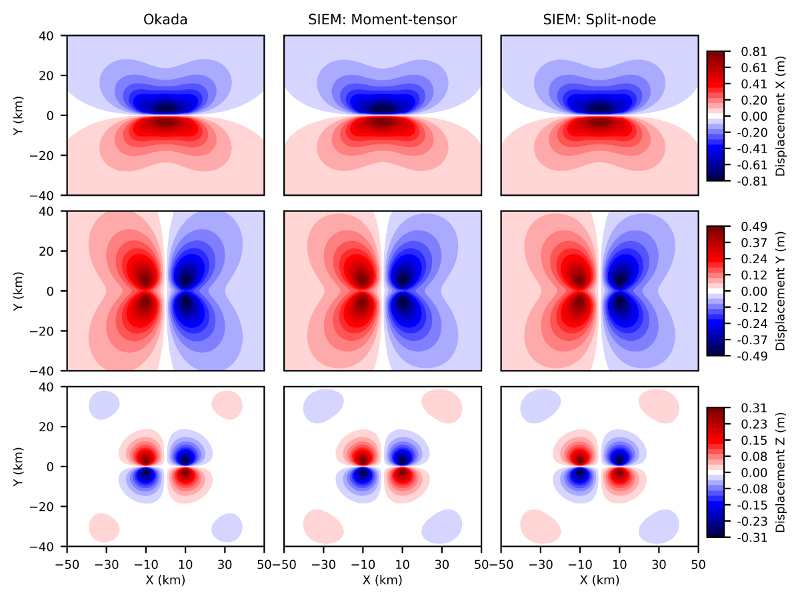
Coseismic Deformation & Post-earthquake Relaxation
Accurate and efficient simulations of coseismic and post-earthquake deformation are important for proper inferences of earthquake source parameters and subsurface structure. These simulations are often performed using a truncated halfspace model with approximate boundary conditions. The use of such boundary conditions introduces inaccuracies unless a sufficiently large model is used, which greatly increases the computational cost. To solve this problem, we develop a new approach by combining the spectral-element method with the mapped infinite-element method. In this approach, we still use a truncated model domain, but add a single outer layer of infinite elements. While the spectral elements capture the domain, the infinite elements capture the far-field boundary conditions. The additional computational cost due to the extra layer of infinite elements is insignificant. Numerical integration is performed via Gauss-Legendre-Lobatto and Gauss-Radau quadrature in the spectral and infinite elements, respectively. We implement an equivalent moment-density tensor approach and a split-node approach for the earthquake source, and discuss the advantages of each method. For post-earthquake deformation, we implement a general Maxwell rheology using a second-order accurate and unconditionally stable recurrence algorithm. We benchmark our results with the Okada analytical solutions for coseismic deformation, and with the Savage & Prescott analytical solution and the PyLith finite-element code for post-earthquake deformation.
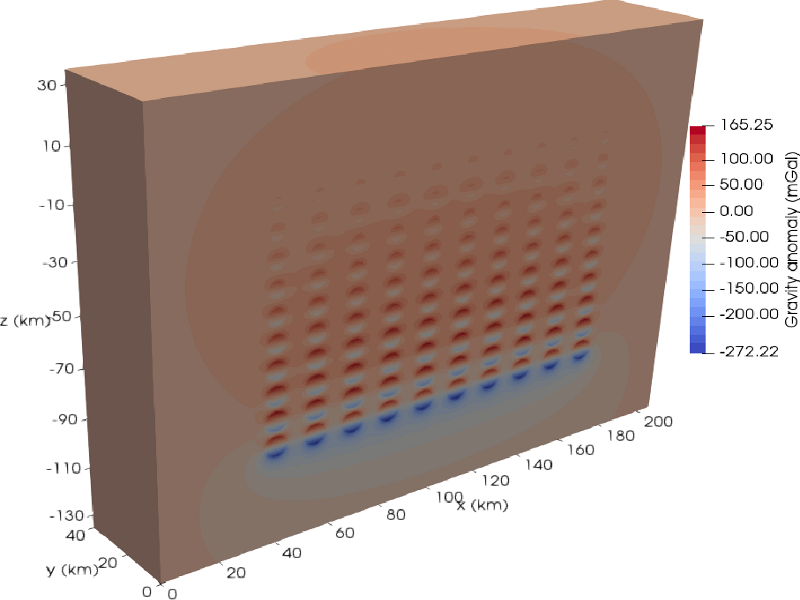
Gravity Anomalies
Gravity anomalies induced by density heterogeneities are governed by Poisson’s equation. Most existing methods for modelling such anomalies rely on its integral solution. In this approach, for each observation point, an integral over the entire density distribution needs to be carried out, and the computational cost is proportional to the number of observation points. Frequently, such methods are sensitive to high density contrasts due to inaccurate resolution of the volume integral. We introduce a new approach which directly solves a discretized form of the Poisson/Laplace equation. The main challenge in our approach involves the unbounded nature of the problem, because the potential exists in all of space. To circumvent this challenge, we combine a mapped infinite-element approach with a spectral-element method. Spectral elements represent the domain of interest, and a single layer of infinite elements captures outer space. To solve the weak form of the Poisson/Laplace equation, we use Gauss–Legendre–Lobatto (GLL) quadrature in spectral elements inside the domain of interest. Outside the domain, we use Gauss–Radau quadrature in the infinite direction, and GLL quadrature in the other directions. We illustrate the efficiency and accuracy of our method by comparing calculated gravity anomalies for various density heterogeneities with corresponding analytical solutions. Finally, we consider a complex 3-D model of an ore mine, which consists of both positive and negative density anomalies.
Magnetic Anomalies
Magnetic anomalies induced by a magnetization distribution are governed by Poisson’s equation. Analogous to gravity anomalies, magnetic anomalies are frequently computed using a direct integral approach, involving an integral over the entire magnetization distribution for each observation point. Alternatively, magnetic anomalies can be computed using the so-called Poisson’s relation, in which the magnetic scalar potential is approximated by the derivative of the gravitational potential based on the analogy between the gravity and magnetic fields. However, this analogy is generally limited to simple isolated objects, and computing the magnetic field involves the second derivative of the gravitational potential. Both methods suffer from an often inaccurate volume integral over complex objects, and the computational cost scales with the number of observation points. We implement a spectral-infinite-element method to directly solve a discretized form of the Poisson/Laplace equation for magnetic anomalies. The spectral-infinite-element method combines the highly accurate spectral-element method with the mapped-infinite element method, which reproduces an unbounded domain accurately and efficiently. This combination is made possible by coupling Gauss-Legendre-Lobatto quadrature in spectral-elements with Gauss-Radau quadrature in infinite elements along the infinite directions. We illustrate the efficiency and accuracy of our method by comparing calculated magnetic anomalies for various magnetization heterogeneities with corresponding analytical and commonly used computational solutions. Finally, we consider a practical example involving a complex 3D model of an ore mine.
Multistage Excavation
We implement a 3D spectral-element method for multistage excavation problems. To simulate excavation in elastoplastic soils, we employ a Mohr–Coulomb yield criterion using an initial strain method. We parallelize the software based on non-overlapping domain decomposition using MPI. We verify the uniqueness principle for multistage excavation in linear elastic materials. We validate our serial and parallel programs, and illustrate several examples of multistage excavation in elastoplastic materials. Finally, we apply our software to a model of the Pyhäsalmi ore mine in Finland. Strong-scaling performance tests involving multistage excavation show that the parallel program performs reasonably well for large-scale problems.
Slope Stability
We implement a spectral‐element method for 3D time‐independent elastoplastic problems in geomechanics. As a first application, we use the method for slope stability analysis ranging from small to large scales. The implementation employs an element‐by‐element preconditioned conjugate‐gradient solver for efficient storage. The program accommodates material heterogeneity and complex topography. Either simple or complex water table profiles may be used to assess effects of hydrostatic pressure. Both surface loading and pseudostatic seismic loading are implemented. For elastoplastic behavior of slopes to be simulated, a Mohr–Coulomb yield criterion is employed using an initial strain method (i.e., a viscoplastic algorithm). For large‐scale problems, the software is parallelized on the basis of domain decomposition using Message Passing Interface. Strong‐scaling measurements demonstrate that the parallelized software performs efficiently. We validate our spectral‐element results against several other methods and apply the technique to simulate failure of an earthen embankment and a mountain slope.
Publications
Reviewed Articles
- Jeong, C., Manalaysay, A., Gharti, H. N., Guan, S., and Vignola, J., 2019. Applicability of 3D spectral element method for computing close-range underwater
piling noises,
Journal of Theoretical and Computational Acoustics. DOI:10.1142/S2591728519500129. - Gharti, H. N. and Tromp, J., 2019. Spectral-infinite-element simulations of magnetic anomalies,
Geophysical Journal International, 217, 1656-1667. DOI:10.1093/gji/ggz107. - Langer, L., Gharti, H. N., and Tromp, J., 2019. Impact of topography and three-dimensional heterogeneity
on coseismic deformation,
Geophysical Journal International, 217, 866-878. DOI:10.1093/gji/ggz060. - Gharti, H. N., Langer, L., and Tromp, J., 2019. Spectral-infinite-element simulations of earthquake-induced
gravity perturbations,
Geophysical Journal International, 217, 451-468. DOI:10.1093/gji/ggz028. - Vaaland, U. B., Gharti, H. N., and Tromp, J., 2019. Simulations of seismic wave propagation using a spectral-element
method in a Lagrangian framework with logarithmic strain,
Geophysical Journal International, 216, 2148-2157. DOI:10.1093/gji/ggy546. - Wang, N., Li, J., Borisov, D., Gharti, H. N., Shen, Y., Zhang, W., and Savage, B., 2019. Modeling three-dimensional wave propagation in anelastic models with
surface topography by the optimal strong stability preserving Runge-Kutta method,
Journal of Geophysical Research - Solid Earth, 124. DOI:10.1029/2018JB016175. - Gharti, H. N., Langer, L., and Tromp, J., 2019. Spectral-infinite-element simulations of coseismic and
post-earthquake deformation,
Geophysical Journal International, 216, 1364-1393. DOI:10.1093/gji/ggy495. - Gharti, H. N., Tromp, J., and Zampini, S, 2018. Spectral-infinite-element simulations of gravity anomalies,
Geophysical Journal International, 215, 1098-1117. DOI:10.1093/gji/ggy324. - Lloyd, S. F., Jeong, C., Gharti, H. N., Vignola, J., and Tromp, J., 2018. Spectral-element simulations of acoustic waves induced by a moving underwater source,
Journal of Theoretical and Computational Acoustics. DOI:10.1142/S2591728518500408. - Paap, B., Kraaijpoel, D., Bakker, M., and Gharti, H. N., 2018. Wave propagation modelling of induced earthquakes at the Groningen gas production site,
Geophysical Journal International, 214, 1947-1960. DOI:10.1093/gji/ggy225 - Lecomte, I., Lubrano-Lavadera, P., Wuestefeld, A., Kaschwich, T., Albaric, J., and Gharti, H. N., 2015. Focusing in migration-based location of weak microseismicity: modelling point-spread function for resolution analyses,
SEG Technical Program Expanded Abstracts, 2491-2495. DOI:10.1190/segam2015-5813282.1. - Gharti, H. N., Oye, V., Komatitsch, D., and Tromp, J., 2012. Simulation of multistage excavation based on a
3D spectral-element method,
Computers & Structures, 100–101, 54–69. DOI:10.1016/j.compstruc.2012.03.005 - Gharti, H. N., Komatitsch, D., Oye, V., Martin, R., and Tromp, J., 2012. Application of an elastoplastic spectral-
element method to 3D slope stability analysis,
International Journal for Numerical Methods in Engineering, 91, 1–26. DOI:10.1002/nme.3374 - Gharti, H. N.; Oye, V.; Kühn, D., and Zhao, P., 2011. Simultaneous microearthquake location and moment-tensor estimation using time-reversal imaging,
SEG Technical Program Expanded Abstracts, 30, 1632-1637. DOI:10.1190/1.3627516 - Gharti, H. N.; Oye, V.; Roth, M., and Kühn, D., 2010. Automated microearthquake location using envelope stacking and robust global optimization,
Geophysics, 75, MA27-MA46. DOI:10.1190/1.3432784. - Oye, V., Gharti, H. N., Aker, E., and Kühn, D., 2010. Moment tensor analysis and comparison of
acoustic emission data with synthetic data from spectral element method,
SEG Technical Program Expanded Abstracts,29(1):2105–9. DOI:10.1190/1.3513260. - Kühn, D., Gharti, H. N., Oye, V., and Roth, M., 2009, Analysis of mining-induced seismicity using focal mechanism and waveform computations in heterogeneous media.
EAGE extended abstracts, Amsterdam. DOI:10.3997/2214-4609.201400028 - Gharti, H. N., Oye, V., and Roth, M., 2008. Travel times and waveforms of microseismic data in
heterogeneous media,
SEG Tech Prog Expanded Abstracts, 27(1):1337–41. DOI:10.1190/1.3059162.
Other Articles
- Gharti, H. N., Komatitsch, D., Langer, L., Martin, R., Oye, V., Tromp, J., Vaaland, U., and Yan, Z., 2017. SPECFEM 3D Geotech: an open-source, parallel and cross-platform geotechnical engineering application (Version v1.2.0),
Zenodo. DOI:10.5281/zenodo.820154 - Gharti, H. N., Langer, L., Roth, M., Tromp, J., Vaaland, U., and Yan, Z., 2017. MeshAssist: an open-source and
cross-platform meshing assistant tool,
Zenodo. DOI:10.5281/zenodo.883448 - Gharti, H. N., and Tromp, J., 2017. A spectral-infinite-element solution of Poisson’s equation: an application to
self gravity.
arXiv:1706.00855. - Gharti, H. N., Oye, V., Roth, M., and Kühn, D., 2017. Wave propagation modelling in various microearthquake environments using a spectral-element method.
arXiv:1706.05217
Conferences Presentations
- Gharti, H. N., Langer, L., Simons, F. J., Tromp, J, and Zampini, S., 2018. Spectral-Infinite-Element Simulation of Potential Field Problems in Geophysics,
AGU Fall Meeting Abstracts, DI24B-14. - Langer, L., Gharti, H. N., and Tromp, J, 2017. Investigating the Importance of 3D Structure & Topography in Seismic Deformation Modeling: Case Study of the April 2015 Nepal Earthquake,
AGU Fall Meeting Abstracts, G43A-0915. - Manalaysay, A., Jeong, C., and Gharti, H. N., 2017. High-resolution spectral-element computation of underwater noises due to offshore piling,
The Journal of the Acoustical Society of America, 142, 2686. DOI:10.1121/1.5014798 - Lloyd, S., Jeong, C, Gharti, H. N., and Tromp, J., 2017. Computation of acoustic wave responses due to moving underwater acoustic sources in complex underwater environments using a spectral element method,
The Journal of the Acoustical Society of America, 141, 3531. DOI:10.1121/1.4987453 - Gharti, H. N., and Tromp, J, 2015. Spectral-infinite-element Simulations of Self-gravitating Seismic Wave Propagation,
AGU Fall Meeting Abstracts, S13C-04. - Langer, L., Gharti, H. N., and Tromp, J, 2016. Investigating the Importance of 3D Structure in Seismic Deformation Modeling,
AGU Fall Meeting Abstracts, G51B-1104. - Wang, N., Li, J., Borisov, D., Gharti, H. N., Shen, Y., Zhang, W., Savage, and B. K., 2016. Three-dimensional wave field modeling by a collocated-grid finite-difference method in the anelastic model with surface topography,
AGU Fall Meeting Abstracts, S23C-2781. -
Kühn, D., Vavrycuk, V., Aker, E., Gharti, H. N., Oye, V., and Huynh, K., 2013, Source Mechanisms of Acoustic Emissions due to Failure Around a Borehole in a Triaxial Lab Experiment,
4th EAGE Passive Seismic Workshop. DOI:10.3997/2214-4609.20142348 - Gharti, H. N., Austermann, J., Komatitsch, D., Lau, H., Mitrovica, J. X., Peter, P., Tromp, J., Xie, Z., and Zampini, S., 2013. Efficient Numerical Solution of Global Dynamic and Quasistatic Problems Using a Spectral-Element Method Coupled with an Infinite-Element Approach,
AGU Fall Meeting Abstracts, DI34B-03. - Gharti, H. N., Oye, V., and Roth, M., 2009. Automated Event Location for Noisy Microearthquake Data Using Envelope Stacking and Robust Global Optimization,
AGU Fall Meeting Abstracts, S32B-04. -
Kühn, D., Gharti, H. N., Oye, V., and Roth, M., 2009. Analysis of Mining-induced Seismicity Using Focal Mechanism and Waveform Computations in Heterogeneous Media,
71st EAGE Conference and Exhibition incorporating SPE EUROPEC 2009. DOI:10.3997/2214-4609.201400028 -
Kühn, D., Gharti, H. N., Oye, V., and Roth, M., 2009, Microseismic Deformation Rate Monitoring,
Second EAGE Passive Seismic Workshop - Exploration and Monitoring Applications 2009. DOI:10.3997/2214-4609.20146744 -
Kühn, D., Gharti, H. N., Oye, V., Roth, M., 2009, Automatic determination of full moment tensor solution from P-wave first motion amplitudes,
Second EAGE Passive Seismic Workshop - Exploration and Monitoring Applications 2009. DOI:10.3997/2214-4609.20146731 - Oye, V. and Gharti, H. N., 2009. Location of Microearthquakes in Various Noisy Environments Using Envelope Stacking,
AGU Fall Meeting Abstracts, S23B-1751.
Please visit my Google Scholar and/or ResearchGate profile for more detailed publication list.
Software
I have (co)developed a number of software packages for engineering and geoscientific applications for research and class lectures. Depending on the requirements and the applications, I mostly use Fortran 2008, C, C++, Python, Matlab, and Mathematica.
SPECFEM-X

SPECFEM-X is a versatile and unified upcoming software package. It aims to solve many (global) quasistatic and geodynamics problems.
Major features:
- Coseismic and post-earthquake deformation
- Earthquake-induced gravity perturbation
- Gravity anomalies
- Magnetic anomalies
- Generalized viscoelastic rheology
- Glacial isostatic adjustment
- Slow slip events
- Thermomechanical simulations
- Generalized source implementation
- Builtin and externally ported solvers
- Parallelization based on the MPI and domain decomposition
SPECFEM 3D Geotech

SPECFEM 3D Geotech is an open-source command-driven software for 3D slope stability analysis and simulation of 3D multistage excavation based on the spectral-element method. The software can run on a single processor as well as multi-core machines or large clusters. It is written mainly in FORTRAN 90 and parallelized using MPI based on domain decomposition. The element-by-element preconditioned conjugate-gradient method is implemented to solve the linear equations. For elastoplastic failure, a Mohr-coulomb failure criterion is used with a viscoplastic strain method. This program does not automatically determine the factor of safety of slope stability. Simulations can be performed for a series of safety factors. After plotting the safety factor versus maximum displacement curve, one can determine the factor of safety of the given slope. Although the software is optimized for slope stability analysis and multistage excavation, other relevant simulations of quasistatic problems in solid (geo)mechanics can also be performed with this software.
Major features:
- Elastoplastic failure
- Parallelization based on the MPI and domain decomposition
- Slope stability analysis
- Multistage excavation
- Ground water table
- Crossplatform compatibility
- Element-by-element solver
MeshAssist

MeshAssist is a collection of tools which assists meshing of complex and realistic 2D/3D models for FEM/SPECFEM simulations. As its name suggests, it is NOT a meshing software. It is only a meshing assistant!
Major features:
- Convert complex geological surfaces to meshable ACIS surface
- Convert vector graphics to ACIS geometry
- Convert AUTOCAD files to ACIS geometry
- Convert DEM or XYZ data to ParaView and CUBIT/Trelis files
- Several functions for 1D/2D/3D geometry data
- Convert Exodus mesh files to SPECFEM(-X) files
Please visit my GitHub profile for more detailed list of my software contributions.
News and Media
March 09, 2017
CIG Webinar
Hom Nath Gharti gave a CIG webinar talk on "Introduction to the Spectral-Infinite-Element Method" on March 09, 2017.