Computational imaging

In traditional imaging, one tries to create a perfect image directly. In computational imaging, a distortion is added to the optical path, so that the recorded picture no longer resembles the object. Since the distortion is known, however, an image can be reconstructed numerically. This a priori information can be used to obtain "extra" information about the object, such as increased resolution and depth. We have generalized computational imaging to include nonlinear dynamics and are applying it to super-resolution microscopy, phase retrieval, and biomedical imaging.
Physics-informed machine learning
Modern machine learning algorithms are based on pattern matching, with connections providing correlations between the output and input. In many cases, such as graphics and entertainment, the output simply has to look right. In other cases, such as scientific and medical applications, the output actually has to be right. We are developing imaging, analysis, and prediction algorithms to ensure this, with physical conservation laws and mathematical symmetries built into the networks themselves.
Machine learning for COVID-19
We design AI systems that examine patient data holistically, e.g. chest x-rays and ultrasound, radiology reports, and blood tests. Hypergraph networks analyze the different data types (images, text, and numbers) on an equal footing, while attention-focusing algorithms scan both global anatomy and local features. The results help physicians categorize patient triage, treatment, and outcome.
Biomedical ultrasound
Ultrasound operates like radar, with a probe beam sent to the object and an echo recorded. In the simplest case, the reflected signal is at the same frequency as the probe, and the return signal gives the distance of the object. In more advanced cases, the response is at a different frequency. Measuring these frequencies gives extra information about the sample but is complicated by material properties, scattering, and noise. We are working to overcome these issues, particularly for tissue and biomedical ultrasound.
Microfluidic microscopy
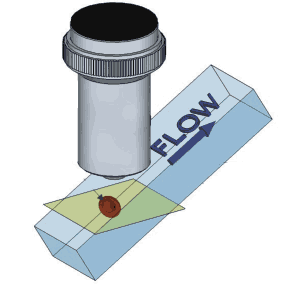
Microfluidics is becoming increasingly useful for transporting and sorting biological objects. In this research, we use the flow as a new degree of freedom for imaging. Examples include tilting the fluid channel for focus at different depths and cell tomography by recording different perspectives. This integrated approach provides high-speed 3D imaging with no mechanical movement of the microscope, minimal stress on the biosamples, and small computational overhead.
Optical hydrodynamics
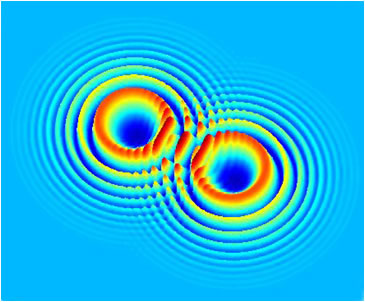
Intuitively, the propagation of light can be considered as the flow of a “fluid” from high-intensity to low-intensity, e.g. a candle illuminating the shadows of a room. Standard fluid behavior, such as flow around objects, shock waves, and turbulence, are all possible with light. New features arise, however, as wave diffraction (rather than viscosity or surface tension) moderates the dynamics. This difference leads to new mathematics and gives insight into both traditional and quantum fluids.
Photonic plasma
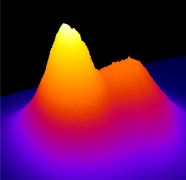
When the light is partially incoherent, then its propagation can be treated as a statistical fluid, i.e. as a plasma. In this photonic plasma, nonlinearity creates an effective plasma frequency, while the finite correlation length creates an effective Debye length. This formalism unifies all previous treatments of nonlinear statistical optics and predicts fundamentally new dynamics for nonlinear light propagation. It also allows observation of phenomena that are difficult, if not impossible, to observe in material plasma.
Photonic lattices
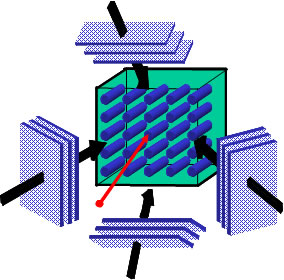
Photonic lattices, e.g. waveguide arrays, facilitate the guiding and control of light. Typically periodic structures, they are difficult tofabricate, especially in a nonlinear medium. We bypass these difficulties by holographically inducing photonic structures in a photorefractive crystal. The waveguides then acquire the nonlinearity of the medium, allowing studies of wave mixing constrained by geometry. Applications include all-optical material modeling, nonlinear spectroscopy, and spectral filtering.
Quantum optics
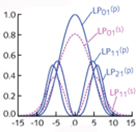
Classical optics treats light as a smooth continuum. Quantum optics introduces new effects, and can surpass classical limits, by exploiting the discrete nature of photons (and their correlations). Historically, quantum optics experiments used single-point detectors and scanning, which limit the possible outcomes and inhibit true quantum imaging. In contrast, we use megapixel cameras that record an entire image at once. The resulting pictures open new applications in quantum sensing, imaging, and information processing.







