Critical Nucleus
Index
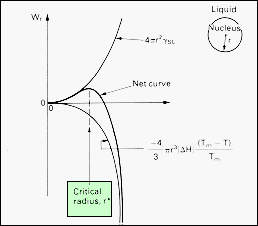
The formation of a second phase involves the interplay of two contributions to the Gibbs function of the system. As the new phase forms, its radius, r, increases, and its surface increases as r2.  The surface energy of the nucleus increases as 4pr2g, where g is the interphase surface energy. The new phase stable below the transformation temperature, so that the volume energy of the nucleus is less than that of the same volume of the initial phase. The volume energy term therefore decreases the Gibbs function of the system as r3. For the nucleus of radius r, the volume energy is - (4/3)pr3(DGV), where DGV is the volume energy decrease upon creating the new phase.

As shown, initially the surface energy dominates the process of nucleation and a nucleus of radius 
r < r* can reduce the Gibbs energy of the system by dissolving ( r -> 0). For r > r* nucleus growth decreases the Gibbs function of the system and is favored. The radius, r*, at which this transition occurs is the critical radius and a nucleus of this radius is a critical nucleus.
From: Ashby and Jones, 
"Engineering Materials 2," 
Pergamon (1986)