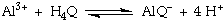
Chemistry:
The reaction of H4Q with Al 3+ is shown below.
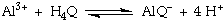
The equilibrium expression for this reaction is
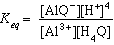(eqn.
1)
To calculate the value of the equilibrium constant you need to express the concentrations in terms that can be measured or calculated from initial conditions. First define the change needed for the system to reach equilibrium. Next define the equilibrium conditions by applying this change to the initial conditions.
| Al3+ | H4Q | AlQ- | H+ | |
|---|---|---|---|---|
| initial | [Al3+]initial |
[H4Q]initial |
0 |
[H+] |
| change | -[AlQ-]eq |
-[AlQ-]eq |
+[AlQ-]eq |
+4[AlQ-]eq |
| equilibrium | [Al3+]initial - [AlQ-]eq |
[H4Q]initial - [AlQ-]eq |
+[AlQ-]eq |
[H+] |
Since 4[AlQ-]eq <<[H+], the equilibrium [H+] is approximately equal to the [H+] of the buffered solution. Now the equilibrium expression becomes
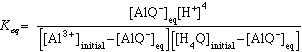(eqn.
2)
Gibbs Free Energy
The Gibbs free energy,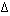 
G°,
can be defined as
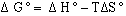(eqn.
3)
where 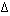H°
and 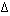S°
are the standard free enthalpy and entropy respectively. It is also
defined as
(eqn.
4)
where R is the gas constant, T is temperature in kelvins, and K is the equilibrium constant. By combining equations 3 and 4 we obtain
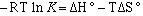(eqn.
5)
or
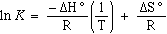(eqn.
6)
and this is an equation for a straight line. Therefore a plot of ln K vs
1/T will give a straight line. From the value of the slope and
intercept you can determine 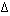H°
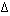and S°.