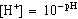 (eqn.
7)
(eqn.
7)Calculations:
To evaluate the equilibrium expression, you need to determine the equilibrium concentration of the reactants and products.
[H+]eq:
Since the solution is buffered at a constant pH, the [H+]
does not change during the reaction. The value of the [H+] eq
will equal [H+] and can be calculated from the pH by
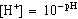 (eqn.
7)
(eqn.
7)
[AlQ-]eq:
The product, AlQ-, absorbs light at 550 nm, and its
concentration is determine from Beer's law. The reactant, H4Q,
does not absorb strongly at this wavelength, and the "blank"
will correct for any absorbance from the H4Q. Beer's law
gives a relationship between the absorbance and concetration.
Explicitly stated Beer's law is
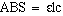 (eqn.
8)
(eqn.
8)
where ABS = absorbance of the solution
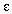 =
extinction coefficient. For AlQ-
=
extinction coefficient. For AlQ- 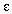 =
25,000 L/mol cm
=
25,000 L/mol cm
l = path length of the cell. In this case l = 0.90 cm
c = equilibrium concetration in moles/L of AlQ-
so [AlQ-]eq is calculated by
 (eqn.
9)
(eqn.
9)
However you recorded the % transmission for your solutions, not the absorbance. Recording the % transmittance is more accurate then recording the absorbance, since the % transmittance scale is linear while the absorbance scale is logrithmic. Therefore the % transmittance is converted to ABS by
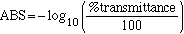 (eqn.
10)
(eqn.
10)
[Al3+]eq: To
calculate this value you first need to determine the [Al3+]initial
value. In this experiment you placed 2 mL of stock [Al3+]
solution in a test tube with 2 mL of stock [H4Q] solution.
The net result is that the Al3+ solution was diluted by1/2.
The initial concetration is not equal to the value on the lable of the
stock reagent bottle. The concetration after a dilution can be
calculated by
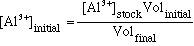 (eqn.
11)
(eqn.
11)
where Volinitial = 2.0 mL and Volfinal = 4.0 mL.(
Remember that during a dilution process, the number of moles of solute
does not change.)
Now [Al3+]eq = [Al3+]initial -
[AlQ-]eq
[H4Q]eq:
This is calculated in a similar method as [Al3+]eq
is calculated, since the same process was use to prepare the solution.
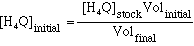 (eqn
12)
(eqn
12)
Volinitial and Volfinal are the same as above. And [H4Q]eq = [H4Q]initial - [AlQ-]eq
You will need to calculate the equilibrium constant at each temperature. You only need to show one sample calculations, and summarize your results in a table.
| T(°C) | % transmittance | ABS | [AlQ-]eq | [Al3+]eq | [H4Q]eq |
| temp. 1 | |||||
| etc. |
Gibbs Free Energy:
For the graph you need values for 1/T and ln K at each temperture reading. Remember that temperature is in kelvins (°C + 273.15). Summarize this data in a table.
| T (kelvins) | 1/T kelvins | K | ln K |
| temp. 1 +273.15 | |||
| etc. |
Draw a graph of ln K vs 1/T following these basic guidelines:
1. use a graphing program (Excel, KaleidaGraph, Cricket graph) or use
good graphing paper.
(see http://www.ncsu.edu/labwrite/res/gt/graphtut-home.html
for a brief into to graphing in Excel)
2. axes should be labeled. Plot the dependent varialble on the y-axis,
and the independent variable on the x-axis.
3. a caption or title explaining what the graph means.
The values of 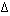 H°
and
H°
and 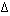 S°
are obtained from the slope and y-intercept of your graph. One method
for determining the slope and y-intercept is to perform a Least Squared
Analysis. This is also refered to as a Linear Regression Analysis or a
Linear Curve Fit. Most graphical calculators or graphing programs are
capable of this analysis. Otherwise you will determine these values
from the graph. The slope is
S°
are obtained from the slope and y-intercept of your graph. One method
for determining the slope and y-intercept is to perform a Least Squared
Analysis. This is also refered to as a Linear Regression Analysis or a
Linear Curve Fit. Most graphical calculators or graphing programs are
capable of this analysis. Otherwise you will determine these values
from the graph. The slope is
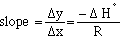 (eqn.
13)
(eqn.
13)
and
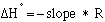 (eqn.
14)
(eqn.
14)
where R is the gas constant. R = 8.3145 J/mol K or 1.987 cal/mol K
The y-intercept, the point of intersection of the line on the y-axis when x=0, is
 (eqn.
15)
(eqn.
15)
and
 (eqn.
16)
(eqn.
16)
There is no uncertainity analysis for this experiment.