Review Problem Set 1

Due Wednesday, 11/6. You may collaborate with other students, provided that you write up answers yourself and identify people you have worked with. These questions are meant to resemble what might go on a final exam, though some of them may take a little longer to answer than would real exam questions. To get the most benefit, you should probably work at the questions on your own first, before consulting with others. The point scores on this exercise will make up 10% of the overall course grade.

1. What are the implications of the standard Solow growth model with Cobb-Douglas technology when ? Is there a steady state value of k? Does the growth rate converge to some limiting value as ?

2. Consider the Solow model with a CES production function, i.e. with

(1)

In this production function we require and , with producing the Cobb-Douglas special case. An interesting fact is that when , not every set of values for the other parameters s,a , n, A, and implies the existence of a steady state with constant .

1. Is it high or low values of s that can produce non-existence of a steady state k?
2. When the steady state doesn't exist, what happens instead? Oscillating k? Constantly growing k? Constantly shrinking k? You might find a diagram, sketching how behaves as a function of k, helpful in answering this question.

[Note that the answers to these two questions may be different according to whether or .]

3. In the Solow model with CES production function we can introduce purely labor-augmenting technical change and still possibly find a steady-state. (We know this because it is true with any linear homogenous production function in the Solow model.) That is, we can replace L in with , and possibly find that the model converges to a steady state in which is constant, under the usual assumption of exogenous population growth at the rate n. On the other hand, this is not in general true if instead we have capital-augmenting technical change, i.e. we replace K in with

1. Show that we do get a steady-state with a constant growth rate of output per worker in the special case (i.e. Cobb-Douglas) when technical change is given by (1). What is the steady-state growth rate of output per worker in this case, as a function of the parameters of the model? [This really replicates what was done in class.]
2. Prove that there cannot be a steady state with constant growth rate of output per worker in the presence of purely capital-augmenting technical change when . [This is quite hard, I think. You might try (linear production function) or (fixed coefficients) first. And even these two cases may take more time and algebra than they are worth. If it looks like it will be impractically hard, write an answer that explains how you would go about it if the algebra weren't so complicated. This is practice for a situation you could face on an exam: your attempt to get a precise answer is fruitless, but you want to get partial credit by showing you know how to go about it in principle.]

4. Consider a two-period life OG model with a distorting tax on capital. That is, we assume as usual that consumers born at t maximize

subject to

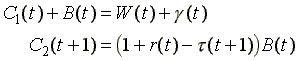The tax is paid by consumers, so the price paid for capital by firms, Q, is still 1+r, despite the existence of the tax. The parameter g is a per capita transfer payment to the young, financed out of the tax on capital. The government budget constraint is

Assume the capital tax rate is fixed at and (as usual) that population grows at the constant rate . Assume also that firms use a Cobb-Douglas technology:

1. Find the steady-state levels of , , and B as functions of the tax rate and of the other parameters of the model.
2. Does the tax on capital have the expected effect of lowering the steady-state capital stock?
3. Can a tax on capital achieve the golden rule equilibrium when the economy would in the absence of taxes be dynamically inefficient?

5. The Solow model is traditionally presented in continuous time. A discrete time version would make the following changes in the equations

Can you derive an expression for steady state capital stock and output per worker in the discrete time version? Does it depend on parameters in the same way as the corresponding continuous time expression?

6. The Solow model assumes a constant rate of savings out of gross output (including depreciation). In the OG model, the savings rate out of gross output varies systematically with the parameters of the model.

1. Determine how the steady state savings rate out of gross output varies with A, b, (the exponent on capital in the Cobb-Douglas technology), a (the exponent on in the utility function), n, and d.
2. Determine how the savings rate varies with initial capital per worker, assuming we begin out of steady state.
3. If we begin out of steady state, with above or below its steady state value, do all the parameters affect the savings rate in the first period in the same direction that they affect the steady state savings rate, as you determined in (i)?

{}