Implications of Magnitude Distribution Comparisons
between Trans-Neptunian Objects and Comets
by
Dr. C. A. Wood, Advisor
December 1, 1995
Implications of Magnitude Distribution Comparisons
between Trans-Neptunian Objects and Comets
Abstract
The population of observed trans-neptunian objects has a fairly well-defined magnitude distribution, however, the population of observed short-period comets does not. This analysis of the population distributions of observed trans-neptunian objects (T NOs) and short-period comets (SPCs) indicates that the observed number of TNOs and SPCs is insufficient to judge conclusively whether the trans-neptunian objects are related to the short-period comets or whether the TNOs are part of the Kuiper belt from w hich the SPCs are believed to be derived. Differences in the population distributions of TNOs and SPCs indicate that the TNOs are not representative of the Kuiper belt as a whole, even if they are part of the Kuiper belt. Further analysis of the populat ion distributions of comets and the TNOs has provided additional information and some predictions about the populations’ characteristics. This derived information includes the facts that: the six brightest SPCs for which H10 magnitudes have be en calculated likely belong to the Oort cloud population (long-period) of comets instead of the Kuiper belt population of comets; Pluto and Charon are likely to belong to the TNO population instead of the major planet population; there are likely to be ~1 09 TNOs in the Kuiper belt, including many Pluto-sized objects, massing a total of ~1025 kg in all.
Introduction
Several unusual objects have been discovered orbiting the Sun beyond the orbit of Neptune. Prior to these discoveries, a disk of cometary bodies, called the Kuiper belt, had been hypothesized to exist beyond the orbit of Neptune. This disk of com etary bodies is believed to be the immediate source of all short-period comets.
The recently discovered trans-neptunian objects are now believed to be the first few members of the hypothesized Kuiper belt of comets to be discovered. I have attempted to judge whether the magnitude distributions of the observed trans-neptunian obje cts and the short-period comets are similar or different enough to state whether the observed trans-neptunian objects are indeed members of the Kuiper belt and whether the observed Kuiper belt is the source of short-period comets.
Descriptions and judgments of the type made herein are important for several reasons: 1) descriptions of observed phenomena are important in and of themselves as information about the universe (and particularly the solar system) in which we live; 2) identification of the observed trans-neptunian objects as members of the Kuiper belt would confirm the Kuiper belt hypothesis; or negative identification could help reject the Kuiper belt hypothesis; 3) descriptions of the TNOs, comets, and the Kuiper belt would help establish their relationship to one another; and 4) information about portions of our solar system, particularly the outermost, least-changed portions, helps to ref ine and develop ideas about how our solar system formed and how it has evolved.
Background
Analysis of the orbital characteristics of comets reveals some interesting features. In particular, the distributions of cometary osculating orbital elements:1 the semimajor axis distribution, orbital eccentricity distribution, and orbi tal inclination distribution of comets, all contain a common feature that is of particular interest; they display an asymmetry that seems to indicate two distinct populations of comets.
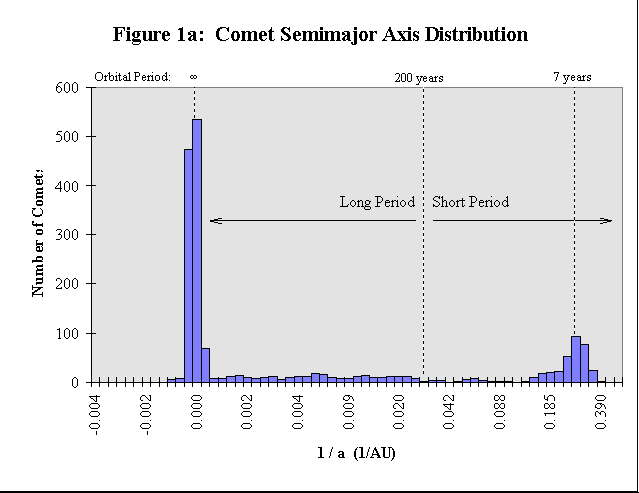
Figure 1a shows the semimajor axis distribution of comets as it is often shown; the number of comets within each incremental semimajor axis range is plotted on a semi-log graph versus the inverse of the semimajor axis, 1/a, rather that the semim ajor axis, a, itself. Comets with 1/a values close to zero have long orbital periods, whereas comets with larger 1/a values have shorter orbital periods. Those comets with negative 1/a values appear to have unbounded, hyperbo lic orbits, and those with 1/a = 0 exactly appear to have marginally unbounded, parabolic orbits.2 Comets with 1/a £ 0 have been observed rather poorly and have equally poorly determined orbits; these c omets most likely have highly elliptical, nearly parabolic orbits with 1/a ³» 0.2 The semimajor axis distribution of comets appears to be divided into two populations: those that have very small 1/a val ues, and those that have 1/a values more evenly distributed up to 1/a » 1.
Figure 1b shows the orbital eccentricity distribution of comets plotted throughout its allowable range. Comets that have orbital eccentricities, e, close to zero have nearly circular orbits, whereas comets with higher eccentricities have ellip tical (or even nearly-parabolic or hyperbolic) orbits. Here again, the orbital inclination distribution of comets appears to be divided into two populations: those that have very low i, and those with i more evenly distributed from 0 to 1.< /P>
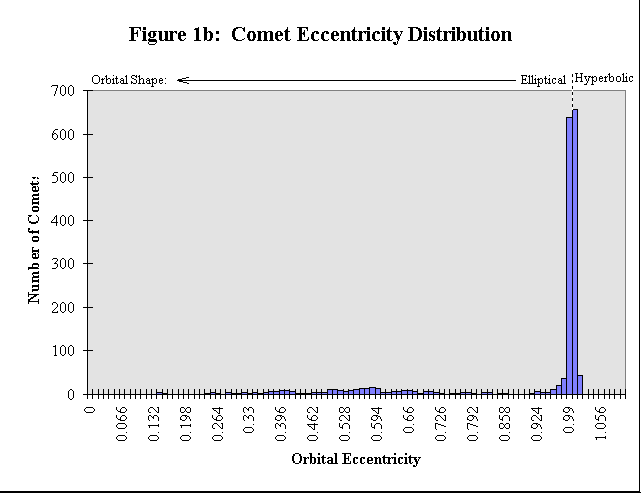
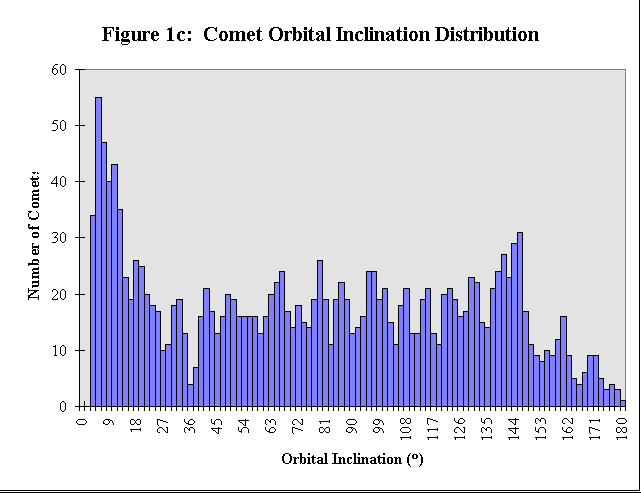
Figure 1c shows the orbital inclination distribution of comets plotted throughout its allowable range. Comets that have orbital inclinations, i, close to zero orbit close to the orbital plane of, and in the same direction as, the major bodies i n the solar system, whereas comets with higher inclinations orbit in all directions about the Sun. Yet again, the orbital inclination distribution of comets appears to be divided into two populations: those that have very low i, and those with i more evenly distributed from 0° to 180°.
The nature of the bimodality of the semimajor axis, orbital eccentricity, and orbital inclination distributions of comets becomes apparent when the orbital elements of comets belonging to the short or long, a, i, or e groups are co mpared with one another. It has been found that those comets with short a are also those which have small e and small i, and those comets with long a are also those which have larger e and larger i. Some example s of individual comets and their orbital elements are given in Table 1. No such bimodality appears in the distributions of the remaining spatial orbital elements; this lack of bimodality would be expected from the azimuthal symmetry of the solar system. The orbital element distributions of comets for the remaining orbital elements: the longitude of the ascending node, W, and the argument of perihelion, w, are plotted in Figures 1d and 1e, respectivel y.
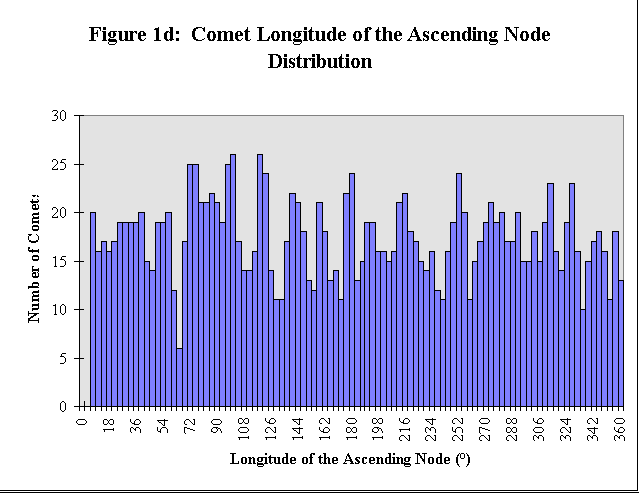
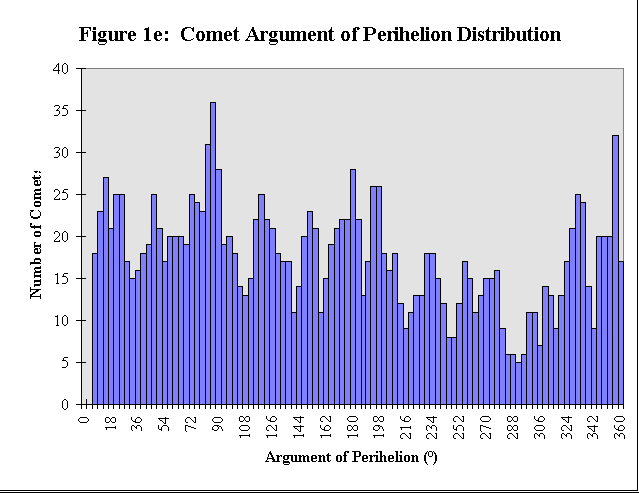
Table 1: Comet Orbital Elements
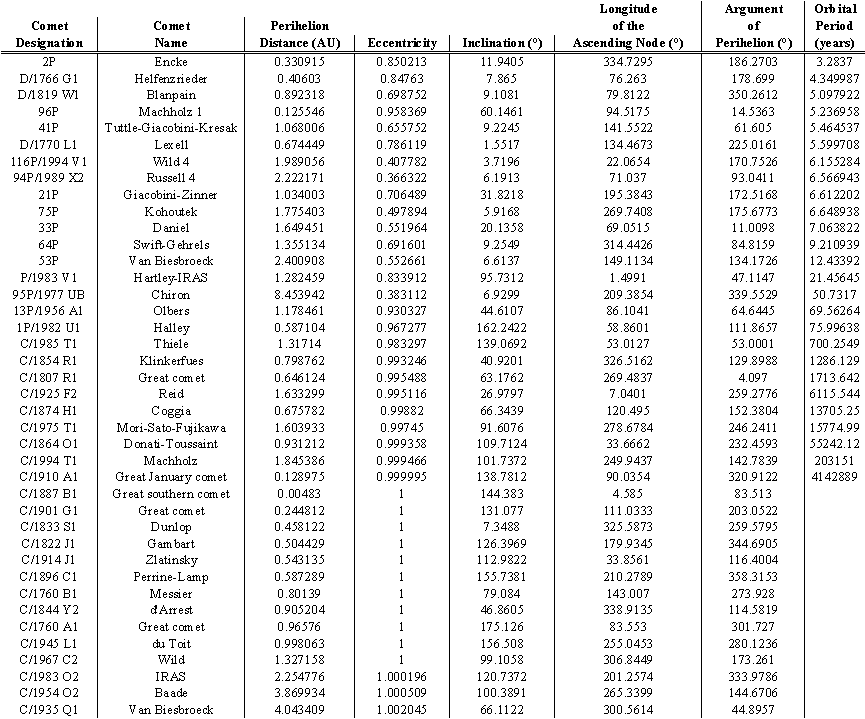
The bimodal distribution in the semimajor axes, orbital eccentricities, and orbital inclinations of comets is evidence for two separate populations of comets.2 One population consists of those with short a, small e, and small i. These short-a comets necessarily have short orbital periods as well. Members of the short-a, small-e, small-i comet population are therefore referred to as short-period comets. The other, long a, larger e , and larger i population of comets necessarily have long orbital periods. Members of the long-a, larger-e, larger-i comet population are referred to as long-period comets. A somewhat arbitrary division point of P = 200 y ears has been chosen with which to classify comets; those comets with P < 200 years are referred to as short-period comets, whereas those comets with P ³ 200 years are referred to as long-period comets.2
The division of comets into two distinct populations can be understood as a consequence of the origin hypothesis of comets and the solar system as a whole. The solar system is believed3 to have originated from a large cloud of gas and dust in interstellar space. Triggered by some as-yet-unknown event, this cloud of mostly hydrogen and some helium gas began to collapse under the influence of its own gravity. This collapsing cloud had a small, random amount of angular momentum which prevent ed it from collapsing uniformly but instead allowed it to collapse more along its axis of rotation than perpendicular to its axis of rotation. This form of collapse produced a thin rotating disk of gas and dust with a much larger concentration of matter at the center of the disk. The central, high-density portion of the disk collapsed and ignited to form the Sun. Immediately surrounding the infant Sun, smaller concentrations of gas and dust collapsed and swept up matter surrounding them to form the pla nets, moons, and asteroids. Matter in the outermost, colder portions of the disk condensed into a multitude of cometary bodies.
The hypothesized disk of cometary bodies left over from the original condensation of the solar system is named the Kuiper belt, after Gerard Kuiper who first postulated its existence in 1951.4 The Kuiper belt is believed to extend from outs ide the orbit of Neptune to 100 AU or more outwards from the Sun (see Figure 2).
Occasional interactions of the Kuiper belt objects with the outer planets Neptune, Uranus, Saturn, and Jupiter, are believed5 to have ejected a relatively small proportion of the Kuiper belt objects into highly eccentric orbits. These eject ions would occur randomly in all directions, and would boost the semimajor axes of the ejected objects to very large values. The ejected bodies are believed5 to have formed a spherical cloud of cometary bodies extending to tens of thousands of AU outwards from the Sun (see Figure 2). The hypothesized spherical cloud of cometary bodies is named the Oort cloud, after Jan Oort who first postulated its existence.5
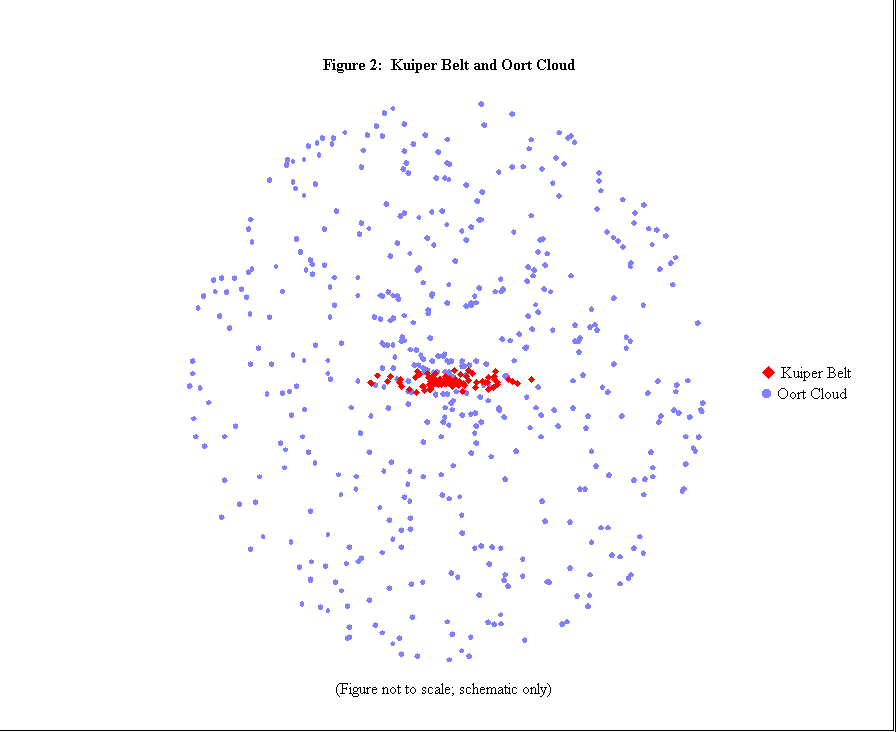
The existence of the Oort cloud was first hypothesized by Oort in 19505 based upon an analysis of 1/a values, as updated here in Figure 1a. Oort postulated that the spherical cloud of comets (which would bear his name) was the immedi ate source of all long-period comets. The large semimajor axes, random inclinations, and random arguments of perihelion of the long-period comets strongly indicate an origin in a large spheroidal cloud, many thousands of AU across.
Similar arguments based upon the orbital element distribution of comets were made by Kuiper5 to postulate the existence of the Kuiper belt. The Kuiper belt is believed to be the immediate source of all short-period comets. The relatively s mall semimajor axes and orbital inclinations of short-period comets strongly indicate an origin in a thin disk just beyond the orbit of Neptune.
The existence of the Kuiper belt was simply a hypothesis constructed to explain the origins of comets until a series of discoveries began in 1977 when an object was discovered by Kowal6 orbiting the Sun beyond the orbit of Saturn. The objec t orbited well beyond where any asteroid should be, in an orbit somewhat similar to that of a comet, but it didn't appear to be a comet. The object, temporarily named 1977 UB, was considered to be an unusual minor planet;7 it was eventually gi ven the official designation (2060) and the name Chiron. This large, dark-red object would remain a lone anomaly until a second object, 1992 AD, was discovered 15 years later. 1992 AD, soon designated (5145) and named Pholus, also orbited in a way simil ar to a comet where no asteroids were to be found, and it didn't appear to be cometary. Pholus' orbit carried it from just within Saturn's orbit to just beyond Neptune's orbit. A new category of objects in the solar system had been found: the Centaurs. Since the discovery of Pholus, four more Centaurs have been discovered (see Table 2).8 The Centaurs are believed9 to be large comet progenitors which have been perturbed by other objects and injected into the in ner solar system from the Kuiper belt. The hypothesis that the Centaurs are cometary bodies has been partially confirmed by the recent discovery of gaseous CO emissions (a uniquely cometary trait) from Chiron as it approaches perihelion.10 Si nce this discovery, (2060) Chiron has been given the additional designation of Comet 95P/Chiron.10
Table 2: Kuiper Belt Candidate Objects
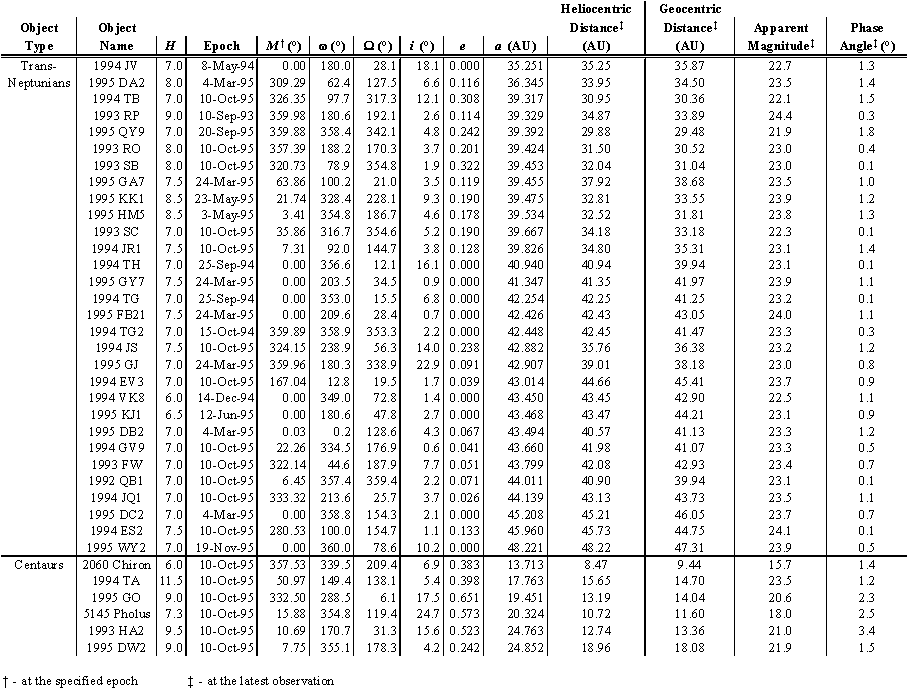
The first object actually residing in the Kuiper belt was discovered in 1992. Object 1992 QB1 was found to orbit more than 40 AU from the Sun, more than 1.3 times as far from the Sun as Neptune. Five more trans-neptunian objects were discovered in 19 93; twelve more were discovered in 1994; and twelve trans-neptunians have been discovered so far in 1995. A total of 30 trans-neptunian, Kuiper belt candidate objects with at least approximate orbits have been discovered so far (see Table 2) .8 The Hubble Space Telescope was recently used in an attempt to detect some of the fainter members of the Kuiper belt.11 In a series of images covering a small region of the sky, the Hubble detected 29 trans-neptunian objec ts. Although these objects were found to be orbiting well beyond Neptune, the images were not sufficient to calculate orbits for the objects or to warrant assigning them designations. An illustration of the orbits of the outer planets, the Centaurs, and the TNOs is shown in Figure 3.
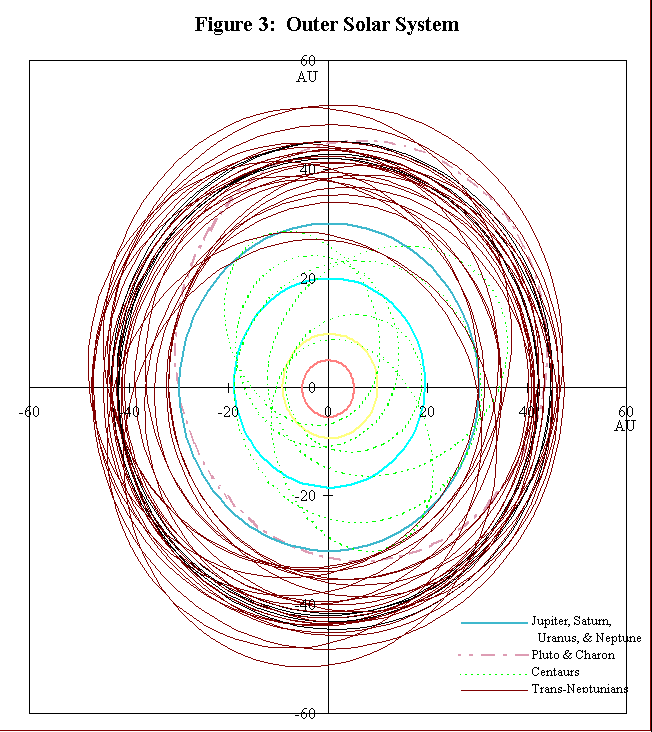
Observational evidence, including the TNOs and Centaurs which have been discovered, tends to support the existence of the Kuiper belt. The hypothesis that the observed trans-neptunian objects are indeed the first few members of the Kuiper belt to be o bserved is examined in this study. Evidence to test this hypothesis has been obtained by comparing the observed magnitude distribution of the TNOs with the observed magnitude distribution of short-period comets.
Procedure & Results
I expect that the magnitude distributions of populations of objects will be similar if the populations are related to one another. For this reason, I have calculated magnitude, size, and mass distributions for the trans-neptunian objects and magni tude distributions for the short-period and long-period comets. Comparisons between the magnitude distributions of these populations have provided some insight into the relationships among these objects. I have derived extrapolations of these distributi ons based upon the magnitude and size distributions. The theoretical magnitude and mass distributions were derived from the theoretical size distribution as described below.
The size distribution of any particular population of solar system bodies of one particular type should be of the form:
[Eqn. 1]
where: c>(r) is the cumulative number of objects with radius ³ r, c>0 is a positive real constant, and s is a positive real constant.
This distribution should form a straight line of negative slope when plotted on a log-log graph. The theoretical size distribution c>(r) can be fitted to the observed size distribution data to provide an extrapolation into size regimes that are underrepresented or totally absent in the observational data. Care must be taken to fit the ideal distribution curve to those portions of the data sets which are not significantly underrepresented. In choosing a fit to the distributions throughout this study, I have used the least-squares fit to those data points, in the well-represented portion, which result in the highest correlation coefficient.
Size measurements must be obtained for the population of objects under consideration before their size distribution can be calculated. Size measurements are not available for the trans-neptunian objects (TNOs) or for most comets, h owever. Size estimates must therefore be made based upon the objects' brightness’ and distances from the Sun and the Earth. Albedo values must be assumed for the TNOs in order to estimate their sizes.
I have established the relationship between the magnitude and radius of an object by making several assumptions. The objects under consideration have been assumed to be spherical with a constant (average) albedo over their surfaces. The intensity of light reflected to the observer has been assumed to fall off as the square of both the Sun-to-object and object-to-Earth distances. I have derived the resulting magnitude-radius relationship to be:
[Eqn. 2]
where: r is the object radius, R is the Sun-to-object distance, D is the object-to-Earth distance, a is the albedo, f is the fractional projected illuminated area that is visible from Earth, m1 is the apparent magnitude, and g is a positive constant for the entire solar system.
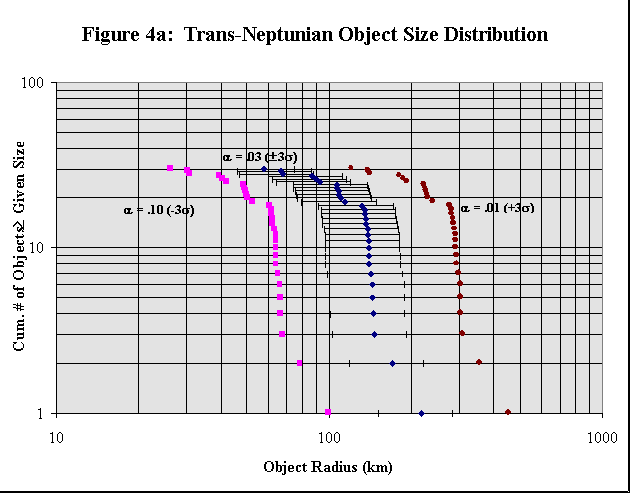
I have determined g for the solar system by averaging the values obtained for g for each of several solar system bodies. The solar system bodies used and each of their g values are given in Table 3. The average value of g (which was used hereinafter in this analysis) was found to be g = 656 km/AU2. The standard deviation for this value of g is s = 40.5 km/AU2. Three standard deviations were added to or subtracted from the nominal value of g as well as using the minimum or maximum albedos to obtain estimates for the minimum and maximum sizes of objects. The TNO size distributions for each of the minimum, nominal, and maximum albedo values: 0.01, 0.03, and 0.10, respectively, are shown in Figure 4a. These albedo values were chosen to reflect the observed albedos of Chiron, Pholus, Pluto, Charon, and Triton.
Table 3:
g Values of Solar System Bodies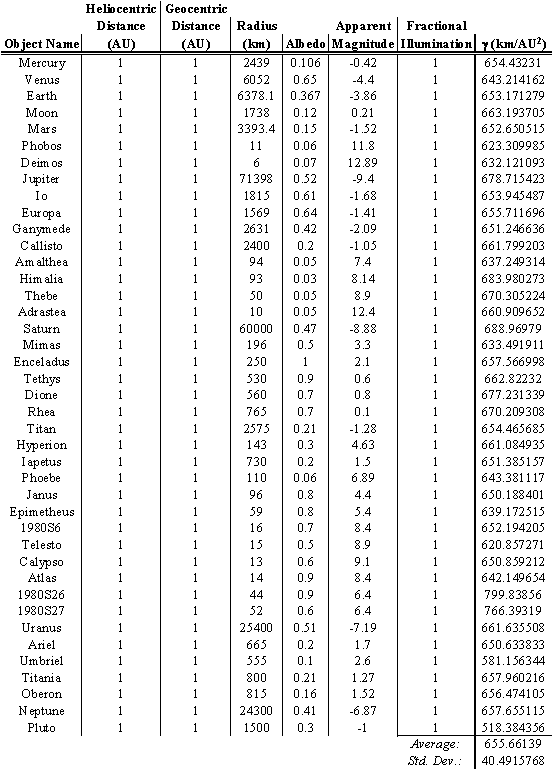
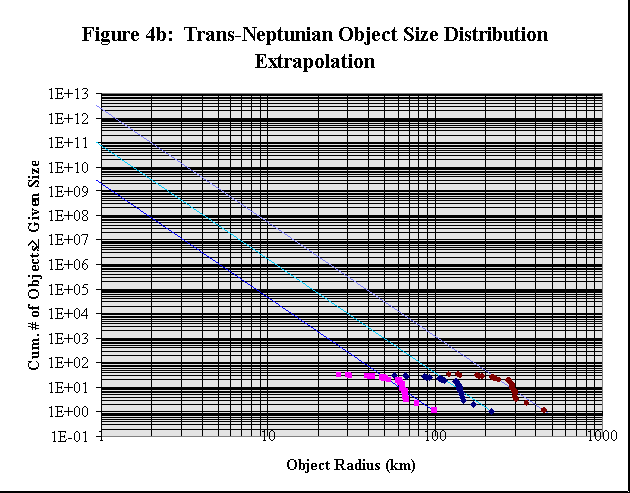
Extrapolations of the TNO size distribution to sizes not represented in the observed population may be made by extending the fitted curve described by Equation 1. Extrapolations to smaller sizes in particular can be used to estimate the total number o f TNOs that may be present. The extrapolated size distributions for the albedo values previously used are shown in Figure 4b.
Extrapolations based upon the TNOs which have been observed would only indicate the number of TNOs within the distance range that has been observed; TNOs which may be more distant from the Sun and the Earth may not be detected. Extrapolations based up on the observed TNOs alone may therefore misrepresent the population of TNOs in the hypothesized Kuiper belt. This misrepresentation may be corrected by calculating and similarly extrapolating the magnitude distribution of the TNO population.
I have derived the expected magnitude distribution of a population of objects, which conform to the size distribution described by Equation 1 and whose magnitude-radius relationship is described by Equation 2, as outlined in Appendix A. The population of objects is assumed to be uniformly distributed (the number of objects of a given size per unit volume is constant) throughout a (negligibly) thin disk which extends from an inner radius of Ri to an outer radius of Ro. The point of view of the observer is also assumed to be sufficiently close to the Sun so that D » R. The derived magnitude distribution of such a population of objects is given as:
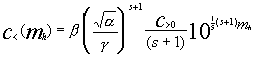[Eqn. 3]
where: c<(mh) is the cumulative number of objects with "heliocentric" magnitude £ mh (the "heliocentric" magnitude, m< SUB>h, is the apparent magnitude which would be observed from the viewpoint at the Sun), b is a positive constant parameter which is based upon the size of the disk, and the other parameters are as defined previously.
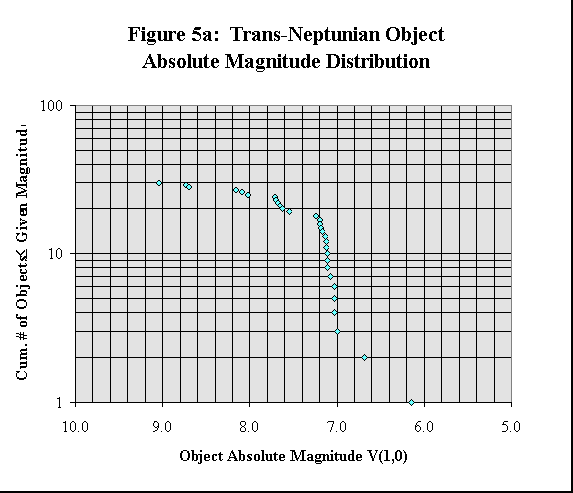
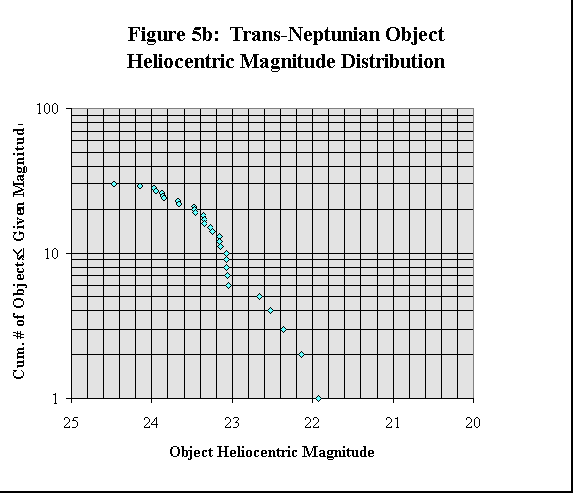
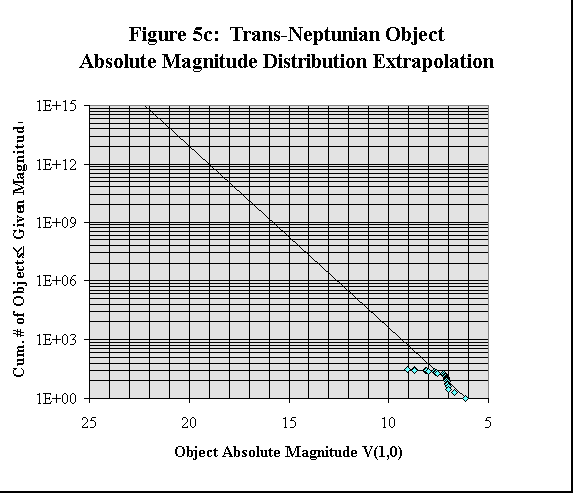
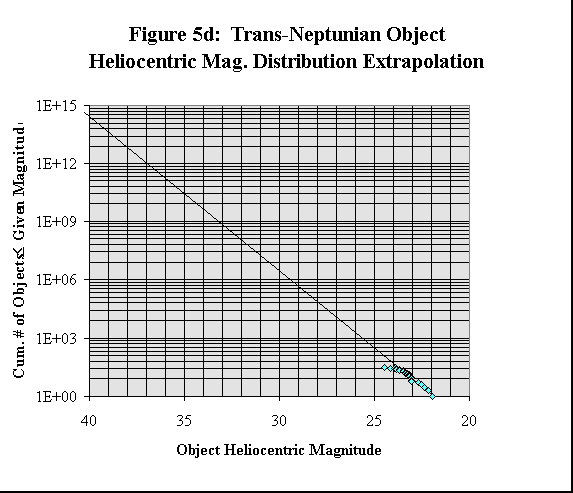
< /DIR>The magnitude distribution described by Equation 3, including appropriate values for a, Ri, and Ro, has been fitted to the observed magnitude distribution of the TNOs to obtain corrected va lues of c>0 and s. The observed and extrapolated TNO absolute magnitude and heliocentric magnitude distributions are shown in Figures 5a, b, c, and d.
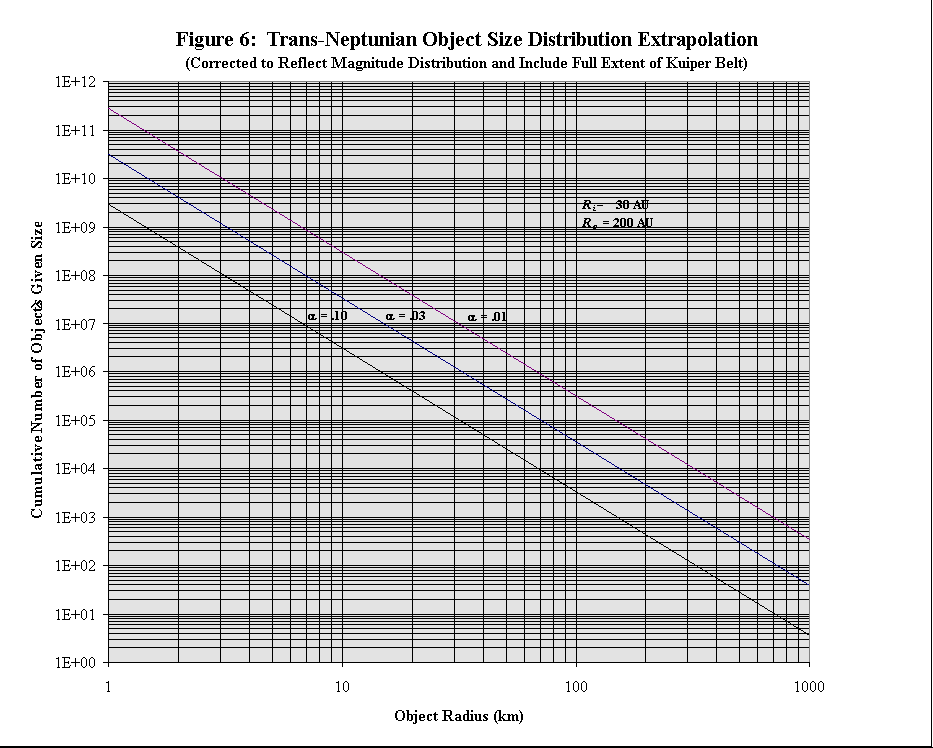
The corrected values of c>0 and s have been used in Equation 1 to recalculate the extrapolated size distribution of TNOs so as to reflect the contribution from unseen TNOs throughout the hypothetical Kuiper belt and to corre ctly reflect the magnitude distribution. The corrected value of s obtained from the observed heliocentric magnitude distribution is s = 2.97; for Ri = 30 AU and Ro = 200 AU, the corrected values of c >0 obtained from the observed heliocentric magnitude distribution are c>0 = 2.87´109, 3.13´1010, 2.77´1011, for a = 0.10, 0.03, 0.01, respectively. Extrapolations of the corrected size distribution of TNOs have been used to reestimate the cumulative number of trans-neptunian objects larger than a given size. The corrected extrap olations of the TNO size distribution is shown in Figure 6.
Estimates of the mass distribution of TNOs have also been made based upon the corrected size distribution of TNOs. The expected mass distribution of objects with the properties previously assumed and the size distribution described by Equation 1 has b een derived as described in Appendix B. The mass density distribution of individual objects of any size throughout the disk, r(r,R), is assumed to be a constant, r, a nd the value of the parameter s is assumed to be less than 3 (a slightly different equation would be obtained for other values of s). The derived mass distribution of such a population of objects is given as:
[Eqn. 4]
where: M<(r) is the cumulative mass of all objects with radius £ r, r is a the (constant) mass density of each object, and the other paramet ers are as defined previously.
The derived mass distribution of the TNOs is shown in Figure 7.
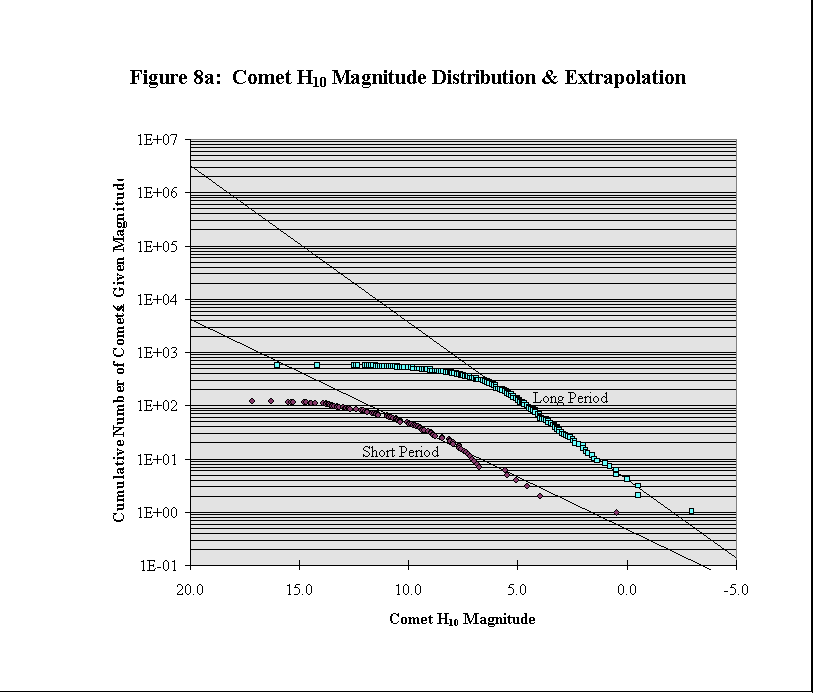
The magnitude distributions of short-period comets should follow the same distribution as described by Equation 3, but with different values for the parameters c>0, s, and b, as should all other di stinct populations of solar system objects, with the H10 magnitudes of comets being used instead of (and equivalent to) their absolute magnitudes. The H10 magnitudes of many comets have been obtained from the Houston Comet Catalo gue.12 The H10 magnitude distributions of short-period and long-period comets and fitted extrapolations to the distributions is shown in Figure 8a.
Discussion
The (uncorrected) trans-neptunian object (TNO) size distribution shown in Figure 4a displays some interesting features. In the well-represented, larger-radius portion, the distribution contains two distinct (log-log) linear portions, perhaps indic ating two distinct populations of objects. The three largest objects seem to fall along one population line, and the third- through the eighteenth-largest objects fall very well along another population line. I believe that the true population line for the TNOs (if there is indeed only one) probably lies somewhere in-between the two population lines apparent in the TNO size data because the larger-radius population line is due to only three data points; not very much upon which to make a case for multip le TNO populations.
The underrepresented portion of the TNO size distribution, where the distribution deviates from an ideal population distribution, contains a step-like effect in which small groups of data points seem to follow their own (log-log) linear population line s, with discontinuities between each of these data point groups. This step-effect could be due to the low precision of the TNO apparent magnitudes from which their sizes are estimated; quantization of the apparent magnitude data would lead to quantizatio n in the estimated sizes. I believe that when more accurate measurements of the TNOs are available, and when more individual TNOs have been observed, this quantization effect should vanish.
The fitted extrapolations of the TNO size data, as shown in Figure 4b, provide an estimate for the total number of TNOs which may exist. Assuming the TNOs are relatively highly reflective (a = .10) and using three standard d eviations of error in my g estimate gives at least a billion (109) TNOs that have radii of at least 1 km. Assuming the TNOs are poorly reflective (a = .01) and again using three standard de viations of error in my g estimate gives up to a trillion (1012) or more TNOs that have radii of at least 1 km. These estimates, while generally indicative of the great number of Kuiper belt members (far outnumbering any other population of objects in the Solar System), are not very precise and only give an order of magnitude estimate of the number of bodies populating the Kuiper belt and the Solar System.
The TNO magnitude distribution, as shown in Figure 5, is somewhat better behaved than the TNO size distribution. The TNO heliocentric magnitude distribution (see Figures 5b and 5d) fits an extrapolated population line fairly well. The only anomaly th at is apparent is a series of four or five TNOs which all have roughly the same heliocentric magnitudes (23.0 to 23.1) instead of gradually getting brighter. It seems as if a portion of the population line were 'broken' off from the rest and 'bent' downw ards towards dimmer magnitudes. The adjustment in heliocentric magnitude which would be necessary to 'straighten-out' the TNO heliocentric magnitude distribution is well within the typical observational errors associated with the TNOs. Such a correction adjustment may occur when more precise measurements of the TNOs have been made.
The TNO absolute magnitude distribution is shown in Figure 5a. Although the TNO absolute magnitude distribution is not expected to follow the magnitude distribution described by Equation 3, it is expected to follow a similar, (semilog) linear distribu tion. An extrapolation of the TNO absolute magnitude distribution is therefore shown in Figure 5c as well. The TNO absolute magnitude distribution shows the same features as the TNO size distribution in Figure 4a, as would be expected.
The TNO size distribution extrapolation, corrected to reflect the observed TNO heliocentric magnitude distribution and to include the full extent of the Kuiper belt, is shown in Figure 6. This size distribution is based upon an assumed Kuiper disk ext ending uniformly from an inner radius, Ri, of 30 AU to an outer radius, Ro, of 200 AU. Adjusting the inner or outer boundaries of this hypothesized Kuiper disk would not affect the slope of the population distribution lines, but would only shift the population lines to greater or lesser cumulative numbers of objects. For these values of Ri and Ro (this value of Ro is rather speculative), the estimated number of obj ects at least 1 km in radius is very close to that obtained from the uncorrected size distribution in Figure 4b; there are many billions (109) of TNOs at least 1 km in radius.
One notable difference between the corrected and uncorrected size distribution extrapolations is apparent; the corrected size distribution extrapolation predicts substantially more TNOs of greater sizes. The corrected size distribution extrapolation i ndicates that several Pluto-sized objects (perhaps hundreds) exist throughout the Kuiper belt. This extrapolation bolsters the idea that Pluto and Charon are really trans-neptunian, Kuiper belt objects that were captured into their present, Neptune-reson ant orbit by indicating that there should be many other similar-sized objects as well; if so, one would expect a few of them to be occasionally captured into Neptune-resonant orbits, or by Neptune itself.
The TNO mass distribution extrapolation is shown in Figure 7. This TNO mass distribution is based upon the same Kuiper disk used to generate the corrected size distribution extrapolation in Figure 6, with the constant mass density of individual TNOs e qual to 0.5 g/cm3. I chose this particular density to be the same as the most likely density of comet Shoemaker-Levy 9 as determined by Asphaug13 because short-period comets are believed to originate in the Kuiper belt, as described earlier. The TNO mass distribution extrapolation is remarkably flat; the slope of the TNO mass distribution is sufficiently close to 1 that, within the error of measurement, it could be greater than 1 or identically equal to 1. This corresponds to the value of s used in Equations 1, 3, and 4 being greater than or equal to 3, contrary to the assumption s = 3 used to derive Equation 4 in Appendix B. The alternate versions of Equation 4 which would result for s ³ 3 are similar enough to that resulting from s < 3 so as to not significantly change the cumulative mass distribution within the Kuiper belt. As for the total mass present in the Kuiper belt, the calculated TNO mass distribution extrapola tion indicates that there is approximately "a large terrestrial planet's worth" of mass (~1025 kg) in the Kuiper belt.
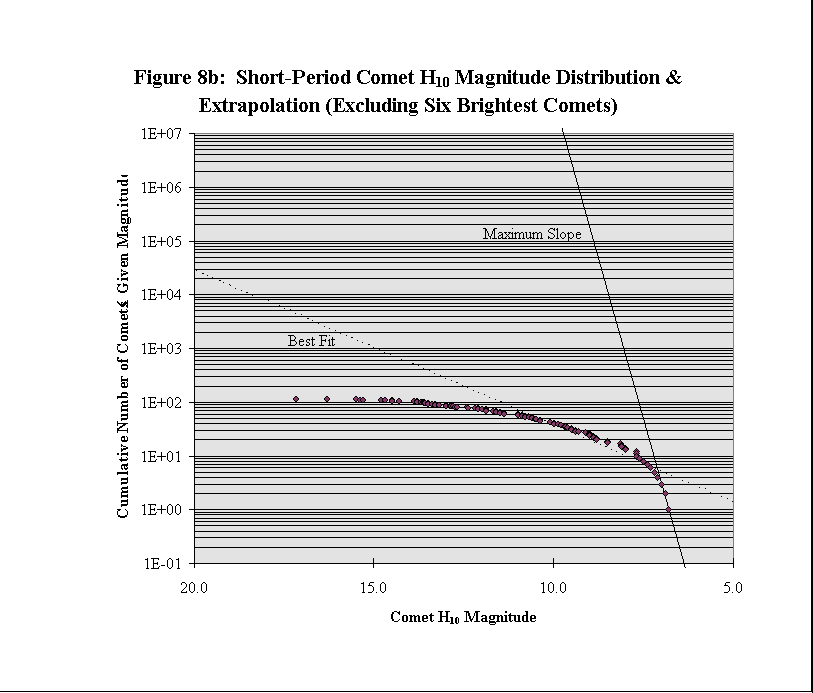
The H10 magnitude distributions of short-period and long-period comets for which H10 magnitudes have been calculated is shown in Figure 8a along with the extrapolated fits to their data. The long-period comets fit very well to an ideal population distribution line, with a sharp drop-off corresponding to the underrepresented and relatively underobserved data portion. The short-period comets however, do not fit to any particular population distribution line very well. There is a nearly (semilog) linear data portion within the main body of the data, shown along the solid population line in Figure 8b. This population line is far different from the population line obtained by fitting to the entire (supposedly) well-represented port ion of the short-period comet data. The population line fitted to the entire well-represented data portion is shown as the dotted line in Figure 8b. The six brightest short-period comets: P/Schwassmann-Wachmann 1, P/Olbers, P/Pons-Brooks, P/Halley, P/Sw ift-Tuttle, and P/Holmes, at H10 magnitudes: 5.6, 5.5, 5.1, 4.6, 4.0, and 0.5, respectively, are much brighter than, and don’t follow the magnitude distribution trend of, the other short-period comets. Aside from the actual values of their per iods, these six comets fit very well into the long-period comet population; I suspect that they actually belong in the long-period comet distribution. Perhaps these six comets are not part of the same population of comets which are thought to originate i n the Kuiper belt, the short-period comets, but instead have been misclassified because of their orbital periods and they actually belong to the population of comets which are thought to originate in the Oort cloud, the long-period comets. Further analys is of the orbital elements and possible evolutionary history of certain short-period comets may indicate that some short-period comets evolved into their present orbits from long-period, Oort cloud-originating, orbits; I suspect that such short-period com ets may have once been long-period comets.
The best-fit population lines for the trans-neptunian objects, long-period comets (LPCs), short-period comets (SPCs), the best-fit population line and maximum slope population line for the short-period comets (without the six brightest comets), and the (base-10 semilog) slopes of these lines are shown in Figure 9.
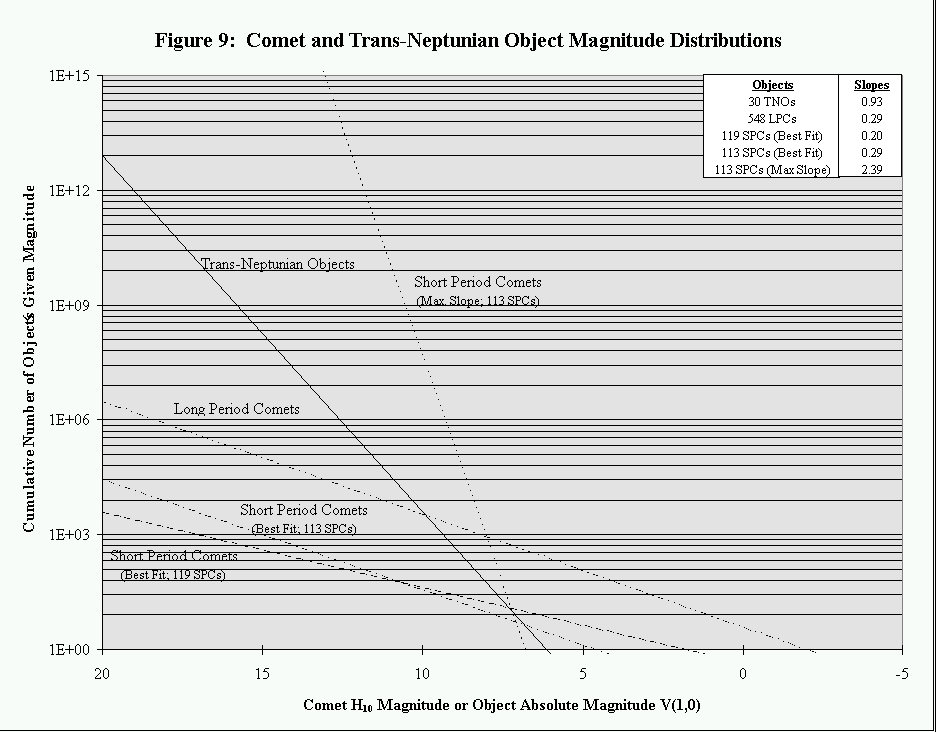
The slope of the population line for the long-period comets is nearly identical to that of the short-period comets with the six brightest SPCs removed from the SPC population and added to the LPC population. This not only supports the generally accept ed idea that the SPCs and LPCs are related, but also supports the idea that those six brightest SPCs discussed previously are indeed misclassified as part of the Kuiper belt (short-period) population of comets instead of the Oort cloud (long-period) popul ation of comets.
I expected that the slope of the cumulative population distribution line of the TNOs would be similar to that of the short-period comets, thereby supporting the hypothesized relationship between TNOs, the Kuiper belt, and short-period comets. The popu lation lines for these groups of objects are significantly different however. The SPCs do not seem to have any clearly-defined population line (hence the three different population lines given), which makes it difficult to compare with the TNO population line. The TNO population line does not fall along a slope near to any of the three possible SPC population lines. Although many more H10 magnitude measurements of many more short-period comets could refine the SPC population line to be close r to that observed for the TNOs, I interpret the population difference as follows: while the observed trans-neptunian objects are likely to be the first of many in the Kuiper belt, the trans-neptunian objects that have been observed may not be representat ive of the Kuiper belt as a whole. I expect that the trans-neptunian object population distribution will more closely approach that of the short-period comets once many more TNOs farther out in the Kuiper belt have been observed. I expect that the TNO p opulation distribution is shallower than what we have observed as yet; the small portion of the Kuiper belt that we have observed is more heavily populated than the main, outer portion of the Kuiper belt.
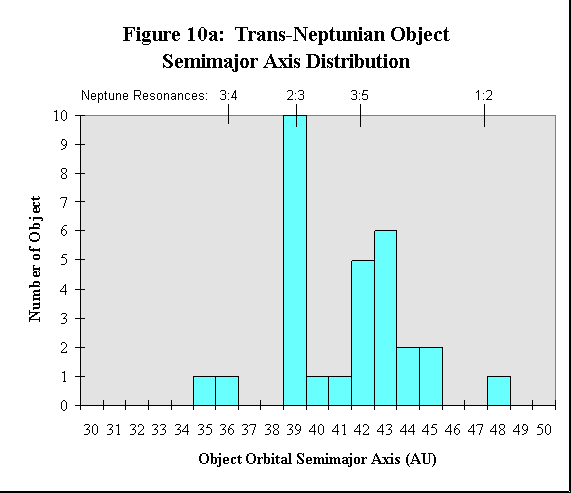
I have determined the TNO incremental semimajor axis distribution, as shown in Figure 10a, to help support this hypothesis. The TNOs are strongly clustered around those semimajor axes which have resonant orbits with Neptune’s orbit. In fact, a third of the TNOs are clustered around the 2:3-resonance at 39.45 AU, as is the Pluto-Charon pair. This clustering at the 2:3-resonance in turn supports the notion that Pluto and Charon are Kuiper belt/trans-neptunian objects that were captured into resonance with Neptune. I expect that more TNOs will be found clustered around, or totally absent from, the strongest Neptune-resonant orbits. Outside of these resonant orbits, I expect the TNO population distribution the better reflect the short-period comet dis tribution.
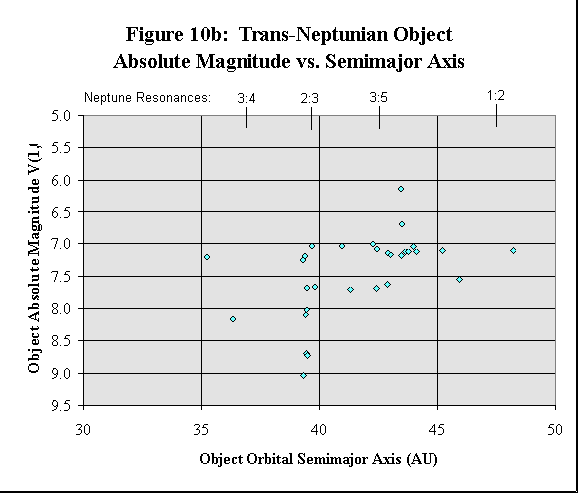
I have also plotted the TNO absolute magnitudes vs. their semimajor axes in Figure 10b to support the proposed segregation and/or clustering of TNOs. Not only is the resonant clustering apparent in Figure 10b, but the observed TNOs appear to be mostly in the 7.0 to 7.7 magnitude range, with the exception of eight TNOs of brighter or dimmer magnitudes clustered around the Neptune-resonant orbits. Five dimmer TNOs are clustered around the 2:3-resonance, two brighter TNOs are just beyond the 3:5-resonan ce, and one dimmer TNO seems out-of-place at the 3:4-resonance.
Conclusions
As a result of this study, I conclude the following:
References
1 Orbital element data for comets obtained from: B. G. Marsden & G. V. Williams, Catalogue of Cometary Orbits 1995, Minor Planet Center, Smithsonian Astrophysical Observatory , Cambridge (1995)
2 L. Kresak, "Discoveries, Statistics, Observational Selection," L. L. Wilkening, ed., Comets, Arizona (1982), pp. 56-82
3 M. L. Kutner, Astronomy: A Physical Perspective, Wiley, New York (1987), pp. 507-512
4 R. Cowen, "Frozen Relics of the Early Solar System," Science News, vol. 137, pp. 248-250 (1990)
5 P. R. Weissmann, "Comets at the Solar System’s Edge," Sky & Telescope, pp. 26-29 (January 1993)
6 G. Hahn & M. E. Bailey, "The Changing Face of Chiron," Astronomy, pp. 45-48 (August 1990)
7 A. Stern, "Chiron: Interloper from the Kuiper Disk?," Astronomy, pp. 28-33 (August 1994)
8 Orbital and observational data for Centaurs and Trans-Neptunian objects obtained from: Minor Planet Center Computer Service, Minor Planet Circulars, and Minor Planet Electronic Circulars, Smithsonian Astrophysical Observatory, Cambridge (19 95)
9 W. A. Arnett, Internet URL: http://seds.lpl.arizona.edu/nineplanets/nineplanets/kboc.html, Lunar and Planetary Laboratory, University of Arizona (1995)
10 B. G. Marsden & G. V. Williams, International Astronomical Union Circular Number 6193 (28 July 1995)
11 R. A. Kerr, "Home of Planetary Wanderers is Sized Up for the First Time," Science, vol. 268, p. 1704 (23 June 1995)
12 J. R. Bollinger & C. A. Wood, Houston Comet Catalogue, Lunar and Planetary Institute, Houston (1984)
13 E. Asphaug & W. Benz, "Density of Comet Shoemaker-Levy 9 deduced by modelling breakup of the parent ‘rubble pile’," Nature, vol. 370, pp. 120-124 (14 July 1994)
Appendix A
Derivation of Cumulative Magnitude Distribution c<(mh)
Given a number density (number of objects of a particular radius, r, at a particular distance from the Sun, R, per unit volume): n(r,R) º n(r); (i.e. - independent of R)
the total number of objects, n(r),of a given radius, r, throughout a thin disk of inner radius Ri and outer radius Ro is: 
and given a cumulative size distribution (cumulative number of objects greater than radius r): 
; where 
, and c>0 and s are positive
constants;
then: 
Integrating this expression gives the following:
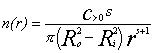and 
Assuming the radius-magnitude relation: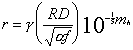 
,
the expression for n(r) can be rewritten as the number density of objects of a particular apparent magnitude, m1, at a particular distance from the Sun, R, per unit volume:
Appendix A
(continued)
Assuming that D » R, f º 1 (
), and 
the total number of objects, n(mh),of a given heliocentric magnitude, mh, throughout a (negligibly) thin disk of inner radius Ri and outer radius Ro is: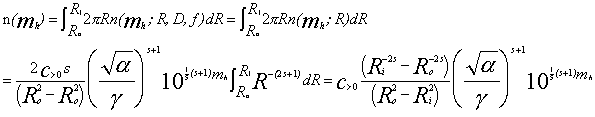 
The cumulative heliocentric magnitude distribution (cumulative number of objects with heliocentric magnitude less than mh) is: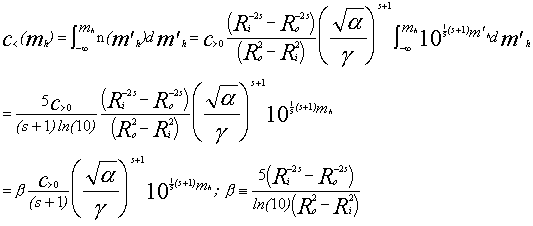 
Appendix B
Derivation of Cumulative Mass Distribution M<(r)
Given a number density (as derived in Appendix A), n(r), of spherical objects of uniform individual mass density, r, distributed uniformly throughout a thin disk, the disk mass d
ensity, m(r), of objects of a given radius, r, is: 
and the disk cumulative mass distribution, M<(r), is: 
Recalling (from Appendix A) that 
and 
, then similarly, 
where e is an arbitra
rily small constant.
Integrating by parts to get M<(r) gives: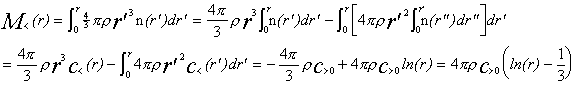 
for s º 3, and 
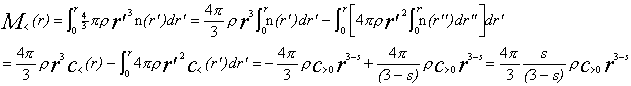for s ¹ 3.
Appendix B
(continued)
For s º 3 then, the cumulative mass, M(r1, r2), of objects with radii greater than r1 and radii less than r2 is:
; 
for 0 < s < 3, the cumulative mass, M<(r), of objects with radii less than r is: 
and similarly, for s > 3, the cumulative mass, M>(r), of objects with radii greater than r is: 
Go Back to the list of Alex Willman's Recent Work
Go Back to Alex Willman's Home Page
