Reaction Engineering of Polymer Electrolyte Membrane Fuel Cells
A new approach to elucidate the operation and control of Polymer Electrolyte Membrane (PEM) fuel cells is being developed. A global reactor engineering approach is applied to PEM fuel cells to identify the essential physics that govern the dynamics in PEM fuel cells. Reaction engineering principles are employed to develop a one-dimensional differential PEM fuel cell suitable for elucidating the dynamic performance of PEM cells under well-defined conditions.
Polymer Electrolyte Fuel Cells
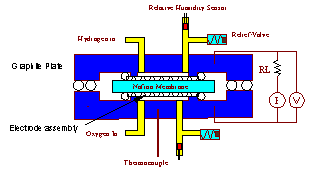
Polymer electrolyte membrane (PEM) fuel cells employ a polymer membrane with acid side groups to conduct protons from the anode to cathode. Water management in the fuel cell is critical for PEM fuel cell operation. Sufficient water must be absorbed into the membrane to ionize the acid groups; excess water can flood the cathode of the fuel cell diminishing fuel cell performance limiting the power output. A schematic of a polymer electrolyte membrane hydrogen-oxygen fuel cell is shown in Figure 1.
|
|
Figure 1. Hydrogen-oxygen PEM fuel cell. Hydrogen molecules dissociatively adsorb at the anode and are oxidized to protons. Electrons travel through an external load resistance. Protons diffuse through the PEM under an electrochemical gradient to the cathode. Oxygen molecules adsorb at the cathode, are reduced and react with the protons to produce water. The product water is absorbed into the PEM, or evaporates into the gas streams at the anode and cathode. |
Proton conductivity in Nafion, and most other polymer electrolytes, increases with water activity, and is maximized when equilibrated with liquid water (water activity aw=1). Operation at aw=1 minimizes the membrane resistance for proton conduction, but results in water condensation which inhibits mass transfer to the electrodes. Our research is focused on finding optimal operational and control schemes for water management in PEM fuel cells.
The Fuel Cell as a Chemical Reactor
The dynamic response of fuel cells is essential for transportation applications where the power demand will need to respond to variable loads.
We have developed a one-dimensional differential reactor that functions as a Stirred Tank Reactor PEM fuel cell to study fuel cell dynamics. The STR PEM fuel cell is one-dimensional and the gas compositions at the anode and cathode can be independently controlled and measured. The dynamic response of the STR PEM fuel cell is much easier to analyze and interpret than for a conventional PEM fuel cell. The performance of larger complex fuel cell reactor systems may be modeled based on collections of the STR PEM fuel cell.
Our initial fuel cell studies have with three fundamental questions.
- Is there an optimum membrane water content that will provide high conductivity while avoiding flooding in the electrodes?
- Water is produced by the fuel cell reaction; how should the feed streams and their water content be controlled to respond to load variations?
- How should the fuel cell be started up from different initial conditions to achieve the desired power output?
The STR PEM fuel cell is shown schematically in Figure 2. The reactants are fed to gas plenums where the residence time is greater than the characteristic diffusion time in the plenum, so the gas phase compositions are uniform, and the only gradients are transverse to the membrane. This is a one-dimensional reactor, and both the anode and cathode may be considered as stirred tank reactors (STR PEM fuel cell).
|
|
|
|||
|
Figure 2A. Schematic of the STR PEM fuel cell reactor. The exposed membrane area was ~1.5 cm2, with gas volumes above the anode and cathode of ~0.2 cm3. The MEA employed Etek electrodes and a Nafion 115 membrane. |
Figure 2B. Photograph of the STR PEM fuel cell reactor. The graphite plates were fitted into Teflon plates and sandwiched between Al blocks with were heated. Relative humidity sensors measured the temperature and RH in the effluent streams. |
Ignition in Autohumidification PEM fuel cells
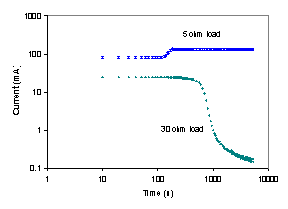
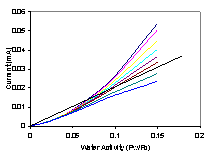
The startup and steady state operation of the autohumidification PEM fuel cell was examined. Figure 3 shows the current of the autohumidification PEM fuel cell during startup. The results show classic ignition phenomena. At 50ºC with an external load resistance of 5 Ω and initial water loadings of <1.7 H2O/SO3 the fuel cell approaches an extinguished state, where the steady state current is very low (~0.1 mA). When the initial water loading is >1.8 H2O/SO3 the fuel cell “ignites” and approaches a “high current” steady state current of ~ 125 mA(Moxley, Tulyani et al. 2003). Increasing the load resistance can limit the current and result in the fuel cell current being extinguished (see Figure 3B).
|
|
|
|
Figure 3A. Start-up of an autohumidification PEM fuel cell with different initial membrane water loading (l=water molecules per SO3). The fuel cell was run at 50ºC after initial membrane humidification at 25ºC for varying periods of time. The external resistance was 5 W. |
Figure 3B. Start-up of a PEM fuel cell humidified to an initial water content of l~2 at 50°C. The upper curve was obtained with an external load resistance of 5 W; the lower curve was obtained with an external load resistance of 30 W. |
Ignition/extinction is indicative of multiple steady states in PEM fuel cell operation (the same reactor conditions, feed flow rates, temperature and load resistance can result in two different stable operating states). Steady state multiplicity in the autohumidification PEM fuel cell results from a positive feedback between water production and the membrane resistance. The fuel cell reaction to make water is limited by the proton conductivity of the polymer electrolyte. The water produced by reaction decreases the membrane resistance. The lower resistance permits a greater proton current, which leads to more water production. The feedback loop for ignition by water in the STR PEM fuel cell is completely analogous to the classic thermal ignition phenomenon.(Moxley, Tulyani et al. 2003)
The membrane resistance for proton conduction decreases exponentially with water activity in the membrane, aw; the experimental data for Nafion 115 is fit very well with the expression, Rm=107*exp(-14(aw)0.2) W-cm. (Yang, Benziger, et al. J. Membrane Science 2004)
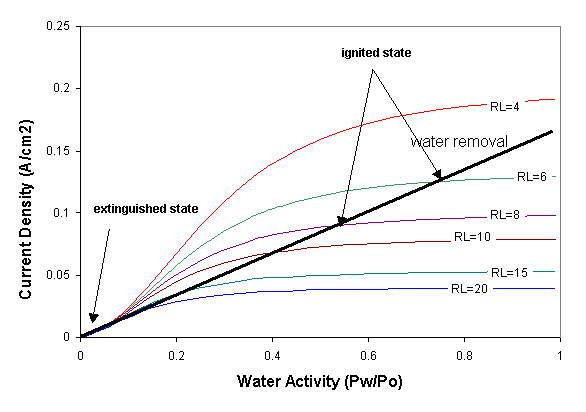
Water removal and water production are balanced at steady state. Water production and removal can be expressed as functions of the water activity and steady state can be represented by the intersections of water production and removal curves. Water removal is by convection and scales linearly with the water activity in the membrane. Water production increases sigmoidally with membrane water activity due to the decrease in resistance. Water production also increases with decreasing external load resistance. The steady states are identified in Figure 4.
|
Unstable state
|
|
Figure 4. Water production and removal rates for the STR PEM fuel cell. The water production curves are the sigmoidal curves. The water removal line is based on the assumption of equilibrium water activity between the membrane and the gas phases at the anode and cathode. The low water activity region is blown up in the insert at the upper left. Increasing the temperature of the fuel cell has little effect on the sigmoidal water production curves but increases the slope of the water removal line. |
Fixing the load resistance and cell temperature results in either a one or three intersections of the water production and water removal curves corresponding to steady states. At a high load resistance and high temperature there is a single low current or “extinguished” steady state. At moderate load resistances and low temperature there are three steady states. In addition to the extinguished state, there is a high current or “ignited” steady state, and there is an intermediate steady state.
Where three steady states exist only two are stable. Both the ignited and extinguished steady states are stable to fluctuations away from the steady state. For example, a positive fluctuation from the ignited state increases the water content in the membrane, at that condition the water removal is greater than the water generated so the system will return to steady state. The middle steady state is unstable, positive fluctuations in the water content from that steady state will cause the system to generate more water than is removed and the fuel cell will evolve towards the ignited steady state; negative fluctuations in water content from the intermediate state will drive the system towards the extinguished state. The critical water content shown in Figure 3 corresponds to the water content of the unstable steady state in Figure 4. According to Figure 4 the critical water activity for ignition is ~ 0.1, which corresponds to a water loading l~1.7 H2O /SO3.
More Steady States
Based on the results above it was expected that increasing the cell temperature and increasing the load resistance would increase the rate of water removal and decrease the water production, which should extinguish the fuel cell current. Much to our surprise the behavior was not that simple.
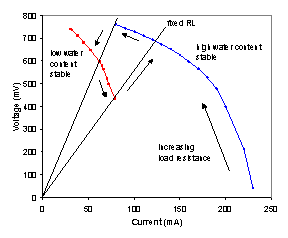
Figure 5A shows the steady state polarization curve for the autohumidification PEM fuel cell at 95ºC. This data was taken by changing the load resistance and allowing 2-4 hours for the cell current to come to steady state (the polarization curve took 4 days to obtain!). The current and voltage changed smoothly until the load resistance was increased from 11 to 12 Ω, at which point the steady state current and voltage both decreased abruptly. The resistance was increased stepwise from 12 to 20 Ω and the current and voltage changed smoothly. Starting with a load resistance of 20 Ω the process was reversed. The current and voltage changed smoothly along the same curve as for the increasing resistance, but there was no abrupt change in the current and voltage at 11 Ω. Instead the IV data varied smoothly until the resistance was decreased below 5 Ω, when it jumped up. The polarization curves in Figure 5A show a hysteresis loop, where the steady state current and voltage depend on the direction of approach. The experiments identified 3 stable steady states (which imply a total of 5 steady states). We refer to the three stable steady states by the relative water content in the membrane as inferred from the membrane resistance. The three states are the dry state (extinguished current), low water content state (intermediate current) and high water content state (highest current branch).
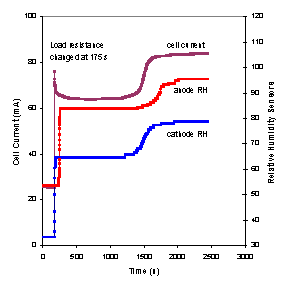
The dynamics of the transitions between the high and low water content states shown in Figure 5A are unusual. Shown in Figures 5B is the current responses to step changes in the resistance which jump across the hysteresis loop shown in Figure 5A. The response to changes in resistance produce a rapid response followed by a long delay and then a second change in the current to the new steady state.
|
|
|
|
Figure 5A. Polarization curves for autohumidification PEM fuel cell at 95ºC with H2 flow and O2 flow of 10 mL/min. The high water content curve was taken after establishing steady state with a load resistance of 2 Ω. The low water content curve was taken after establishing steady state with a load resistance of 20 Ω. |
Figure 5B. Fuel cell current at 95ºC and relative humidity in the anode and cathode effluents in response to a step decrease in the external load resistance from 25 W to 5 W. The switch was made at 175 s. |
The dynamic responses shown in Figures 5B and 6C show an instantaneous change where the current follows the load. This change corresponds to a condition where the water content in the membrane remains is fixed. There is a longer response that corresponds to the fuel cell membrane adjusting the water content to a new steady state value. The dynamics of transitions between steady states shown took 103 – 104 s for a new steady state to be achieved after changing the external load resistance.
The reason for the slow dynamics of PEM fuel cells is because the membrane acts as a reservoir for water. The water content of the membrane must equilibrate with the water production and water removal rates from the fuel cell. The characteristic time for water produced to be taken up by the membrane is ~ 100 seconds.
Mechanical Properties of Membranes and Fuel Cell Operation
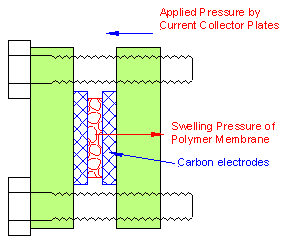
The five steady states were only observed above a minimum temperature. We advance the conjecture that the three stable steady states and the stepwise decrease in the membrane resistance result from a coupling of mechanical and chemical effects. The polymer membrane in the MEA is pressed between the graphite plates (with the gas flow channels) and the porous carbon electrodes, spatially confining the membrane. As the membrane takes up water, the proton conductivity increases, but the membrane must also swell. However, being spatially confined, the membrane is not free to swell; it must do work to push the electrodes apart, or to swell into the porous electrode. Water uptake is hindered by these spatial constraints, just like the absorption of water by a sponge is restricted when the sponge is confined between two plates. The energy required for swelling (or shrinking) of the membrane depends on the material properties of the membrane. Increasing temperature and increasing water content both reduce the elastic modulus of the Nafion membrane. Additionally, the glass transition temperature of Nafion decreases with water content, which dramatically alters the elastic modulus. Above a critical temperature and membrane water content, the swelling pressure of the membrane is reduced to the point where it is not sufficient to push the electrodes apart and absorb more water.
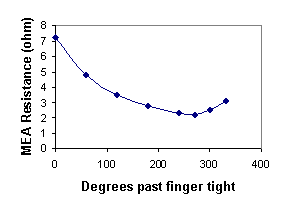
The effect of the spatially confined MEA on the water uptake is to “pin” the membrane water content at fixed values until the membrane swelling pressure becomes sufficient to overcome the applied force of the electrodes. By pinning the water content, the proton conductivity is also effectively pinned. The MEA resistance as a function of the sealing on the MEA is plotted in Figure 6B. The initial decrease in the MEA resistance results from improving the membrane-electrode contact reducing the interfacial resistance. The MEA resistance goes through a minimum and then increases as the bolts are tightened further. We attribute the eventual increase in MEA resistance with increased compression to water being squeezed out of the membrane.
|
|
|
|
Figure 6A. Schematic of the sealing of the MEA in the STR PEM fuel cell. |
Figure 6B. Effective MEA resistance as a function of sealing pressure on the MEA. The bolts on the plates sealing the MEA were tightened past figure tight and the MEA resistance was determined from the minimum slope of the polarization curve in the ohmic region. |
OSCILLATIONS
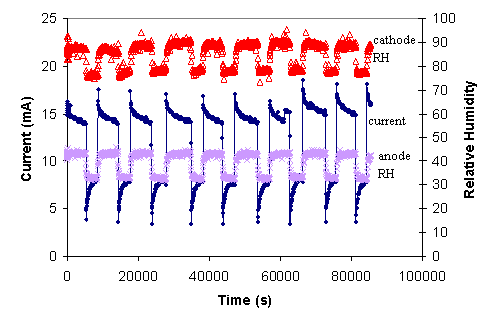
After the STR PEM fuel cell had been operated continuously for over 5000 hours the fuel cell started displaying autonomous oscillations. For temperatures between 50-100ºC with external load resistances varying from 0.2-20 W the system would settle into a state with autonomous oscillations after 24 hours. Current, voltage and relative humidity of the anode and cathode effluents were monitored over a broad range of conditions, and autonomous oscillations persisted for 7000 hours. (The STR PEM fuel cell operated continuously for 12,000 hr.) During the time period between 5000-12,000 hr of operation the oscillations had a very regular characteristic shape as shown in Figure 7.
|
|
|
Figure 7. Characteristic autonomous oscillations observed with the STR PEM fuel cell during 5000-12,000 hours of operation. These are stationary states. The feeds were dry with flow rates 10 mL/min H2, 10 mL/min O2. The cell temperature is 80ºC, with a load resistance of 10 W. |
The current and voltage show regular relaxation oscillations, resembling the opening and closing of a capacitive switch. The oscillations abruptly rise then decay to a high current plateau; after a period of several thousand seconds the current or voltage precipitously drops, and then rises to approach a low current or voltage. The relative humidity of the anode and cathode effluents tracks the rise and fall of the current oscillations. The cathode effluent relative humidity rises coincident with the current increase. There is a time delay of ~100 s from the current increase until the relative humidity at the anode starts rising.
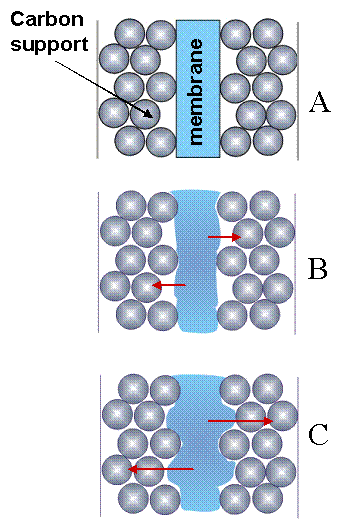
Why are the transitions between states so abrupt? We suspect that membrane swelling and relaxation processes create an interfacial contact switch between the membrane and the electrode. We propose a very simple model for this process. The electrode is composed on micron sized carbon particles, on which Pt nanoparticles are supported. The particles are fused together with binder material and coated onto a woven cloth. The membrane has a smooth surface and contacts the outermost layer of catalyst particles, as suggested in Figure 8(A). As the membrane absorbs water it swells, extruding in the gap between the carbon particles. After it swells sufficiently, it contacts the second layer of catalyst particles, as suggested in Figure 8(C). When contact is made with the second layer of catalyst particles, the interfacial resistance drops by almost a factor of two and the current jumps up. The capacitive double layer of protons that builds up on the catalyst particles is discharged when contact is made. The swollen membrane is stressed; the corrugation of the membrane surface is a high energy state. Stress relaxation of the polymer causes the extruded dimples touching the second layer of catalyst to slowly relax and stretch out in the plane of the membrane. When it breaks contact with the second layer of catalyst particle, the current drops and the water content in the membrane starts to decrease. Some of the protons are drawn off to replenish the double layer, conceivably causing the current undershoot.
|
|
|
Figure 8. Membrane swelling and the interfacial contact of the electrode and membrane. (A) The membrane initially contacts the top layer of carbon particles. (B) As the membrane takes up water it swells and pushes into the gaps of the catalyst particles, (C) eventually touching the second layer of catalyst particles. |