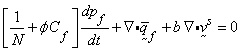9.2.0.7 Coupled Thermo-Solid Equation
QDC_THERMAL
Element_name = QDC_Thermal , etc…
< stress material data >
< heat conduction material data >
< body force data>
< connectivity data >
< field output data >
For thermal applications, NED =
(NSD+1) degrees of freedom are assigned to each node. The first NSD degrees of
freedoms are solid kinematic degrees of freedom, in the 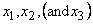 directions, and the
last degree of freedom is assigned to the temperature.
directions, and the
last degree of freedom is assigned to the temperature.
In the parabolic mode (diffusion analysis), the element is used for
solution of the following coupled equations:

where
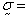 solid stress,
solid stress, 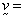 solid velocity,
solid velocity, 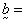 body force
body force 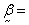 thermal moduli,
thermal moduli, 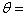 temperature, T0
= reference temperature,
temperature, T0
= reference temperature, 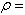 mass density,
mass density, 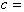 specific heat,
specific heat, 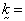 thermal conductivity,
thermal conductivity, 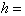 heat source.
heat source.
In the hyperbolic mode (dynamic analysis), the element is used for
solution of the following coupled equations:

where
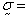 solid stress,
solid stress, 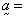 solid acceleration,
solid acceleration, 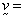 solid velocity,
solid velocity, 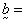 body force,
body force, 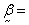 thermal moduli,
thermal moduli, 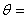 temperature, T0
= reference temperature,
temperature, T0
= reference temperature, 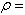 mass density,
mass density, 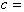 specific heat,
specific heat, 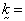 thermal conductivity,
thermal conductivity, 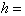 heat source.
heat source.
References / Bibliography
1. Prevost, J.H., and Tao, D.J., "Finite
Element Analysis of Dynamic Coupled Thermoelastic Problems with Relaxation
Times," J. Appl. Mech., ASME,
Vol. 50, (1983), pp. 817-822.
2. Tao, D.J., and Prevost, J.H.,
"Relaxation Effects on Generalized Thermoelastic Waves," J. Thermal Stresses, Vol. 7, (1984), pp.
79-89.
3. Tao, D.J., "Finite Element Analysis
of Thermoelasticity Problems,"
Ph.D. Thesis, Department of Civil Engineering, Princeton University,
Princeton, New Jersey, (June 1984).
9.2.0.8 Heat Equation
QDC_HEAT
Element_name = QDC_Heat ,
etc…
< heat conduction material data >
< body force data>
< connectivity data >
The element is used for solution of
the following scalar heat equation:
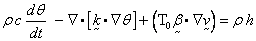
where
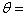 temperature,
temperature, 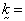 thermal conductivity,
thermal conductivity, 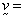 solid velocity,
solid velocity, 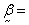 thermal moduli, T0
= reference temperature,
thermal moduli, T0
= reference temperature, 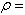 mass density,
mass density, 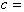 specific heat,
specific heat, 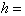 heat source. For heat
diffusion (parabolic mode) and heat conduction (elliptic mode) one degree of
freedom is assigned to each node for the temperature.
heat source. For heat
diffusion (parabolic mode) and heat conduction (elliptic mode) one degree of
freedom is assigned to each node for the temperature.
9.2.0.9 Heat Transport Equation
HEAT_TRANSPORT
Element_name = HEAT_TRANSPORT, etc…
< material data >
<body force data >
< connectivity data >
The element is used for the solution
of the following scalar equation:
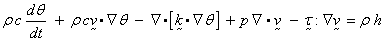
where
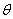 = temperature;
= temperature; 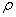 = mass density; c
= specific heat;
= mass density; c
= specific heat; 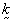 = diffusion/dispersion
coefficient;
= diffusion/dispersion
coefficient; 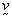 = flow velocity; p =
fluid pressure;
= flow velocity; p =
fluid pressure; 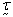 = fluid viscous
stress; and h = heat source. One
degree of freedom is assigned to each node for the temperature.
= fluid viscous
stress; and h = heat source. One
degree of freedom is assigned to each node for the temperature.
9.2.0.10 Electric Charge Equation
QDC_CHARGE
Element_name = QDC_charge, etc...
< charge conduction material model >
< body force data >
< connectivity data >
The element is used for solution of
the following electric charge equation:
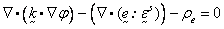
where
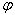 = electric potential,
= electric potential, 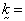 permittivity matrix,
permittivity matrix, 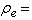 electric volume charge
density,
electric volume charge
density, 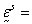 solid strain, and
solid strain, and 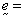 piezoelectric constants
(third-order tensor, viz.,
piezoelectric constants
(third-order tensor, viz., 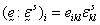 ). For this element,
one degree of freedom is assigned to each node for the electric potential.
). For this element,
one degree of freedom is assigned to each node for the electric potential.
9.2.0.11 Coupled
Porous Solid – Pore Fluid Equations
9.2.0.11.1 Diffusive equations:
QDC_POROUS_2
Element_name = QDC_Porous_2 , etc…
< stress material data >
< scalar diffusion material data >
< body force data >
< connectivity data >
< field output data >
In the parabolic mode (diffusion
analysis) the element is used for solution of the following coupled equations:

where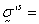 solid (effective) stress,
solid (effective) stress, 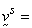 solid velocity,
solid velocity, 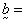 body force (per unit
mass),
body force (per unit
mass), 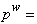 pore fluid pressure,
pore fluid pressure, 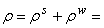 total mass density,
total mass density, 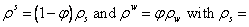 solid mass density,
solid mass density, 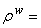 fluid mass density and
fluid mass density and
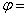 porosity;
porosity; 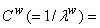 fluid compressibility,
fluid compressibility, 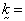 hydraulic conductivity
[L/T], and
hydraulic conductivity
[L/T], and 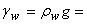 fluid unit weight,
fluid unit weight, 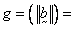 acceleration of
gravity. In that case, NSD solid
kinematic degrees of freedom are assigned to each node, in the
acceleration of
gravity. In that case, NSD solid
kinematic degrees of freedom are assigned to each node, in the 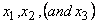 directions,
respectively, and the degree of freedom (NSD+1) is assigned to the pore fluid
pressure.
directions,
respectively, and the degree of freedom (NSD+1) is assigned to the pore fluid
pressure.
9.2.0.11.2 Dynamical equations:
QDC_POROUS_1
Element_name = QDC_Porous_1 , etc…
< stress material data >
< scalar diffusion material data >
< body force data >
< connectivity data >
< field output data >
In the hyperbolic mode (dynamic analysis) the element is used for solution
of the following coupled equations:

where
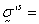 solid (effective) stress,
solid (effective) stress, 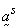 = solid acceleration,
= solid acceleration, 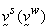 solid (fluid) velocity,
solid (fluid) velocity, 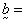 body force (per unit mass),
body force (per unit mass), 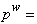 pore fluid
pressure
pore fluid
pressure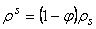 and
and 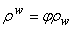 with
with 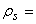 solid mass density,
solid mass density, 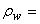 fluid mass density and
fluid mass density and
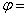 porosity;
porosity; 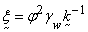 with
with 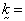 hydraulic conductivity
[L/T] and
hydraulic conductivity
[L/T] and 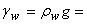 fluid unit weight,
fluid unit weight, 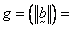 acceleration of
gravity. In that case, NSD solid
kinematic degrees of freedom are assigned to each node, in the
acceleration of
gravity. In that case, NSD solid
kinematic degrees of freedom are assigned to each node, in the 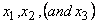 directions,
respectively, and the degrees of freedom (NSD+1), (NSD+2), etc… are assigned to
the fluid motion in the
directions,
respectively, and the degrees of freedom (NSD+1), (NSD+2), etc… are assigned to
the fluid motion in the 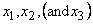 directions,
respectively.
directions,
respectively.
In the case of a compressible pore fluid, the pore fluid
pressure is determined from the computed velocities through time integration of
the following equation:
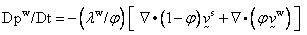
where
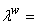 fluid bulk
modulus. In the case of an incompressible pore fluid, the pore
fluid pressure is determined from the computed velocities through the following
equation:
fluid bulk
modulus. In the case of an incompressible pore fluid, the pore
fluid pressure is determined from the computed velocities through the following
equation:
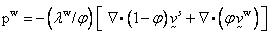
where
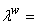 a penalty parameter.
a penalty parameter.
References / Bibliography
1. Prevost, J. H.,"Mechanics of
Continuous Porous Media," Int. J.
Eng. Sci., Vol. 18, No. 5, (1980), pp.787-800.
2. Prevost, J.H., et al.,"Offshore
Gravity Structures: Analysis," J.
Geotech. Eng.
Div., ASCE, Vol. 107, No. GT2, (1981), pp. 143-165.
3. Prevost, J.H.,"Nonlinear Transient
Phenomena in Saturated Porous Media," Comp.
Meth. Appl. Mech. Eng., Vol. 30, No. 1, (1982), pp. 3-18.4.
4. Prevost, J.H.,"Implicit-Explicit
Schemes for Nonlinear Consolidation," Comp.
Meth. Appl. Mech. Eng., Vol. 39, (1983), pp. 225-239.
5. Prevost, J.H.,"Nonlinear Transient
Phenomena in Soil Media," Chapt. 26 in Mechanics
of Engineering Materials, Eds C.S. Desai and R.H. Gallagher, Wiley, (1984),
pp. 515-533.
6.
Prevost, J.H.,"Wave Propagation in Fluid-Saturated
Porous Media: an Efficient Finite Element Procedure," Int. J. Soil Dyn. Earthq. Eng., Vol. 4, No. 4, (1985),
pp. 183-202.
9.2.0.12 Darcy
Flow Equation
Darcy’s law for the flow of viscous
fluid in a permeable medium, and conservation of mass are written as follows:
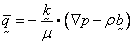 (1)
(1)
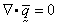 (2)
(2)
where 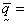 Darcy velocity; p = fluid pressure,
Darcy velocity; p = fluid pressure, 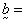 body force (per unit mass),
body force (per unit mass), 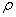 = fluid mass density,
= fluid mass density, 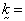 intrinsic permeability with units [L2] (see Section 10.16), and
intrinsic permeability with units [L2] (see Section 10.16), and 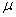 = fluid viscosity.
= fluid viscosity.
Two
formulations of the Darcy flow equation are available: (1) a primal formulation
which amounts to solving a Poisson problem for the pressure; and (2) a mixed
formulation for which both the pressure and velocity are treated as unknowns.
9.2.0.12.1 Pressure Formulation:
The
equation is simply obtained by taking the divergence of Eq. 1, and leads to:
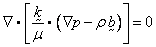
The equation is often written in terms
of the total head h as:
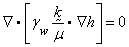
where
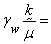 hydraulic conductivity with units [L/T];
hydraulic conductivity with units [L/T]; 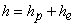 , with
, with 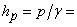 pressure head, and
pressure head, and 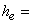 elevation head defined such that:
elevation head defined such that: 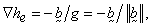 viz.,
viz., 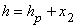 for the case
for the case 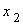 vertical and oriented positively upward.
vertical and oriented positively upward.
There is one degree of freedom assigned
to each node for the fluid pressure.
QDC_DARCY_PRESSURE
Element_name = QDC_Darcy_pressure
, etc…
< scalar diffusion material
data >
< body force data >
< connectivity data >
9.2.0.12.2 Mixed Formulation:
In the mixed formulation, both Eqs. 1
and 2 are used to compute the fluid pressure and velocity vector
components. A stabilized mixed
formulation is used. The element may be
used for both 2D and 3D applications, and equal order interpolations are used
for the fluid pressure and velocity.
There are (NSD+1) degrees of freedom assigned to each node for the
velocity vector components and the fluid pressure.
QDC_DARCY_MIXED
Element_name = QDC_Darcy_mixed
, etc…
< scalar diffusion material
data >
<
body force data >
< connectivity data >
References /
Bibliography
1. Masud, A. and T.J.R.
Hughes, “A Stabilized Mixed Finite Element Method for Darcy Flow,” Comp. Meth. Appl. Mech. Eng., Vol. 191,
(2002), pp. 4341-4370.
9.2.0.13 Pressure Diffusion Equation
The element is used for solution of the following
equations:
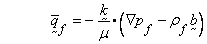 (1)
(1)
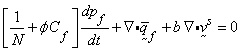 (2)
(2)
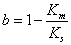
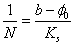
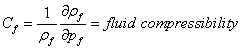
where 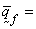 Darcy fluid velocity,
Darcy fluid velocity, 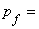 fluid pressure,
fluid pressure, 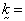 permeability (intrinsic; units [L2]),
permeability (intrinsic; units [L2]), 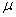 = fluid viscosity,
= fluid viscosity, 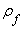 = fluid mass density,
= fluid mass density, 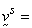 solid velocity,
solid velocity, 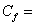 fluid
compressibility, and
fluid
compressibility, and 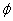 = porosity.
= porosity.
Two
formulations are available: (1) a primal formulation which solves a pressure equation,
and (2) a mixed formulation for which both the pressure and fluid motion are
treated as unknowns.
9.2.0.13.1 Pressure Formulation:
The
equation is as follows:

There is one degree of
freedom assigned to each node for the pressure.
QDCD_PRESSURE
Element_name = QDCD_PRESSURE , etc…
< scalar diffusion material data >
< body force data >
< connectivity data >
9.2.0.13.2 Mixed Formulation:
There are (NSD+1) degrees of freedom
assigned to each node for the fluid velocity and the fluid pressure.
QDCD _MIXED
Element_name = QDCD_MIXED, etc…
< scalar diffusion material data >
< body force data >
< connectivity data >
![]() directions, and the
last degree of freedom is assigned to the temperature.
directions, and the
last degree of freedom is assigned to the temperature. 
![]() solid stress,
solid stress, ![]() solid velocity,
solid velocity, ![]() body force
body force ![]() thermal moduli,
thermal moduli, ![]() temperature, T0
= reference temperature,
temperature, T0
= reference temperature, ![]() mass density,
mass density, ![]() specific heat,
specific heat, ![]() thermal conductivity,
thermal conductivity, ![]() heat source.
heat source. 
![]() solid stress,
solid stress, ![]() solid acceleration,
solid acceleration, ![]() solid velocity,
solid velocity, ![]() body force,
body force, ![]() thermal moduli,
thermal moduli, ![]() temperature, T0
= reference temperature,
temperature, T0
= reference temperature, ![]() mass density,
mass density, ![]() specific heat,
specific heat, ![]() thermal conductivity,
thermal conductivity, ![]() heat source.
heat source. ![]()
![]() temperature,
temperature, ![]() thermal conductivity,
thermal conductivity, ![]() solid velocity,
solid velocity, ![]() thermal moduli, T0
= reference temperature,
thermal moduli, T0
= reference temperature, ![]() mass density,
mass density, ![]() specific heat,
specific heat, ![]() heat source. For heat
diffusion (parabolic mode) and heat conduction (elliptic mode) one degree of
freedom is assigned to each node for the temperature.
heat source. For heat
diffusion (parabolic mode) and heat conduction (elliptic mode) one degree of
freedom is assigned to each node for the temperature.