9.16 Transmitting Nodal Boundary Element
The element is used to provide a transmitting nodal boundary for incident propagating motions, such as occur in seismic response calculation. The boundary is frequency independent, and is local in space and time (see Note at end of this chapter for more details). It is exact for vertically propagating wave motions and linear systems only. At the boundary:
where
time, 
mass density of
underlying medium, 
= wave speed, 
incident motion, 
associated
displacement motion at the node, and s = multiplier. The incident motion 
is defined by a
corresponding load-time function.
NODAL_TRANSMITTING
Element_name = NODAL_TRANSMITTING etc...
< material data >
< output requests >
< connectivity data >
9.16.1 Element Group Control Information
Must follow the element name (same data record), and define the following:
Note Variable Name Type Default Description
Number_of_material_sets integer [1] Number of material sets, Numat
File_name string [none] File name (optional). Name must be
enclosed in quotation marks.
Input_format list [*] Input format
keywords / list
9.16.2 Geometric / Material Properties Data (Numat sets)
Note Variable Name Type Default Description
• Keywords Read Method
Material_set_number integer [0] Material set number 
Numat
Incident_motion_definition list [*] Incident motion definition
displacement
velocity
acceleration
Incident_motion_load_time integer [0] Incident motion load-time function number
Motion_multiplier_i real [0.0] Motion multiplier for degree of freedom 
(
).
Rhoc_i real [0.0] 
for degree of freedom ().
• List Read Method
Geometric / material data must follow in the form:
< 
>
< 
>
< terminate with a blank record >.
EXAMPLE
Define_Element_Group /
name = "Group_3" /
element_type = nodal /
element-shape = one_node /
number_of_material_sets = 1
material_set_number = 1 /
incident_motion_definition = displacement /
incident_motion_load_time = 1 /
motion_multiplier_1 = 1.00 /
rhoc_1 = 105.175e6
NODAL_CONNECTIVITY etc…
9.16.3 Element Nodal Connectivity Data
Consult Chapter 11 for details; for this element NEN = 1.
Note/
Transmitting
Boundary
1. Introduction
The application of finite elements to the solution of problems involving the propagation of waves requires the development of special boundary conditions referred to as transmitting, non-reflecting, silent or energy-absorbing boundaries. These boundary conditions are required to use at the boundary of the necessarily finite mesh to simulate the infinite extent of the domain. For instance, when an infinite domain in the vertical direction is modeled by a finite mesh, there is danger that waves reflected from the free-surface will be reflected back off the artificial bottom boundary and cause errors in the response calculations, unless special boundary conditions can be imposed at the base of the column. In the following, a rigorous formulation of an appropriate boundary condition is presented. The proposed boundary condition is frequency independent, and is local in space and time. It is exact for linear systems only, and therefore requires that the boundary be placed at a sufficiently large distance such that the response be linear at that distance.
Seismic site response calculations are usually performed for a given seismic input prescribed in the form of an acceleration time history to be applied at the base of the soil column. As discussed hereafter, the implementation of an appropriate boundary condition at the base of the soil column requires detailed knowledge of the nature of the prescribed seismic input, viz. whether it corresponds to an incident vertically propagating motion or is the sum of an incident and a reflected motion.
The features of one-dimensional wave propagation in a semi-infinite system are first reviewed before the boundary condition is developed.
2. One-Dimensional Vertical Wave
Propagation
For the purpose of illustrating the features of the boundary formulation, the vertical propagation of shear waves is considered. The equation of motion may be expressed as:
(1)
where
a comma is used to indicate partial differentiation; mass density; 
shear modulus; 
horizontal
displacement; time; and 
depth coordinate, with
the 
-coordinate assumed oriented upwards positively. The fundamental solution of Eq. 1 can be
expressed as:
(2)
where
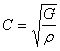(3)
and I and R are two arbitrary functions of their
arguments: 
represents a wave
motion propagating upwards in the positive -direction with the velocity C, and is referred to as the
incident motion; 
presents a wave motion
propagating downwards in the negative ‑direction with the velocity C, and is referred to as the reflected
motion. The following two identities
apply:
(4a)
(4b)
and therefore, if one differentiates Eq. 2 with respect to and 
in turn:
(5)
(6)
The shear stress
can therefore be expressed as
(7)
and upon elimination of 
the following relation
is obtained:
(8)
At this
stage it is instructive to study the total wave pattern when an incident wave
motion 
encounters an
artificial boundary at 
. Three extreme cases
can be considered as follows:
2.1 The boundary at is fixed.
Setting 
in Eq. 2 leads to:
(9)
resulting in the total wave motion:
(10)
Therefore, at a fixed boundary, the incident wave is reflected back
with the same shape but opposite sign.
2.2 The boundary at is free.
Setting 
in Eq. 7 leads to:
(11)
resulting in the total wave motion:
(12)
Therefore, at a free boundary, the incident wave is reflected back with the same shape and the same sign.
2.3 The boundary at is silent.
Selecting Eq. 4a which is identically satisfied for I as the boundary condition for 
(13)
results in 
. Eq. 13 is called the
radiation condition. It is obtained by
selecting:
(14)
When the incident wave I
encounters that boundary, it passes through it without modification and
continues propagating towards 
. No reflected wave R, which would propagate back in the
negative -direction can arise.
3. Semi-Infinite Column
Consider the situation shown in Fig.
9.13.1. An incident vertically
propagating wave I (coming from
infinity) arrives at the site, and it is sought to compute the site response
for this incident motion. The finite
element mesh has been selected to extend down to the depth 
, and an appropriate boundary condition at the base of the soil
column is sought to simulate the infinite extend of the soil domain in the
vertical downward direction. For the
purpose of illustration, it is assumed that the site consists in general, of
two homogeneous deposits with material properties as follows:
• 
above the base of the soil column: 
• 
below the base of the soil column: 
In
order to separate the influence of the incident wave from the reflected wave on
the site response, it is assumed that the incident motion disturbance spans
over a duration 
with:
and
that it reaches the location 
at time 
. Several cases are
considered as follows:
Figure 9.16.1 Semi-Infinite Layered Soil Profile
3.1 Case
1: Homogeneous semi-infinite deposit (viz., 
):
In that case the incident
vertically propagating wave arriving at at time , will reach the free surface at time 
, will be reflected back from the free surface with the same
shape and sign, and must cross the boundary at (at times 
) without any further modification and continue propagating
back towards infinity. The resulting
motions are as follows:
• at
(15)
• at
(16)
where H is the Heaviside function. this is illustrated in Fig. 9.13.1. The desired response in the finite soil column can be achieved by prescribing at the base of the soil column either the total motion or the incident part of the motion only, as follows:
> Prescribed motion (fixed base case). In that case the base input motion must be made up of the incident and reflected motions to reproduce the specified site response as
(17)
The first part of the input corresponding to 
in Eq. 17 will
propagate towards the surface and reproduce the prescribed surface motion. It will then be reflected back off the free
surface towards the fixed base where it will be reflected again with a negative
amplitude:
This reflected wave is canceled exactly by the second
part of the input motion in Eq. 17 thereby preventing any further propagation
of waves towards the surface. In other
words, the incident wave produces the surface
motion and the reflected wave cancels the reflection from the rigid base.
Remark: The total motion is the one computed in standard deconvolution procedures implemented in computer programs such as SHAKE (1972).
> Prescribed
traction (non-reflecting case). From
Eq. 8 the stress in the semi-infinite soil deposit at location can be expressed
directly in terms of the motion at the location and the incident wave
motion. Therefore, it suffices to apply
at the artificial boundary the traction:
(18)
In that case, the incident input motion is absorbed exactly at the base after reflection from the surface. Eq. 18 is the most general boundary condition since it only requires knowledge of the incident motion.
3.2 Case 2: Non-homogeneous semi-infinite
deposit.
In that case only the incident
motion is known as it arrives at location . In order to compute
the site response for this incident motion, accounting for the effects of
ensuing reflections (or no reflections if 
and 
) at the boundary , one must prescribe the input at the base of the finite soil
column in terms of prescribed tractions as:
(19)
This will ensure proper simulation of the infinite extend of the soil domain in the downward direction.
References
/ Bibliography
1. Schnabel, P.B., J. Lysmer and H.B. Seed,
"SHAKE: A Computer Program for Earthquake Response Analysis of
Horizontally Layered Sites", Report
No. EERC 72-12,
Notes . .