12.0 ANALYSIS
OPTIONS
1. The Nonlinear Semi-Discrete Finite Element Equations
The application of the finite element discretization to the governing equation(s) of a field theory generates a matrix system of equations. These equations are either zero-, first- or second-order in the time variable and are generally nonlinear. For example, nonlinear transient finite-element dynamics are characterized by the following second-order semi-discrete balance equation:
(1)
where 
= vector of
nodal accelerations; 
(t) = vector of nodal velocities, d(t) = vector of nodal displacements; M = global mass matrix; N = global vector-valued function of the displacement d
and the velocity (when e.g.
viscous effects exists); and f = f(t) = global vector representing the
applied external loads and surface tractions.
The global quantities M, N and f are assembled from the corresponding finite element matrices and
vectors. The vector N(, d) is often
denoted the "internal force."
Note that for particular constitutive models other state variables may
also influence N (for instance,
temperature in thermo-continua), but these do not need to be included in the
present discussion.
DYNAFLOW is fundamentally structured for transient analysis of nonlinear equation systems, and the solution techniques are presented in that context. Linear balance equations and eigenvalue equations are treated as special cases of the general method. In all cases, any quantities identified as "nodal variables" are to be taken as the approximate values derived from the numerical solution of the finite-element equations.
In describing a unified solution strategy for Eq. 1, it is useful to standardize the notation of the generic second-order system to read:
(2)
where a, v,
and d are vectors of nodal unknowns
with a = 
and v =. In the
presentation hereafter, the vectors d,
v, and a are referred to as the displacement, velocity and acceleration,
respectively. However, their true
physical charater is determined by the particular field theory under
consideration.
2. Time Integration
The semi-discrete finite-element equation (Eq. 2) is a system of coupled ordinary differential equations which are to be integrated in time. The system is solved by applying a step-by-step integration procedure resulting in a system of nonlinear algebraic equations. Specifically, the strategy employed is to solve the equations at discrete times tn (for n = 1, 2, 3...) for the nodal quantities d(tn), v(tn), and a(tn). The procedure starts from user-specified initial conditions:
(3)
and the initial acceleration consistent with Eq. 2 is computed as:
(4)
where M-1 denotes the inverse mass matrix. With the solution fully characterized at time t0, the objective is to compute the solution at time t1, then at time t2 and so on. Numerous algorithms are available for that purpose. DYNAFLOW uses one-step methods to carry out the time integration by assuming auxiliary relationships between the solution vectors at time steps tn and tn+1. For second-order systems, the Newmark update formulas [see Section 12.3] are used:
(5)
(6)
(7)
where 
; and dn, vn, and an are
approximations for d(t), v(t), and a(t) respectively, at time tn,
viz.,
(8)
and 
. The scalars 
and 
are algorithmic
parameters which can be chosen to ensure unconditional stability and
second-order accuracy of the time integration in the linear case.
Note that the matrix equation system
(Eq.2) can be the composite of several equation types. For example, in solid stress analysis, it
might include the equations for stress analysis and thermal analysis. In such cases, each equation type can be
assigned its own set of values for the algorithmic parameters and . However, the same time steps (t1, t2, t3,...)
apply to all equations of the system.
3. Predictor-Multicorrector Strategy
Eq. 7 is a nonlinear system of equations. The solution to this system is obtained by using an iterative strategy which is implemented by means of a predictor-multicorrector scheme applied at each time step. In this method, a series of corrected solutions are computed starting from an initial or predicted solution for the time step. Each corrected solution is used in the following iteration to compute the next corrected solution. The procedure continues until either a specified solution convergence has been obtained or a pre-specified maximum number of iterations has been executed.
The computational problem at each time
step is to determine dn+1, vn+1, and an+1,
given dn, vn, an, and 
such that Eqs. 5-7 be
satisfied. There are several ways of
implementing the recursion relationship that takes the solution from step n to
step n + 1. In DYNAFLOW the
implementation chosen is to always use the vector of nodal quantities with the
highest time derivatives as the primary unknown, viz. for the second-order
system of Eqs. 5-7 use the vector of nodal accelerations as the primary variable. Introducing a superscript to index the
nonlinear iterations, the Newmark formulas are rewritten as:
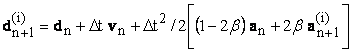(9)
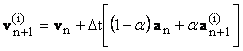(10)
Substituting
these expressions into Eq. 7 result in an equation that may be solved for 
and the
acceleration can be determined as:
(11)
where the
unknowns 
are the nodal values
of the acceleration at time tn+1. The internal force N is a system of nonlinear functionals of the solution and of the
(known) parameters an, vn, dn,
and . Once is determined,
Eqs. 9 and 10 serve to determine 
and 
.
The solution at step n + 1 is computed
by first specifying a starting value for 
, the predictor value, which corresponds to an initial guess
at the solution at time tn+1,
viz.,
(12)
except at nodes at which the motion is prescribed for which one sets:
(13)
The correctors represent the update to the nodal solution variables during each nonlinear iteration. The corrector formulas are written (from Eqs 9-11) as :
(14)
(15)
(16)
where 
= acceleration
increments which must be determined. The
correctors ensure that every set of iterates 
adhere to the Newmark
update formulas. Also note that the
correctors of the (i+1)th
iteration are computed from those of the ith-iteration
and the ith-increment of the
acceleration 
.
4. Nonlinear Iterations - Linearization
We write the resulting system of equations to be solved (Eq. 11) as:
(17)
where
(18)
and un
= {an, vn, dn} denotes the collection of known
parameters, and r = residual is a
system of nonlinear functionals of the solution an+1 and of the
parameters un and . This system is
solved for an+1 by performing a linearization via a
truncated
(19)
where the solution
increment 
is given by:
(20)
and 
are approximations of an+1
at iterations i and i + 1, respectively.
Denote
(21)
(22)
The linear system
of equations (Eq.19 ) to be solved for can be written as:
(23)
and the consistent Jacobian matrix (Eq. 22) is computed from Eqs. 17 and 18 as:
(24)
with
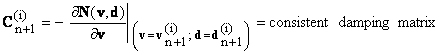(25)
and
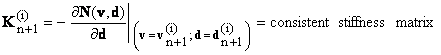(26)
The linear combination of matrices on the left-hand side of Eq. 23 is called the effective mass matrix M* where
(27)
and Eq. 23 is usually written as:
(28)
This equation is
solved for and the solution is
used in the corrector formulas (Eqs. 14-16) to compute the new iterate .
Remark: In the linear case, the assembled internal force vector N(v, d) in Eq. 2 can be represented as
N(v, d) = Cv + Kd (29)
where the damping and stiffness matrices, C and K are independent of the velocity and displacement. Then the effective mass matrix in Eq. 28 is given by:
(30)
and needs to be evaluated only when the time step value changes. The expansion in Eq. 19 is then exact, and the solution at step (n+1) is obtained as (from Eq. 28):
(31)
and (from Eqs. 14 - 16):
(32)
(33)
(34)
where the predictors 
and 
are obtained
from Eqs. 9, 10, 12 and 13.
Section 12.2 discusses the discrete time integration schemes. The various nonlinear iteration strategies available in DYNAFLOW are described in Section 12.3, and Section 12.4 describes the various linear solvers available to compute the solution to Eq. 28. In Section 12.4, the system of equations in Eq. 28 is simply viewed and solved as the linear algebraic system
Ax = b. Direct and iterative methods are provided. Section 12.5 discusses the various eigensolvers available.
Notes . .
Notes . .