12.2     Time-Integration Parameters

 

TIME_INTEGRATION

 

            TIME_INTEGRATION         integration_type =  etc...

 

Specify the parameters for the time stepping procedure to use for all equations in all subdomains/element groups belonging to any given solution stagger.

 

Note

Variable Name

Type

Default

Description

 

 

 

 

 

(1)

Integration_type

list

[*]

Implicit/explicit time integration type

 

    implicit / explicit

 

 

 

 

 

 

 

 

(2)

Equation_type

list

[*]

Equation type (see Chapter 9 for details)

 

    elliptic

 

 

   Elliptic Boundary Value problem

 

    parabolic

 

 

   Parabolic Initial Boundary Value problem

 

    hyperbolic

 

 

   Hyperbolic Initial Boundary Value problem

 

 

 

 

 

 

Analysis_type

list

[*]

Analysis type

 

    direct

 

 

   Direct one-step time integration

 

    modal

 

 

   Modal integration

 

    spectral

 

 

   Spectral integration

 

    Runge_Kutta_Cash_Karp

 

    Runge_Kutta fifth-order Cash_Karp

      integration with adaptive stepsize control

 

    Runge_Kutta_Bulirsh_Stoer

  

   Runge_Kutta integration with Bulirsh_Stoer

      steps and adaptive stepsize control

 

 

 

 

 

 

Alpha

real

[1.0]

Algorithmic parameter

 

 

 

 

   = 1.0 for Elliptic BVP

 

 

 

 

     0.0 for Parabolic Initial BVP

 

 

 

 

     0.5 for Hyperbolic Initial BVP

 

 

 

 

 

(3)

Beta

real

[0.0]

Algorithmic parameter

 

 

 

 

 

• Modal and Spectral Analysis Options

 

Number_of_modes

integer

[0]

Number of modes

 

Modal_damping_ratio

real

[0.0]

Modal damping ratio

 

 

 

 

 

• Spectral Analysis Option

 

Spectrum_load_time

integer

[0]

Spectrum load-time function number  1

 

 

 

 

 

 

EXAMPLE

            Time_integration  /

                 Integration_type  = implicit  /         # implicit time integration

                 Equation_type  = hyperbolic  /       # hyperbolic initial BVP

                 Alpha   = 0.5,     Beta   = 0.25        # Select Trapezoidal rule

 

Notes/

 (1)       Explicit time integration is performed using a diagonal mass matrix.

Notes / (cont'd)

 

(2)        The application of the finite element discretization to the governing balance equation(s) of a field theory generates a matrix system of equations.  These equations are either zero-, first- or second order in the time variable, and are referred to in the following as elliptic, parabolic and hyperbolic, respectively.  One-step algorithms are used to integrate the finite element semidiscrete equations of motion as follows (for simplicity in the presentation linear systems are used in the following):

 

A.  Hyperbolic and Parabolic-Hyperbolic Initial Boundary Value Problems: the Newmark [3] family of finite difference time stepping algorithms is used which consist of the following equations:

 

 

 

 

where  is a parameter taken to be in the interval  [1/2, 3/2] and .  Unconditional stability requires that  be taken to be in the interval .  Maximal high-frequency numerical dissipation is provided by selecting [1]  for a given .  Some well-known integrators are identified as follows:

 

Explicit central difference

  Trapezoidal

 

A particularly convenient form of C is the Rayleigh damping matrix:

 

 

where a0 and a1 are parameters (see e.g., Section 10.1) referred to as mass and stiffness damping, respectively.  Then, the resulting viscous damping can be computed as:

 

 

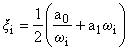
for each modal frequency i (i = 1, neq) see Fig. 12.2.1.  The parameters a0 and a1 may be selected to produce desired damping characteristics (e.g., by adjusting a0 and a1 for two eigenfrequencies).

 

 


                                                                                                overall damping

 

 

 


                   

 

 

 

 


                                                                                          damping for

                                                                                                                        damping for

 

 

 


                                                        

                                                         angular frequency                              

 

Fig. 12.2.1   Effect of Viscous Damping

 

 

As a result of the numerical integration, artificial damping and period distortion are introduced.  The following results have been obtained:

 

 

Where  = algorithmic damping ratio,  = algorithmic frequency.  Note that first-order errors resulting from  manifest themselves only in the form of excess numerical dissipation, and not in period discrepancies.

 

 

B. Parabolic Initial Boundary Value Problems: the generalized trapezoidal family of finite difference time stepping algorithms is used which consist of the following equations:

 

 

 

 

where  is a parameter taken to be in the interval .  Unconditional stability requires that  be taken to be in the interval .  Maximal high-frequency numerical dissipation is provided by selecting .  Some well-known integrators are identified as follows:

 

Explicit forward Euler

 Crank Nicolson/midpoint rule

 Implicit backward Euler

 

C. Elliptic Boundary Value Problems: a backward finite difference (backward Euler) time stepping algorithms is used which consist of the following equations:

 

 

 

(3)     For implicit  time integration of hyperbolic IBVP, if , set internally to:

 

 

References / Bibliography

 

1.      Hilber, H.M., "Analysis and Design of Numerical Integration Methods in Structural Dynamics," Rep. No. EERC 76-29, Earthquake Engineering Research Center, University of California, Berkeley, CA, (1976).

 

2.      Hughes, T.J.R., Pister, K.S., and Taylor, R.L., "Implicit-Explicit Finite Elements in Nonlinear Transient Analysis," Comp. Meth. Appl. Mech. Eng., 17/18, (1979), 159-182.

 

3.            Newmark, N.M.,"A Method of Computation for Structural Dynamics," J. Eng. Mech. Div., ASCE, 85, EM3, (1959), 67-94.

 

 

Notes . .

 

 

 

 

Notes . .