RECOVER_ERROR
RECOVER_ERROR step_number = ns, etc....
Determine the magnitude of the error at any given time step.
Note Variable Name Type Default Description
(1) Element_group(s) string [none] Element group(s) for which the error is to
be
estimated. Name(s) must be enclosed in
quotation
marks.
Step_number integer [0] Step number at which error recovery is
to be
initiated.
Frequency integer [0] Error recovery frequency
EXAMPLE
Recover_error /
element_group(s) = "group_1", "group_2" /
step_number = 1 /
frequency = 1
Notes/
(1) List all element group names or numbers for which the error is to be estimated.
(2) The finite element provides an approximation to the exact solution of a mathematically well-posed problem. The difference between the exact and approximate solutions decreases as the size of the subdivision h gets smaller, or as the order of the interpolation polynomial functions used increases. In order to determine exactly the magnitude of the error at a given stage of subdivision the exact solution must be available, a situation not common in practice.
Error estimates can be obtained by projecting the field quantities onto the nodes to obtain a continuous field and by comparing the projected quantities with the elemental values, e.g., the error in stresses in continuum type problems defined as
(1)
where
= "exact
solution" and 
= "finite
element" stress, can be estimated with good accuracy as:
(2)
where
=
"projected" finite element stress.
The projection is performed by using the same interpolation functions as
used for representing the displacement field 
, viz.,
(3)
where
= vector of
nodal displacements, and N = nodal
interpolation function. Then
(4)
The
approximating equation is achieved by a weighted residual requirement for
equality between and and , viz.,
(5)
giving rise to the following matrix problem:
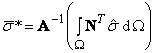(6)
where
(7)
The
above computation is made particularly simple if a lumped or diagonal
approximation is made to A by using
nodal quadrature. With both and fields available, the
error in stress can be estimated with good accuracy as:
(8)
The error computed in this manner is an a posterior error estimate, since it can only be computed after the solution of the problem has been obtained. The following error norms are computed:
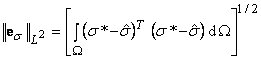= L2
norm of stress error (9)
= RMS error in stress (10)
These error norms are evaluated over the whole domain and over each finite element subdomain. We note that:
(11)
where
i refers to the individual finite element subdomains
. A posterior error
estimates can be used to refine the finite element approximation locally to
achieve results of a given desired accuracy economically and optimally. For that purpose, the error is projected onto
the nodes and may be displayed graphically.
Notes . .