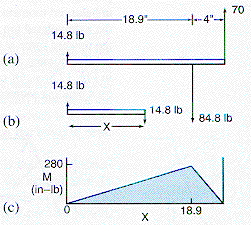
In this diagram the front fork is approximated by a straight tube of the same length and the normal forces acting on this tube are shown in diagram (a). The fork is in equilibrium at each point, and the bending moment at any location is computed as shown in (b). The magnitude of the moment is the product of the applied force and the distance of the measuring point from its line of action. Each section of the beam is treated as a free-body as illustrated in (b) and there can be no net force or moment acting on this free-body. This requires that the forces at each end are of the same magnitude and opposite direction, and that the remainder of the beam transfers a torque opposing that due to the force at the free end.
From: McMahon & Graham,
"The Bicycle & the Walkman,"
Merion (1992)
This moment increases from each end of the fork, having its maximum value at the point of junction with the down tube. Diagram (c) illustrates this, showing the moment due to the remainder of the beam in blue. At the free ends this moment is zero. This bending moment causes a stress in the fork which could cause deformation or buckling to occur.
| Structure |
| Menu |
| Prev |
| Next |