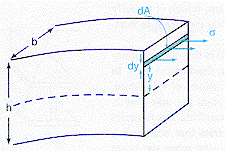
For a beam that has uniform properties (an isotropic material) and is symmetrical in cross section, an plane exists on which there is no stress or strain as a result of the bending.
This plane is the "neutral
axis" plane and the longitudinal stress due to the bending changes direction
as the plane is crossed. For the geometry of the diagram, the stress is
tensile at distances of radius greater than the neutral plane radius and compressive
for smaller radii . The stress, s, in the element
a distance, y, from the neutral axis i s proportional to the distance from
the axis and is given by:
s= E C y ,
where E is Young's modulus and C is the curvature, (1/ r), of the beam under
the action of the forces.
This stress makes a contribution to the bending
moment:
dM = s dA y = (E y /
r) (b dy) y = (E / r) { b y2 dy}
From: McMahon & Graham,
"The Bicycle & the Walkman,"
Merion (1992)
Each similar element in the material makes a corresponding contribution to the total bending moment, M, and M is determined by summing (integrating) all of these contributions as y goes from - h/2 to +h/2.
| Structure |
| Menu |
| Prev |
| Next |