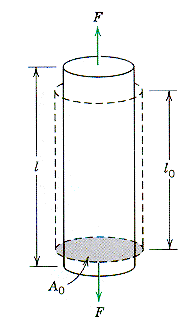
How a material responds to a load is best expressed in terms of the size independent quantities stress and strain. the diagram illustrates a cylindrical sample of initial area A₀ that is being loaded in tension by a force, F. As a result of the application of this force the sample changes from an initial unloaded length, L, to a final loaded length, L₀. In terms of these quantities, the stress is given by: s = F/A₀, and the associated strain by:       e = (L₀ - L)/L₀ = DL/L₀. These quantities are known as the Engineering Stress and the Engineering Strain.

In the elastic response range for the material being tested stress and strain are related through a material property known as an "Elastic Constant." For the tensile situation illustrated the elastic constant is known as Young's modulus and the elastic relationship is "Hooke's law." This is written:        s = E e. This linear relationship does not hold for all types of material. For example a rubber remains elastic over a very large range of strains but the slope of the stress-strain plot depends on the value of the strain. Materials that behave in this way are non-linear elastic materials and their elastic modulus E* = (ds/de) is strain dependent. The definition of E* used is for the "Tangent modulus" for the non-linear material.