Materials and Structure

For transverse loading of the composite, the components experience the same stress and for this isostress situation the total transverse strain of the composite is just the sum of the fiber strain and matrix strain. The strain is distributed between the components on the basis of their volume fraction so that the strain of the composite is given by:
e_C = e_FV_F + e_M(1 - V_F).
Combining this result with Hooke's Law gives the transverse Young's modulus:
E_C = (E_F E_M) / {E_F (1 - V_F) + E_MV_F}.
For this case also the value of Young's modulus can be controlled through the fiber volume fraction

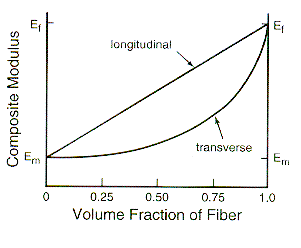
The lower diagram shows how the longitudinal and transverse values of the Composite Young's modulus depends on the fiber volume fraction. In a realistic material only volume fractions between 5% and 80% are of use.

From: McMahon and Graham:
"The Bicycle and the Walkman," Merion (1992)