|
A gear is a simple mechanical device that transmits rotational motion (force) to another gear or device. Gears are round and have teeth—linkages to mesh with other teeth—leading to a relatively slip-free transfer of movement. The amount of torque, speed, and direction of movement depends upon the gear’s design; function follows form in the transfer of forces in gears. |
|
|
|
Thus, the larger a gear’s radius, the slower its rotational speed. |
|
Gear Ratios |
|
Counting Teeth |
|
Forces in Gears |
|
Torque Ratio = (Radius A)/(Radius B) |
|
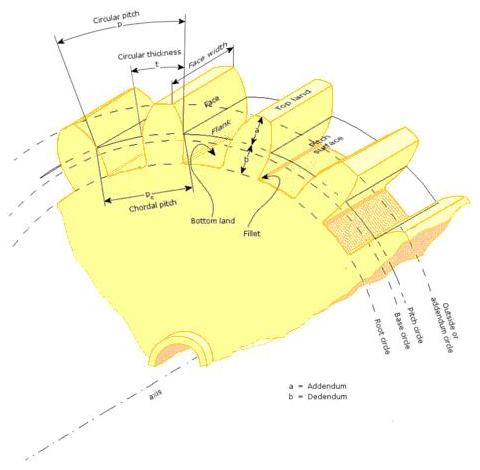
Useful Gear Nomenclature |
|
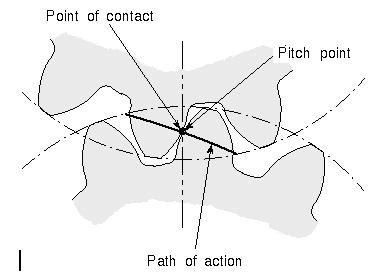
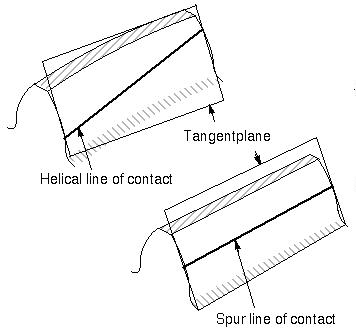
Line of Contact |
|
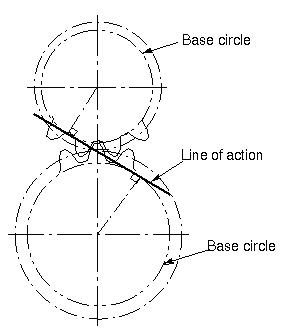
Line of Action |
|
Pitch Point |
|
Gears on Our EPICS Time Team Clock |
|
Sources: |
Written by Stephanie Bachas-Daunert'10