Lesson Plan - What's wrong with my clock?

EPICS Time Team Community Outreach
John Witherspoon Middle School
Engineering Club

Objective:
To encourage independent analytical thinking and engineering design through hands-on learning.
To address the mechanics of clocks.

Materials:
(Per Team of 3-4 Students)
1 K'Nex Model Clock
Various Parts Needed to Repair the Clock (e.g., gears, connectors, K'Nex pieces)

Procedure:
Form groups of 3 or 4 students each, preferably with varying levels of engineering skills and background.

Give brief introduction to the mechanics of clocks.
(10 minutes)

Have a visit from a "troubled CEO". There is a manufacturing defect in his clock factory; consequently, all of the recently-produced clocks are rife with problems -- hands on backwards, timing is incorrect, movement is backwards, etc. -- that (s)he cannot fix. The CEO asks the students to help, and hands each group a checklist and mission plan.
(5 minutes)

Work on the clocks, trying to fix the problems.
(30 minutes)

Assess the clocks' improvement and award prizes.
(15 minutes)

Troubled CEO Transcript:
Hi, I'm Handsy McClock, CEO of Cool Clocks, Inc. I am here on a very serious mission. There is something wrong at my factory... all of the clocks that we make aren't working right! I can't figure out the problems on my own, and I really need your help. Each group will get one clock to try to fix. Please, try your hardest! My company -- and all of the clock-lovers around the world -- are depending on you!

Clock Defects:
Each clock will have three defects, each of different difficulty to address.

Easy: the clock is moving in the counterclockwise direction, when it should be moving in a clockwise fashion
Solution: the face -- with arrows -- is on the wrong side of the clock. The face needs to be moved to the other side of the clock

Medium: make the clock move faster or slower
Solution: change the length of the pendulum
->Relationship between time and length of pendulum:
square_root(length) ~ time
(The square root of the pendulum length is directly proportional to the period - the actual formula is T = 2 pi square_root(I / (mgL)) so because there is an L^2 factor hidden in I, the formula can simplify to T ~ square_root(L), all else being invariant.)
So, if the pendulum length is changed by a factor of 2, the speed is changed by a factor of square root of 2. The main point: shorter pendulum is faster, while a longer pendulum is slower. The exact timing can be found via trial and error.

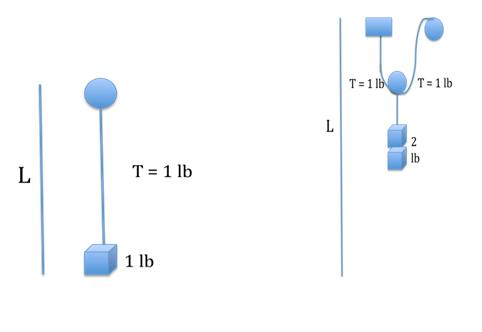
Hard (Complicated): double the time that the clock runs
Solution: a carriage needs to be inserted, the pendulum length must be doubled, and the weight must be doubled (see diagram)
->The carriage: a pulley support; the carriage must be able to roll because you always want the weight at the midpoint of the pendulum length
->In terms of energy: the clock must fall slower -- if it is running for double the time -- so, must add more weight to make it run more slowly.