---

1.7 Changing your Mind; Conditioning

 How should Q be related to P? The simplest answer goes by the name "conditioning" or "conditionalization":
 
 

Conditioning. Q(H) = P(H | D)
 
 

That means that your new unconditional probabilities will simply be your old conditional probabilities given D.

With H = D, the conditioning equation implies that your new judgmental probability for D is 1:
 
 

Certainty. Q(D) = 1
 
 

It also implies that your conditional probabilities given D will be the same, before and after the change:
 
 

Rigidity Relative to D (= Sufficiency of D)

 If H is any proposition, Q(H | D) = P(H | D)
 
 

Proof. Bythe quotient rule, Q(H | D) = Q(HD)/Q(D), = Q(HD) by the certainty condition, = P(HD | D) by the conditioning equation, = P(H | D) by the quotient rule.

 Not only are the certainty and rigidity conditions implied by conditioning; they also imply it:
 
 

Conditioning is equivalent to

certainty and rigidity--jointly.
 
 

Proof. By the quotient rule, the left-hand side of the rigidity condition = Q(HD)/Q(D), and by the certainty condition this = Q(HD) = Q(H).
 
 

It is important to note that certainty by itself is not enough to imply that Q comes from P by conditioning; the rigidity condition is also needed.

Example: the Green Bean. You reach into a bag for a jelly bean. It is surely grape-flavored if blue, but you know that the green ones are equally divided between lime and mint flavors, indistinguishable by touch. Thus P(Lime | Green) = P(Mint | Green) = 1/2, where P is your current probability function. Now you pull a bean out and see that it's green: Q(Green) = 1, where Q is your new probability function. Then the certainty condition holds, with D = Green. Still the rigidity condition needn't hold with that D, for you may know that among beans of the same shade of green as the one you pulled out, the mint flavor is twice as common as lime. Then Q(Mint) is 2/3, not 1/2 as the rigidity condition would suggest.
 
 

There are special circumstances under which the rigidity condition dependably holds. It would hold in the green bean example if D were reported to you by telegram, from an unimpeachable source that gave no hint of the shade, but just said "Green". Under such conditions you can be sure in advance that your new unconditional judgmental probabilities for the various flavors will be the same as your old conditional probabilities for those flavors, given the reported color. But that's because matters have been arranged so that you become certain of the color in a way that doesn't change your odds between the various shades, and therefore doesn't change your conditional probabilities for any hypotheses, given the color.

 That's an important point: rigidity relative to D is equivalent to the following condition.
 
 

Odds Form of Rigidity Relative to D.

Between propositions L and M that each imply D,

 posterior odds Q(L)/Q(M) = prior odds P(L)/P(M)
 
 

Proof of equivalence. Whether or not H implies D, the propositions DH (=L) and D (=M) both do. Then by the quotient rule, the odds form implies the other. Conversely, if the other form holds with H = L and with H = M, both of which imply D, then we have

 Q(L | D)       P(L | D)     Q(H)
----------  =  ---------- x ------  ,
 Q(M | D)       P(M | D)     Q(D)

Example: the Green Bean, again. If D is the hypothesis that the bean is green, and L and M are the hypotheses that the shade of green is the lime-looking and the mint-looking one, then after seeing that M is true your judgments will be Q(L)=0, Q(M)=1, whereas before the observation your judgments were P(L)=P(M). So the odds form of the rigidity condition fails because the prior odds P(L)/P(M) were even (=1), but the posterior odds Q(L)/Q(M) are 0.
 
 

---

1.8 Generalized Conditioning

Q(H | D) = P(H | D)

 Q(H | -D) = P(H | -D)
 
 

And initially you are unsure about D, i.e.,
 
 

0 < P(D) < 1
 
 

-- and so the same inequality holds for -D. But instead of becoming certain about D, your probability P(D) for it changes to some other non-extreme value:
 
 

Q(D) is neither 0 nor 1 nor P(D)
 
 

Now the required updating formula is easily obtained from the law of total posterior probability, in the form
 
 

Q(H) = Q(H | D)Q(D) + Q(H | -D)Q(-D)
 
 

Rewriting the two posterior conditional probabilities via the rigidity conditions, we have a version of the updating scheme, appropriate when the number of rigidity conditions is 2 (i.e., for D and -D, as above):
 
 

Generalized conditioning (n=2)

 Q(H) = P(H | D)Q(D) + P(H | -D)Q(-D)
 
 

More generally, with n incompatible alternatives D₁, D₂, etc., that exhaust the possibilities, the applicable rule of total probability has n terms on the right. If for each of these (say, the i'th) a rigidity condition holds, i.e.,
 
 

Q(H | Di) = P(H | Di),
 
 

then we have an updating scheme for any n = 2, 3, ... :
 
 

Generalized conditioning

 Q(H) = P(H | D₁)Q(D₁) + P(H | D₂)Q(D₂) + ...

Example 8.1 (n=3). Jane Doe is a histopathologist who hopes to settle on one of the following diagnoses on the basis of microscopic examination of a section of tissue surgically removed from a pancreatic tumor. She is sure that exactly one of the three is correct.

 D₁ = Islet cell carcinoma

 D₂ = Ductal cell carcinoma

 D₃ = Benign tumor

 In the event, examination does not drive her probability for any diagnosis to 1, but does fix her probabilities for the three candidates as follows.

 Q(D₁) = 1/3, Q(D₂) = 1/6, Q(D₃) = 1/2.

 Her conditional probabilities for the hypothesis H of 5 year survival given the diagnoses are unaffected by this examination:

 P(H | D₁) = Q(H | D₁) = .4
P(H | D₂) = Q(H | D₂) = .6
P(H | D₁) = Q(H | D₁) = .9

 Then by generalized conditioning, her posterior probability for 5 year survival will be

 (.4)(1/3) + (.6)(1/6) + (.9)(1/2) ~ .683,

 i.e., a weighted average of the values (.4, .6, .9) that Q(H) would have had if she had been sure of the three diagnoses -- the weights being her posterior probabilities for those diagnoses.
 
 

---

1.9 Bayes' Theorem

                     P(H)
P(H | D) = P(D | H) -----
                     P(D)

For many purposes this theorem is more usefully applied to odds than to probabilities. In particular, suppose there are two hypotheses, H and G, to which observational data D are relevant. If we consider only the odds between H and G the unconditional probability of D plays no role in the calculations:
 
 

Bayes' Theorem for Odds.
 
 

 P(H | D)     P(H)     P(D | H)
---------- = ------ x ----------
 P(G | D)     P(G)     P(D | G)

If you are conditioning on D, the ratio of P(D|H) to P(D|G) is what you can multiply your old odds by to get your new odds. It's called the Likelihood Ratio. Thus Bayes' theorem for odds says that when you change your mind by conditioning,
 
 

New Odds = Old Odds . Likelihood Ratio
 
 

Relevance. If you are conditioning on D, your new probabilities P(H|D) can obviously be obtained by multiplying your old probabilities P(H) by P(H|D)/P(H). Now by the quotient rule and the product rule we have
 
 

 P(H | D)       P(HD)      P(D | H)
---------- = ---------- = ----------
   P(H)       P(H)P(D)       P(D)

New Probability =

Old Probability . Relevance Quotient
 
 

Bayes' theorem is often quoted in a form attuned to cases in which you have clear probabilities P(F), P(G), etc., for mutually incompatible, collectively exhaustive hypotheses F, G, etc., and have clear conditional probabilities P(D|F), P(D|G), etc., for data D on each of them. Thus, for three such hypotheses F, G, H we have
 
 

Bayes' Theorem for Total Probabilities.
 
 

                      P(H)P(D|H)
P(H|D) = --------------------------------------
          P(F)P(D|F) + P(G)P(D|G) + P(H)P(D|H)

Example. Suppose a black ball is drawn, in the urn example, sec. 5. Was it more probably drawn from urn 1 or urn 2?

Solution. In Bayes' theorem for total probabilities, set H=H₁, G=H₂, and F=0. Then the term P(F)P(D|F) vanishes, and P(H₁|Black) will be the ratio of P(H₁)P(Black|H₁) = (1/3) (3/4) = 1/4 to the sum of that ratio with P(H₂)P(Black|H₂) = (2/3) (1/2) = 1/3. Then P(H₁|Black) is the ratio of 1/4 to 7/12, i.e., 3/7, so that P(H₂|Black) = 4/7. The odds are 4:3 on the black ball being drawn from urn 2.
 
 

---

1.10 Independence

Probabilistic Independence Defined. Two or more statements are independent (relative to P) iff the probability of joint truth of any selection of them is the product of the separate probabilities of truth.
 
 

Urns. Now suppose the hypotheses are that the first, second, etc. balls drawn from a certain urn will be winners -- i.e., green, say; the others are red. The urn contains N = m+n balls, of which n are green. After a ball is drawn it is replaced, and the contents of the urn mixed. Here, if you know what number n/N is, you are apt to regard the H's as equiprobable and independent: P(H_i) = n/N, P(H_iH_j) = (n/N)² if i and j are distinct, etc.

 But what if you don't know n/N in the urn example? In particular, suppose you're sure there are 10 balls in the urn, and you're sure that the number of winners among them is 3 or 7, but you don't know which, and you regard the two possibilities as equiprobable. By the rule of total probability we have
 
 

P(X) = P(X | 3)P(3) + P(X | 7)P(7)

 = P3(X)/2 + P7(X)/2
 
 

where at the right P3 and P7 are conditional probability functions: in general, PD(H) is another way of writing P(H | D). Relative to P3, and also relative to P7, the statements H₁, H₂,... are equiprobable and independent, for we have
 
 

P3(H₁)=P3(H₂)=.30, P3(H₁H₂)=.09,

 P7(H₁)=P7(H₂)=.70, P7(H₁H₂)=.49,
 
 

etc. Relative to P, the H's are equiprobable: setting X = H_i we have P(H_i) = .3/2+.7/2 = .5 for all i. But relative to P, the H's are dependent, e.g., because while independence requires that P(H₁H₂) = (.5)(.5) = .25, the figure we get by setting X = H₁H₂ is
 
 

P(H₁H₂) = .09/2 + .49/2 = .29
 
 

In drawing from an urn with unknown composition, outcomes of different drawings are judgmentally dependent on each other even though one judges that relative to the unknown truth of the matter (3 winners, or 7) different drawings are independent.

 We can put the matter so: relative to P, the H's are unconditionally dependent, but they are conditionally independent given each hypothesis about the real composition of the urn.
 
 

Definition. Conditional independence given

 H is probabilistic independence relative to PH.
 
 

Question. If A and B are conditionally independent given H, and also given -H, must they be simply independent?
 
 

---

1.11 "Real Probability"; Chance

 On one way of understanding the question the answer is surely "Yes"--but on that understanding our real probabilities retain judgmental components, so that you and I can have different real probabilities for one and the same hypothesis without neither of us being right, or wrong. (So in a sense, the answer is "No.") The idea: real probability is judgmental probability conditionally on the unknown true answers to various questions, which we may think of as combined into one long question:
 
 

"Real" probability for H relative to P and a question

 = P(H | the true answer)
 
 

Example 1. Longevity. Alma's real probability for Ben's living to age 65 is 3/4 or 3/5, depending on whether he smokes cigars or cigarettes:

 P(65 | cigars) = 3/4, P(65 | cigarettes) = 3/5.

 That comes from her knowledge of the mortality figures for men of Ben's age with the two habits, her certainty that he has one of them, and her ignorance of which.
 
 

Is this doubly relative definition of real probability the best we can do? Is there no absolute sense in which the real probability of rolling a six next with a certain loaded die might be (say) 10%, regardless of what our judgmental probabilities may be, and of what questions we think of?

 Suppose there is. A handy name for that is "chance." Suppose, then, that there is an unknown objective chance of a six turning up on the next toss of a certain die: one tenth, say.

 What sort of hypothesis is that? How could we find out whether it is true or false? There are puzzling questions about the hypothesis that the chance of H is p that don't arise regarding the hypothesis H itself.

 David Hume's skeptical answer to those questions says that chances are simply our projections of robust features of our judgmental probabilities from our minds out into the world--whence we hear them clamoring to be let back in. That's how our knowledge that the chance of H is p guarantees that our judgmental probability for H is p: the guarantee is really a presupposition. On Hume's analysis, the argument
 
 

(1) P(the chance of H is p) = 1, so P(H) = p
 
 

is valid because our conviction that the chance of H is p is a just a firmly felt commitment to p as our judgmental probability for H.
 
 

What if we are not sure what the chance of H is, but think it may be p? Here the relevant principle (2) specifies the probability of H on the condition that its chance is p:
 
 

(2) Homecoming. P(H | chance of H is p) = p unless p is excluded as a possible value, being in the interior of an interval we are sure does not contain the chance of H.
 
 

The "unless" clause rules out cases in which we are antecedently sure that the chance of H is not p because, for some chunk (... ) of the interval from 0 to 1, P(chance of H is inside the chunk) = 0:

 0------------^...p^......------1
 
 

Why isn't the "unless" clause simply the following?

 P(the chance of H is p) != 0

 That would be simpler, and might be realistic. But it would rule out certain mathematical models in which it seems natural to distribute the unit of probability smoothly across the unit interval so that every chunk gets positive probability but every point gets probability 0.
 
 

Example 2. The Uniform Distribution. The unit interval of points p (0<= p<1) is curled into a circle, an arrow pivoted at the center is spun, and you win $p, where p is the point where the arrow stops. For any particular chunk of the unit interval, the probability is positive that it will stop in it, but for any particular point the probability is 0 that it will stop there -- e.g., at p=1/4. But we cannot rule out all these point hypotheses, even though each has probability 0, for the probability is 1 that it will stop at some point.

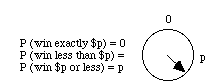
 Information making it unlikely that the chance of H is near p won't generally change your conditional probability for H, given that its chance is p.

Example 3. Hegemony. Although information that the last three balls drawn from an urn have all been green might be strong evidence for the hypothesis H that the next will will also be green, it would be overridden by further information that in the six draws before those last three no green balls were drawn. But evidence that 70% of the balls in the urn are green would not be overridden in that way. Even if P represents your judgment after seeing six reds followed by four greens, you'll judge that

 P(green next | the urn has 70% green) = 70%

 -- i.e., not 1/3, and not some compromise between 1/3 and 7/10. Of course, the past statistics might make you think the game dishonest, and so make you doubt that the chance of green next really is 70%, but that's another matter; your conditional probability for green next on the hypothesis that the chance is 70% will still be 70%.
 
 

According to homecoming, the condition `the chance of H is p' is hegemonic in the sense of overriding any other evidence represented in the probability function P--provided P(the chance of H is approximately p) != 0. But a specification of H's chance needn't override other conditions conjoined with it to the right of the bar. In particular, it won't override the hypothesis that H is true, or that H is false. Thus, since P(H | HC) = 1 when C is any condition consistent with H, P(H | H & the chance of H is .7) is 1, not .7; and that's no violation of hegemony.
 
 

On the Humean view the phrase "the chance of H is p" in the homecoming condition is just a place-holder for naural conditions in which the word "chance" does not appear, e.g., conditions specifying the composition of an urn.

Example 4. An urn contains 100 balls, of which an unknown number N are green. You are sure that if you knew N, your judgmental probability for a green ball's being drawn next would be N%:

 P(Green next | N of the hundred are green) = N%

 Then you take the chance of green next to be a physical magnitude, N/100, which you can determine empirically by counting. It is the fact that for you N satisfies the hegemony condition that identifies N% as the chance of drawing a green ball next, in your thinking.
 
 

This example was easy: an observable magnitude N/100 turned out to satisfy the hegemony condition for your probability function P, and so was identifiable as your idea of the chance of green next. Other problems are harder.

Example 4. The Loaded Die. Suppose H predicts ace on the next toss. Perhaps you are sure that if you understood the physics better, knowledge of the mass distribution in the die would determine for you a definite judgmental probability of ace next: if you knew the physics, then for some f it would be true that
 
 

P(Head next | The mass distribution is M) = f(M)
 
 

But you don't know the physics; in this case you know of no physical parameter f(M) that now satisfies the hegemony condition for your judgmental P.

 When we are unlucky in this way there may still be a point in speaking of the chance of H, i.e., of a yet-to-be-identified physical parameter that will be hegemonic for people in the future. Then in the hegemony condition we might read "the chance of H is p" as a place-holder for a still unknown physical description of what one day will be recognized as a hegemonic parameter. There's no harm in that, as long as we don't fool ourselves into thinking we already know it.
 
 

---

1.12 Problems

Result of X-ray Malignant (ca) Benign (be)

 Positive 0.792 0.096

 Negative 0.208 0.904
 
 

Here the conditioning propositions (ca, be) are at the top. If the physician's probabilistic judgment of the X-ray report is determined by the true- and false-positive rates as approximately
 
 

P(pos | ca)=.8, p(pos | be)=.1,
 
 

and her prior probability for cancer is determined by the statistics as P(ca)=.01, what will be her posterior odds P(ca | pos):P(be | pos) on malignancy?
 
 

2 The Taxicab Problem. "A cab was involved in a hit-and-run accident at night. Two cab companies, the Green and the Blue, operate in the city. You are given the following data:

 (a) 85% of the cabs in the city are Green, 15% are Blue.

 (b) A witness identified the cab as Blue. The court tested the reliability of the witness under the same circumstances that existed on the night of the accident and concluded that the witness correctly identified each one of the two colors 80% of the time and failed 20% of the time.

What is the probability that the cab involved in the accident was Blue rather than Green?"

Hint. 80% reliability means:

 P(Witness says X | X is true) = .8.
 
 

3 The Device of Imaginary Results--to help you identify your prior odds, e.g., "... that a man is capable of extra-sensory perception, in the form of telepathy. You may imagine an experiment performed in which the man guesses 20 digits (between 0 and 9) correctly. If you feel that this would cause the probability that the man has telepathic powers to become greater than 1/2, then the [prior odds] must be assumed to be greater than 10^-20. ... Similarly, if three consecutive correct guesses would leave the probability below 1/2, then the [prior odds] must be less than 10^-3." Derive these results.
 
 

4 The Rare Disease "You are suffering from a disease that, according to your manifest symptoms, is either A or B. For a variety of demographic reasons disease A happens to be 19 times as common as B. The two diseases are equally fatal if untreated, but it is dangerous to combine the respective appropriate treatments. Your physician orders a certain test which, through the operation of a fairly well understood causal process, always gives a unique diagnosis in such cases, and this diagnosis has been tried out on equal numbers of A- and B-patients and is known to be correct on 80% of those occasions. The tests report that you are suffering from disease B. Should you nevertheless opt for the treatment appropriate to A, on the supposition that the probability of your suffering from A is 19/23? Or should you opt for the treatment appropriate to B, on the supposition" ... "that the probability of your suffering from B is 4/5? It is the former opinion that would be irrational for you.. Indeed, on the other view, which is the one espoused in the literature, it would be a waste of time and money even to carry out the tests, since whatever their results, the base rates would still compel a more than 4/5 probability in favor of disease A. So the literature is propagating an analysis that could increase the number of deaths from a rare disease of this kind."

 Diaconis and Freedman (1981, pp. 333-4) suggest that Cohen is committing "the fallacy of the transposed conditional," i.e., he is confusing P(It is B | It is diagnosed as B), which is the number we're looking for, with P(It is diagnosed as B | It is B) = 80%, which is the true positive rate of the test for B.

 Use the odds form of Bayes' theorem to verify that if your prior odds on A are 19:1 and you take the true positive rate (for A, and for B) to be 80%, your posterior probability for A should be 19/23.
 
 

5 On the Credibility of Extraordinary Stories

 "There are, broadly speaking, two different ways in which we may suppose testimony to be given. It may, in the first place, take the form of a reply to an alternative question, a question, that is, framed to be answered by yes or no. Here, of course, the possible answers are mutually contradictory, so that if one of them is not correct the other must be so: -- Has A happened, yes or no?" ...

"On the other hand, the testimony may take the form of a more original statement or piece of information. Instead of saying, Did A happen? we may ask, What happened? Here if the witness speaks the truth he must be supposed, as before, to have but one way of doing so; for the occurrence of some specific event was of course contemplated. But if he errs he has many ways of going wrong" ...

(a) In an urn with 1000 balls, one is green and the rest are red. A ball is drawn at random and seen by no one but a slightly colorblind witness, who reports that the ball was green. What is your probability that the witness was right on this occasion, if his reliability in distinguishing red from green is .9, i.e., if P(He says it's X | It is X) = .9 when X = Red and when X = Green?

 (b) "We will now take the case in which the witness has many ways of going wrong, instead of merely one. Suppose that the balls were all numbered, from 1 to 1,000, and the witness knows this fact. A ball is drawn, and he tells me that it was numbered 25, what is the probability that he is right?" In answering you are to "assume that, there being no apparent reason why he should choose one number rather than another, he will be likely to announce all the wrong ones equally often."

Note. Reliability, r, is defined as the probability of the witness's speaking the truth, in the following sense.
 
 

P(Witness says it is n | It really is n) = r
 
 

6 The Three Prisoners. An unknown two will be shot, the other freed. Prisoner A asks the warder for the name of one other than himself who will be shot, explaining that as there must be at least one, the warder won't really be giving anything away. The warder agrees, and says that B will be shot. This cheers A up a little: his judgmental probability for being shot is now 1/2 instead of 2/3.

 Show (via Bayes theorem) that

 (a) A is mistaken - assuming that he thinks the warder is as likely to say "C" as "B" when he can honestly say either; but that

 (b) A would be right, on the hypothesis that the warder will say "B" whenever he honestly can.
 
 

7 The Two Children. You meet Max walking with a boy whom he proudly introduces as his son.

(a) What is your probability that his other child is also a boy, if you regard him as equally likely to have taken either child for a walk?

 (b) What would the answer be if you regarded him as sure to walk with the boy rather than the girl, if he has one of each?

 (c) What would the answer be if you regarded him as sure to walk with the girl rather than the boy, if he has one of each?
 
 

8 The Three Cards. One is red on both sides, one is black on both sides, and the other is red on one side and black on the other. One card is drawn and placed on a table. If a red side is up, what's the probability that the other side is red too?
 
 

9 Monty Hall. As a contestant on a TV game show, you are invited to choose any one of three doors and receive as a prize whatever lies behind it -- i.e., in one case, a car, or, in the other two, a goat. When you have chosen, the host opens a second door to show you a goat (there was bound to be one behind at least one of the others), and offers to let you switch your choice to the third door. Should you?
 
 

10 Causation vs. Diagnosis. "Let A be the event that before the end of the next year, Peter will have installed a burglar alarm in his home. Let B denote the event that Peter's home will have been burgled before the end of next year.

 "Question: Which of the two conditional probabilities, P(A | B) or P(A | -B), is higher?

"Question: Which of the two conditional probabilities, P(B | A) or P(B | -A), is higher?

 "A large majority of subjects (132 of 161) stated that P(A | B)>P(A | -B) and that P(B | A)<P(B | -A), contrary to the laws of probability."

 Substantiate this last remark by showing that the following is law of probability.

P(A | B) > P(A | -B) iff P(B | A) > P(B | -A)
 
 

11 Mixing. Prove that if AB=0, then P(C | AvB) must lie in the interval from P(C | A) to P(C | B).
 
 

12 Odds Factors. The "odds factor" for C given H is the factor by which your odds P(C)/P(-C) on C must be multiplied in order to get your odds on C given H, i.e., P(C | H)/P(-C | H). Suppose you take the chance of H to be p or p' , depending on whether or not C is true. What is your odds factor for C given H?
 
 

13 Conditioning: certainty is not enough

 The rigidity condition is generally overlooked, perhaps because of a lazy assumption that conditional probabilities are always stable. But clearly certainty alone is not enough. Here are two ways to see that.

 (a) If certainty sufficed, your probability function could never change. (Why?)

 (b) You draw a card at random from a normal deck and see that it is an ace. Then you are sure it is an ace -- but also that it is an ace or deuce. If certainty were enough, a contradiction would follow. (Why?)
 
 

14 Generalized Conditioning: Commutativity

 The end result of generalized conditioning twice, due to changes in your probabilities for D₁, D₂, ... and for E₁, E₂, ... , may well depend on the order of updating, even though the appropriate rigidity conditions hold. Illustrate that by a simple example.
 
 

---

1.13 Notes

Sec. 1.1 Question 4 is based on Nelson Goodman's "grue" paradox, in Fact, Fiction and Forecast: 4th ed., Harvard U. P., 1983, pp. 73-4.
 
 

Sec. 1.2 The set of real numbers from 0 to 1 is uncountable. This was proved by Georg Cantor (diagonal argument, 1895), as follows. Each number from 0 to 1 can be expressed as an endless decimal,

 0.d₁d₂d₃... ,

 (Where there is a choice, use the unterminating form, e.g., instead of .5, use .4999... .) Given any list of such endless decimals, Cantor identifies a decimal that is not on the list, i.e.

 0.e₁e₂e₃... ,

 where each digit en is d_n+1 or 0, depending on whether d_nis or is not less than 9. (For each n, en != d_n.) Since that "e" decimal does identify a number between 0 and 1, the "d" list cannot have been exhaustive.

 The view of Dutch book arguments as demonstrating actual inconsistency is Frank Ramsey's. So Brian Skyrms argues. The relevant paper of Ramsey's is "Belief and Probability," which is reprinted in Studies in Subjective Probability, 2nd ed., edited by Henry Kyburg, Jr. and Howard Smokler (Huntington, N.Y.: Robert E. Krieger, 1980).
 
 

Sec. 1.3 Problem 4 is from Amos Tversky and Daniel Kahneman's "Judgments of and by representativeness," which appears in a useful collection of articles edited by Daniel Kahneman, Paul Slovic, and Amos Tversky: Judgment Under Uncertainty (Cambridge U.P., 1982).
 
 

Sec. 1.4 The Dutch book argument for the product rule is due to Bruno de Finetti: see his "Foresight: Its Logical Laws and Subjective Sources," which is reprinted in the Kyburg and Smokler collection mentioned above.
 
 

Sec. 1.6 Lewis's trivialization result appeared in his "Probabilities of Conditionals and Conditional Probabilities": Philosophical Review85(1976)297-315. For subsequent developments, see Probabilities and Conditionals, Ellery Eells and Brian Skyrms (eds.): Cambridge University press, 1994 -- especially, the papers by Alan Há jek and Ned Hall.
 
 

Sec. 1.7, 8 I am responsible for the term "rigidity." The corresponding term in statistics is "sufficiency." For much more about all of this see Persi Diaconis and Sandy Zabell, "Updating subjective probability," Journal of the American Statistical Association 77(1982)822-830. For a little more, see "Some alternatives to Bayes's rule" by the same authors, in Information Pooling and Group Decision Making, Bernard Grofman and Guillermo Owen (eds.), JAI Press, Greenwich, Conn. and London, England, pp. 25-38.
 
 

Sec. 1.11 "Homecoming" is my cute name for what David Lewis calls "The Principal Principle" and Brian Skyrms calls "M"--for "Martingale".
 
 

Sec. 1.12, Problems

1 is from David M. Eddy's "Probabilistic reasoning in clinical medicine" in the Kahneman, Slovic, Tversky (1982) collection cited in the note on sec. 1.3 above.

2 is from pp. 156-7 of the Tversky and Kahneman article in that same collection.

3 is drawn from I. J. Good's pioneering book, Probability and the Weighing of Evidence: London, 1950, p. 35.

4 is from L. J. Cohen's "Can Human Irrationality be Experimentally Demonstrated?": The Behavioral and Brain Sciences 4(1981)317-331; see p. 329. The article is followed by various replies (of which one, by Persi Diaconis and David Freedman, pp. 333-4, is mentioned in problem 4) and they are followed by Cohen's rejoinder.

5 is adapted from pp. 409 ff. of John Venn's The Logic of Chance: 3rd ed., 1988 (reprinted 1962 by the Chelsea Publishing Co., N.Y.)

6-8 and others of that sort are discussed in a paper by Maya Bar-Hillel and Ruma Falk, "Some teasers concerning conditional probabilities," Cognition 11(1982)109-122.

10 is from p. 123 of the Kahneman, Slovik, Tversky (1982) collection cited in the note on sec. 1.3 above.
 
 

SOLUTIONS

2 41%

5 (a) 1/112 (b) r

7 (a) 1/2 (b) 1/3 (c) 1

8 2/3

9 Yes. (But why?)

11 Define Q as PAvB (sec 1.5). It obeys the law Q(C) = Q(C | A)Q(A) + Q(C | B)Q(B) of total probability. Note that Q(C | A) = P(C | A) and Q(C | B) = P(C | B). Then Q(C), an average of P(C | A) and P(C | B), must lie between them.

12 p/p'

13 If certainty sufficed, then

 (a) for any A, Q(A) = P(A | Av-A) = P(A).

 (b) Q(ace) = P(ace | ace) = 1, but also

 Q(ace) =P(ace | ace or deuce)= 1/2.

14 Suppose that D₁ = E₁ = it's sunny, and D₂ = E₂ = it is not sunny, and that two observations set your probability for E₁ at two different values. Then your final probability for E₁ will be determined by the second observation, no matter what value had been set by the first.