| Back to the Index |
 |
|
 |
Introduction
Huygens gave this account of the scientific method in the introduction to his Treatise on Light (1690):"... whereas the geometers prove their propositions by
fixed and incontestable principles, here the principles are verified by
the conclusions to be drawn from them; the nature of these things not allowing
of this being done otherwise. It is always possible thereby to attain a
degree of probability which very often is scarcely less than complete proof.
To wit, when things which have been demonstrated by the principles that
have been assumed correspond perfectly to the phenomena which experiment
has brought under observation; especially when there are a great number
of them, and further, principally, when one can imagine and foresee new
phenomena which ought to follow from the hypotheses which one employs,
and when one finds that therein the fact corresponds to our prevision.
But if all these proofs of probability are met with in that which I propose
to discuss, as it seems to me they are, this ought to be a very strong
confirmation of the success of my inquiry; and it must be ill if the facts
are not pretty much as I represent them."
Here we interpret and extend Huygens's methodology in
the light of the discussion of rigidity, conditioning, and generalized
conditioning in 1.7 and 1.8.
2.1 Confirmation
The thought is that you see an episode of observation, experiment, or reasoning as confirming or infirming a hypotheses depending on whether your probability for it increases or decreases during the episode, i.e., depending on whether your posterior probability, Q(H), is greater or less than your prior probability, P(H). The degree of confirmation
Q(H)-P(H)
can be a useful measure of that change--positive for confirmation,
negative for infirmation. Others are the probability factor, and
the odds factor, greater than 1 for confirmation, less than 1 for
infirmation:
Q(H) Q(H)/Q(-H) ------ ------------ P(H) P(H)/P(-H)These are the factors by which prior probabilities P(H) or odds P(H)/P(-H) are multiplied to get the posterior probabilities Q(H) or posterior odds Q(H)/Q(-H).
By the odds on one hypothesis against another
-- say, on a theory T, against an alternative S, is meant the ratio of
the probability of T to the probability of S. In these terms the plain
odds on T are simply the odds on T against -T. The definition of the odds
factor is easily modified for the case where S is not simply -T:
Q(T)/Q(S) Odds factor for T against S = ----------- P(T)/P(S)The odds factor can also be expressed as the ratio of the probability factor for T to that for S:
Q(T)/P(T) Odds factor for T against S = ----------- Q(S)/P(S)S is confirmed against T, or T against S, depending on whether the odds factor is greater than 1, or less.
We will choose among these measures case by case,
depending on which measure seems most illuminating.
2.2 Huygens on Light
Let H represent Huygens's principles and C the conclusions he drew from them--i.e., the conclusions which "verify" the principles.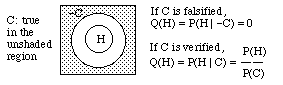
If C follows from H, and we can discover by observation whether C is true or false, then we have the means to test H -- more or less conclusively, depending on whether we find that C is false or true. If C proves false, H is refuted decisively, for then reality lies somewhere in the shaded region of the diagram, outside the "H" circle. If C proves true, H's probability changes from
area of "H" circle P(H) = -------------------- area of squareto
area of "H" circle P(H | C) = -------------------- area of "C" circleSo verification of C multiples H's probability by 1/P(C). Therefore it is the antecedently least probable conclusions whose unexpected verification raises H's probability the most. George Pólya put it: "More danger, more honor."
2.3 Observation and Sufficiency
It only remains to clarify the rationale for updating P to Q by conditioning on C or on -C , i.e., setting Q(H) = P(H | +/- C) depending on whether what we observe assures us of C's truth or of its falsity. According to the analysis in 1.7, the warrant for this must be rigidity (sufficiency) of truth or falsity of C as evidence about H, assuring us that whatever information the observation provides over and above a bare report of C's truth or falsity has no further relevance to H. This is guaranteed if the information about C arrives in a pre-arranged 1-word telegram: "true," or "false." But if the observers are the very people whose judgmental states are to be updated by the transition from P to Q, the possibility must be considered that the information about H conveyed by the observation will overflow the package provided by the sentence +/- C. Of course there will be no overflow if C is found
to be false, for since the shaded region is disjoint from the "H" circle,
any conditional probability function must assign 0 to H given falsity of
C. This guarantees rigidity relative to -C:
Q(H | -C) = P(H | -C) = 0
No matter what else observation might reveal about the circumstances of C's falsity, H would remain refuted.
But overflow is possible in case of a positive result, verification of C. In this case, observation may provide further information that complicates matters by removing our warrant to update by conditioning.
Example: the Green Bean, yet again.
H: the next bean will be lime-flavored.
C: the next bean will be green.
You know that half the beans in the bag are green,
all the lime-flavored ones are green, and the green ones are equally divided
between lime and mint flavors. So P(C) = 1/2 = P(H | C), and P(H) = 1/4.
But although Q(C) = 1, your probability Q(H) for lime can drop below P(H)=1/4
instead of rising to 1/2 = P(H | C) -- e.g. if, when you see that the bean
is green you also get a whiff of mint, or also see that it has a special
shade of green that you have found to be associated with the mint-flavored
ones.
2.4 Leverrier on Neptune
We now turn to a more recent methodological story. This is how Pólya tells it:"On the basis of Newton's theory, the astronomers tried
to compute the motions of ... the planet Uranus; the differences between
theory and observation seemed to exceed the admissible limits of error.
Some astronomers suspected that these deviations may be due to the attraction
of a planet revolving beyond Uranus' orbit, and the French astronomer Leverrier
investigated this conjecture more thoroughly than his colleagues. Examining
the various explanations proposed, he found that there was just one that
could account for the observed irregularities in Uranus' motion: the existence
of an extra-Uranian planet [sc., Neptune]. He tried to compute the orbit
of such a hypothetical planet from the irregularities of Uranus. Finally
Leverrier succeeded in assigning a definite position in the sky to the
hypothetical planet [say, with a 1
margin of error].
He wrote about it to another astronomer whose observatory was the best
equipped to examine that portion of the sky. The letter arrived on the
23rd of September 1846 and in the evening of the same day a new planet
was found within one degree of the spot indicated by Leverrier. It was
a large ultra-Uranian planet that had approximately the mass and orbit
predicted by Leverrier."
We treated Huygens's conclusion as a strict deductive consequence of his principles. But Pólya made the more realistic assumption that Leverrier's prediction C (a bright spot near a certain point in the sky at a certain time) was highly probable but not 100%, given his H (i.e., Newton's laws and observational data about Uranus). So P(C | H)~ 1; and presumably the rigidity condition was satisfied so that Q(C | H)~ 1, too. Then verification of C would have raised H's probability by a factor ~ 1/P(C), which is large if the prior probability P(C) of Leverrier's prediction was ~ 0.
Pólya offers a reason for regarding 1/P(C)
as at least 180 -- and perhaps as much as 13131: The accuracy of Leverrier's
prediction proved to be better than 1 , and the
probability of a randomly selected point on a circle or on a sphere being
closer than 1 to a previously specified point is
1/180 for a circle, and about 1/13131 for a sphere. Favoring the circle
is the fact that the orbits of all known planets lay in a common plane
("of the ecliptic"). Then the great circle cut out by that plane gets the
lion's share of probability. Thus, if P(C) is half of 1%, H's probability
factor will be about 200.
2.5 Multiple Uncertainties
In Pólya's story, Leverrier loosened Huygens's tight hypothetico-deductive reasoning by backing off from deductive certainty to values of P(C | H) falling somewhat short of 1 -- which he treated as approximately 1. But what is the effect of different shortfalls?Similarly, we can back off from observational certainty to Q(C) values less than 1. What if the confirming observation had raised the probability of Leverrier's C from a prior value of half of 1% to some posterior value short of 1; say, Q(C) = 95%. Surely that would that have increased H's probability by a factor smaller than Pólya's 200; but how much smaller?
Again, it would be more realistic to tell the story
in terms of a point prediction with stated imprecision -- say, +/- 1
. (In fact the new planet was observed within that margin, i.e., 57' from
the point.) As between two theories that make such predictions, the one
making the more precise prediction can be expected to gain the more from
a confirming observation. But how much more?
The following formula for H's probability
factor, with is due to John Burgess, answers such questions provided
C and -C satisfy the rigidity condition.
Q(C)-P(C) x P(C | H)-P(C) pf(H,C) = 1 + -------------------------- P(C)P(-C)By lots of algebra you can derive this formula from basic laws of probability and generalized conditioning with n=2 (sec. 1.8). If we call the term added to 1 in pf(H,C) the strength of confirmation for H in view of C's change in probability, then we have
Q(C)-P(C) x P(C | H)-P(C) sc(H,C) = ----------------------------- P(C)P(-C)The sign distinguishes confirmation (+) from infirmation (-, "negative confirmation").
Exercises. What does sc reduce to in these cases?
(a) Q(C)=1 (b) P(C | H)=1 (c) Q(C)=P(C | H)=1
(d) P(C) = 0 or 1, i.e., prior certainty about C.
To see the effect of precision, suppose that C predicts
that a planet will be found within +/- e of a certain point in the sky
--a prediction that is definitely confirmed, within the limits of observational
error. Thus P(C | H) = Q(C) = 1, and P(C) increases with e. Here sc(H,C)
= P(-C)/P(C) = the prior odds against C, and H's probability factor is
1/P(C). Thus, if it was thought certain that the observed position would
be in the plane of the ecliptic, P(C) might well be proportional to e,
P(C) = ke.
Exercise. (e) On this assumption of proportionality,
what happens to H's probability factor when e doubles?
2.6 Dorling on the Duhem problem
Skeptical conclusions about scientific hypothesis-testing are often drawn from the presumed arbitrariness of answers to the question of which to give up -- theory, or auxiliary hypothesis -- when they jointly contradict empirical data. The problem, addressed by Duhem in the first years of the 20th century, was agitated by Quine in mid-century. As drawn by some of Quine's readers, the conclusion depends on his assumption that aside from our genetical and cultural heritage, deductive logic is all we've got to go on when it comes to theory testing. That would leave things pretty much as Descartes saw them, just before the mid-17th century emergence in the hands of Fermat, Pascal, Huygens and others of the probabilistic ("Bayesian") methodology that Jon Dorling has brought to bear on various episodes in the history of science.The conclusion is one that scientists themselves generally dismiss, thinking they have good reason to evaluate the effects of evidence as they do, but regarding formulation and justification of such reasons as someone else's job -- the methodologist's. Here is an introduction to Dorling's work on the job, using extracts from his important but still unpublished 1982 paper.
It is presented here in terms of probability factors.
Assuming rigidity relative to D, the probability factor for a theory T
against an alternative theory S is the left-hand side of the following
equation. The right-hand side is called the likelihood ratio. The
equation follows from the quotient rule.
P(T | D)/P(S | D) P(D | T) ------------------ = ---------- P(T)/P(S) P(D | S)The empirical result D is not generally deducible or refutable by T alone, or by S alone, but in interesting cases of scientific hypothesis testing D is deducible or refutable on the basis of the theory and an auxiliary hypothesis A (e.g., the hypothesis that the equipment is in good working order). To simplify the analysis, Dorling makes an assumption that can generally be justified by appropriate formulation of the auxiliary hypothesis:
Prior independence
P(AT) = P(A)P(T), P(AS) = P(A)P(S)
In some cases S is simply the denial, -T, of T; in others it is a definite scientific theory R, a rival to T. In any case Dorling uses the independence assumption to expand the right-hand side of the odds Factor = Likelihood Ratio equation. Result, with f for odds factor:
P(D | TA)P(A) + P(D | T-A)P(-A) (1) f(T,S) = --------------------------------- P(D | SA)P(A) + P(D | S-A)P(-A)To study the effect of D on A, he also expands f(A,-A) with respect to T (and similarly with respect to S):
P(D | AT)P(T) + P(D | A-T)P(-T) (2) f(A,-A) = ----------------------------------- P(D | -AT)P(T) + P(D | -A-T)P(-T)
2.7 Einstein vs. Newton, 1919
In these terms Dorling analyzes two famous tests that were duplicated, with apparatus differing in seemingly unimportant ways, with conflicting results: one of the duplicates confirmed T against R, the other confirmed R against T. But in each case the scientific experts took the experiments to clearly confirm one of the rivals against the other. Dorling explains why the experts were right: "In the solar eclipse experiments of 1919, the telescopic
observations were made in two locations, but only in one location was the
weather good enough to obtain easily interpretable results. Here, at Sobral,
there were two telescopes: one, the one we hear about, confirmed Einstein;
the other, in fact the slightly larger one, confirmed Newton. Conclusion:
Einstein was vindicated, and the results with the larger telescope were
rejected." (
4)
Notation
T: General Relativistic light-bending effect of the sun
R: No light-bending effect of the sun
A: Both telescopes are working correctly
D: The actual, conflicting data from both telescopes
Set S=R in the odds factor (1), and observe that P(D | TA) = P(D | RA) = 0. Then (1) becomes
P(D | T-A) (3) f(T,R) = ------------ P(D | R-A)"Now the experimenters argued that one way in which A might easily be false was if the mirror of one or the other of the telescopes had distorted in the heat, and this was much more likely to have happened with the larger mirror belonging to the telescope which confirmed R than with the smaller mirror belonging to the telescope which confirmed T. Now the effect of mirror distortion of the kind envisaged would be to shift the recorded images of the stars from the positions predicted by T to or beyond those predicted by R. Hence P(D | T-A) was regarded as having an appreciable value, while, since it was very hard to think of any similar effect which could have shifted the positions of the stars in the other telescope from those predicted by R to those predicted by T, P(D | R-A) was regarded as negligibly small, hence the result as overall a decisive confirmation of T and refutation of R." (
4) Thus in (3) we have f(T,R) >> 1.
2.8 Bell's Inequalities: Holt vs. Clauser
"Holt's experiments were conducted first and confirmed the predictions of the local hidden variable theories and refuted those of the quantum theory. Clauser examined Holt's apparatus and could find nothing wrong with it, and obtained the same results as Holt with Holt's apparatus. Holt refrained from publishing his results, but Clauser published his, and they were rightly taken as excellent evidence for the quantum theory and against hidden-variable theories." ( 4)
Notation
T: Quantum theory
R: Disjunction of local hidden variable theories
A: Holt's setup is sensitive enough to
distinguish T from R
D: The specific correlations predicted by T and
contradicted by R are
not detected by Holt's setup
The characterization of D yields the first two of the
following equations. In conjunction with the characterization of A it also
yields P(D | T-A) = 1, for if A is false, Holt's apparatus was not sensitive
enough to detect the correlations that would have been present according
to T; and it yields P(D | R-A) = 1 because of the wild improbability of
the apparatus "hallucinating" those specific correlations.
P(D | TA) = 0, P(D | RA) = 1,
P(D | T-A) = P(D | R-A) = 1
Setting S=R in (1), these substitutions yield
(4) f(T,R) = P(-A)Then with a prior probability 4/5 for adequate sensitivity of Holt's apparatus, the odds between quantum theory and the local hidden variable theories shift strongly in favor of the latter, e.g., with prior odds 45:55 between T and R, the posterior odds are only 9:55, a 14% probability for T.
Why then does not Holt publish his result? Because
the experimental result undermined confidence in his apparatus. Setting
-T = R in (2) because T and R were the only theories given any credence
as explanations of the results, and making the same substitutions as in
(4), we have
(5) f(A,-A) = P(R)so the odds on A fall from 4:1 to 2.2:1; the probability of A falls from 80% to 69%. Holt is not prepared to publish with better than a 30% chance that his apparatus could have missed actual quantum mechanical correlations; the swing to R depends too much on a prior confidence in the experimental setup that is undermined by the same thing that caused the swing.
Now why did Clauser publish?
Notation
T: Quantum theory
R: Disjunction of local hidden variable theories
C: Clauser's setup is sensitive enough
E: The specific correlations predicted by T and
contradicted by R are detected by Clauser's setup
Suppose that P(C) = .5. At this point, although P(A) has
fallen by 11%, both experimenters still trust Holt's well-tried set-up
better than Clauser's. Suppose Clauser's initial results E indicate presence
of the quantum mechanical correlations pretty strongly, but still with
a 1% chance of error. Then E strongly favors T over R:
P(E | TC)P(C)+P(E | T-C)P(-C) (6) f(T,R) = ------------------------------- P(E | RC)P(C)+P(E | R-C)P(-C) .5 + .01 + .5 = --------------- = 50.5 .01Starting from the low 9:55 to which T's odds fell after Holt's experiment, odds after Clauser's experiment will be 909:110, an 89% probability for T.
The result E boosts confidence in Clauser's apparatus
by a factor of
P(E | CT)P(T) + P(E | CR)P(R) (7) f(C,-C) = --------------------------------- = 15 P(E | -CT)P(T) + P(E | -CR)P(R)This raises the initially even odds on C to 15:1, raises the probability from 50% to 94%, and lowers the 50% probability of the effect's being due to chance down to 6 or 7 percent.
2.9 Laplace vs. Adams
Finally, note one more class of cases: a theory T remains highly probable although (with auxiliary hypothesis A) it implies a false prediction D. With S=-T in formulas (1) and (2), with P(D | TA)=0, and settingP(D | T-A) P(D | -TA) t = ------------- s = ------------ P(D | -T-A) P(D | -T-A)we have
t (8) f(T,-T) = ----------------- sP(A)/P(-A) + 1 s (9) f(A,-A) = ----------------- tP(T)/P(-T) + 1 tP(-A) (10) f(T,-A) = -------- sP(-T)These formulas apply to (
1) "a famous
episode from the history of astronomy which clearly illustrated striking
asymmetries in `normal' scientists' reactions to confirmation and refutation.
This particular historical case furnished an almost perfect controlled
experiment from a philosophical point of view, because owing to a mathematical
error of Laplace, later corrected by Adams, the same observational data
were first seen by scientists as confirmatory and later as disconfirmatory
of the orthodox theory. Yet their reactions were strikingly asymmetric:
what was initially seen as a great triumph and of striking evidential weight
in favour of the Newtonian theory, was later, when it had to be re-analyzed
as disconfirmatory after the discovery of Laplace's mathematical oversight,
viewed merely as a minor embarrassment and of negligible evidential weight
against the Newtonian theory. Scientists reacted in the `refutation' situation
by making a hidden auxiliary hypothesis, which had previously been considered
plausible, bear the brunt of the refutation, or, if you like, by introducing
that hypothesis's negation as an apparently ad hoc face-saving auxiliary
hypothesis."
Notation
T: the theory, Newtonian celestial mechanics
A: The hypothesis that disturbances (tidal friction, etc.) make a negligible contribution to
D: the observed secular acceleration of the moon.
Dorling argues on scientific and historical grounds for
approximate numerical values
t=1, s=1/50
The general drift: t = 1 because with A false, truth or falsity of T is irrelevant to D, and t = 50s because in plausible partitions of -T into rival theories predicting lunar accelerations, P(R | -T) = 2% where R is the disjunction of rivals not embarrassed by D.
Then for a theorist whose odds are 3:2 on A and
9:1 on T (probabilities 60% for A and 90% for T),
f(T,-T)=100/103, f(A,-A)=1/500, f(T,A)=200.
Thus the prior odds 900:100 on T barely decrease, to 900:103;
the new probability of T, 900/1003, agrees with the original 90% to two
decimal places. But odds on the auxiliary hypothesis A drop sharply, from
prior 3:2 to posterior 3/1000, i.e., the probability of A drops from 60%
to about three tenths of 1%.
2.10 Dorling's conclusions
"Until recently there was no adequate theory available of how scientists should change their beliefs in the light of evidence. Standard logic is obviously inadequate to solve this problem unless supplemented by an account of the logical relations between degrees of belief which fall short of certainty. Subjective probability theory provides such an account and is the simplest such account that we possess. When applied to the celebrated Duhem (or Duhem-Quine) problem and to the related problem of the use of ad hoc, or supposedly ad hoc, hypotheses in science, it yields an elegant solution. This solution has all the properties which scientists and philosophers might hope for. It provides standards for the validity of informal deductive reasoning comparable to those which traditional logic has provided for the validity of informal deductive reasoning. These standards can be provided with a rationale and justification quite independent of any appeal to the actual practice of scientists, or to the past success of such practices. [Here a long footnote explains the Putnam-Lewis Dutch book argument for conditioning.] Nevertheless they seem fully in line with the intuitions of scientists in simple cases and with the intuitions of the most experienced and most successful scientists in trickier and more complex cases. The Bayesian analysis indeed vindicates the rationality of experienced scientists' reactions in many cases where those reactions were superficially paradoxical and where the relevant scientists themselves must have puzzled over the correctness of their own intuitive reactions to the evidence. It is clear that in many such complex situations many less experienced commentators and critics have sometimes drawn incorrect conclusions and have mistakenly attributed the correct conclusions of the experts to scientific dogmatism. Recent philosophical and sociological commentators have sometimes generalized this mistaken reaction into a full-scale attack on the rationality of men of science, and as a result have mistakenly looked for purely sociological explanations for many changes in scientists' beliefs, or the absence of such changes, which were in fact, as we now see, rationally de rigeur. "It appears that in the past even many experts have
sometimes been misled in trickier reasoning situations of this kind. A
more widespread understanding of the adequacy and power of the kinds of
Bayesian analyses illustrated in this paper could prevent such mistakes
in the future and could form a useful part of standard scientific education.
It would be an exaggeration to say that it would offer a wholly new level
of precision to informal scientific reasoning, for of course the quantitative
subjective probability assignments in such calculations are merely representative
surrogates for informal qualitative judgments. Nevertheless the qualitative
conclusions which can be extracted from these relatively arbitrary quantitative
illustrations and calculations seem acceptably robust under the relevant
latitudes in those quantitative assignments. Hence if we seek to avoid
qualitative errors in our informal reasoning in such scientific contexts,
such illustrative quantitative analyses are an exceptionally useful tool
for ensuring this, as well as for making explicit the logical basis for
those qualitative conclusions which follow correctly from our premises,
but which are sometimes nevertheless surprising and superficially paradoxical."
( 5)
2.11 Problems
1 "Someone is trying decide whether or not T is true. He notes that T is a consequence of H. Later he succeeds in proving that H is false. How does this refutation affect the probability of T?" In particular, what is P(T)-P(T|~ H)?2 "We are trying to decide whether or not T is
true. We derive a sequence of consequences from T, say C1, C2,
C3, ... . We succeed in verifying C1, then C2,
then C3, and so on. What will be the effect of these successive
verifications on the probability of T?" In particular, setting P(T|C1&C2&...
Cn-1&Cn) = pn, what is the probability
factor pn/pn+1?
3 Four Fallacies. Each of the following plausible rules is unreliable. Find counterexamples to (b), (c), and (d) on the model of the one for (a) given below.
(a) If D confirms T, and T implies H, then D confirms H. Counterexample: in an eight-ticket lottery, let D mean that the winner is ticket 2 or 3, T that it is 3 or 4, H that it is neither 1 nor 2.
(b) If D confirms H and T separately, it must confirm their conjunction, T&H.
(c) If D and E each confirm H, then their conjunction, E&F, must also confirm H.
(d) If D confirms a conjunction, T&H, then it
can't infirm each conjunct separately.
2.12 Notes
Sec. 2.1. The term "Bayes factor" or simply "factor" is more commonly used than "odds factor". Call it `f'. A useful variant is its logarithm, sc., the weight of evidence for T against S:w(T, S) = log f(T, S)
As the probability factor varies from 0 through 1 to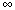 
, its logarithm varies from - 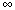through 0 to +
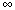, thus equalizing the treatments of confirmation and infirmation. Where
the odds factor is multiplicative for odds, weight of evidence is additive
for logarithms of odds (`lods'):
(new odds) = f . (old odds)
log(new odds) = w + log(old odds)
Sec. 2.2: "More danger, more honor." See George Pólya,
Patterns of Plausible Inference, 2nd ed., Princeton University Press
1968, vol. 2, p. 126.
Sec. 2.4. See Pólya, op. cit., pp. 130-132.
Sec. 2.6. See Jon Dorling, "Bayesian personalism, the methodology of research programmes, and Duhem's problem" Studies in History and Philosophy of Science 10(1979)177-187.
More along the same lines: Michael Redhead, "A Bayesian reconstruction of the methodology of scientific research programmes," Studies in History and Philosophy of Science 11(1980)341-347.
Dorling's unpublished paper from which excerpts
appear here in sec. 2.7 - 2.10 is "Further illustrations of the Bayesian
solution of Duhem's problem" (29 pp., photocopied, 1982). References here
(" 4" etc.) are to the numbered sections of that
paper.
Dorling's work is also discussed in Colin Howson
and Peter Urbach,
Scientific Reasoning: the Bayesian approach (Open
Court, La Salle, Illinois, 2nd ed., 1993).
Sec. 2.10, the Putnam-Lewis Dutch book argument (i.e.,
for conditioning as the only legitimate updating policy). Putnam stated
the result, or, anyway, a special case, in a 1963 Voice of America Broadcast,
"Probability and Confirmation", reprinted in his Mathematics, Matter
and Method, Cambridge University Press (1975)293-304. Paul Teller,
"Conditionalization and observation", Synthese 26(1973)218-258,
reports--and attributes to David Lewis--a general argument to that effect
which Lewis had devised as a reconstruction of what Putnam must have had
in mind.
Sec. 2.11. Problems 1 and 2 are from George Pólya,
"Heuristic reasoning and the theory of probability", American Mathematical
Monthly48(1941)450-465. Problem 3 relates to Carl G. Hempel's
"Studies in the logic of confirmation", Mind 54(1945)1-26
and 97-121. Reprinted in Hempel's Aspects of Scientific Explanation,
The Free Press, New York, 1965.
| Back to the Index |
|
|
|
Please write to bayesway@princeton.edu with any comments or suggestions.