Introduction

4.1 Preference Logic

 In fact, they took your utilities for states of nature to be the same, no matter which option you choose, as when states of nature determine definite dollar gains or losses, and these are all you care about. This condition may seem overly restrictive, for the means by which gains are realized may affect your final utility -- as when you prefer work to theft as a chancy way of gaining $1000 (success) or $0 (failure). But the condition can always be met by making distinctions, e.g., by splitting each state of nature in which you realize an outcome by work-or-theft into one in which you realize it by work, and another in which you realize it by theft. (The difference between the work and theft options will be encoded in their associated probability distributions: each assigns probability 0 to the set of states in which you opt for the other.) This means taking a naturalistic view of the decision-maker, whose choices are blended with states of nature in a single space, 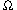 ; each point 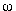 in that space represents a particular choice by the decision-maker as well as a particular state of (the rest of) nature.

 In 1965 Bolker and Jeffrey offered a framework of that sort in which options are represented by propositions (i.e., subsets of 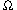 : in statistical jargon, "events"), and any choice is a decision to make some proposition true. Each such proposition corrsponds to a definite probability distribution in the von Neumann-Morgenstern scheme. To the option of making the proposition A true corresponds the conditional probability distribution P(--| A), where the unconditional distribution P(--) represents your prior probability judgment -- i.e., prior to deciding which option-proposition to make true. And your expectation of utility associated with the A-option will be your conditional expectation of utility, E(u | A) -- also known as your desirability for truth of A, and denoted "des A":
 
 

des A = E(u | A)
 
 

Now preference (>), indifference (=), and preference-or-indifference (>= ) go by desirability, so that
 
 

A>B if des A > des B

 A=B if des A = des B

 A>= B if des A >= des B
 
 

Note that it is not only option-propositions that appear in preference rankings; you can perfectly well prefer a sunny day tomorrow (= truth of "Tomorrow will be sunny") to a rainy one even though you know you cannot affect the weather.

 Various principles of preference logic can now be enunciated, and fallacies identified, as in the following two examples. The first is a fallacious mode of inference according to which you must prefer B's falsity to A's if you prefer A's truth to B's:
 
 

              A > B
Invalid:    ---------
             -B > -A

        case:            tt      tf       ft     ff
        P(case):        .33     .33      .01    .33
        des(case):        0       1     -100     10

            A >= B
Valid: ---------------- (if A and B are incompatible)
        A >=  AvB >= B.

 Bayesian decision theory is said to represent a certain structural concept of rationality. This is contrasted with substantive criteria of rationality having to do with the aptness of particular probability and utility functions to particular predicaments. With Davidson, I would interpret this talk of rationality as follows. What remains when all substantive questions of rationality are set aside is bare logic, a framework for tracking your changing judgments, in which questions of validity and invalidity of argument-forms can be settled as illustrated above. A complete set of substantive judgments would be represented by a Bayesian frame, consisting of (1) a probability distribution over a space 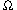 of "possible worlds," (2) a function u assigning "utilities" to the various worlds in 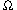 , and (3) an assignment of subsets of 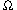 as values to letters "A", "B", etc., where the letters represent sentences and the corresponding subsets represent "propositions." In any logic, validity of an argument is truth of the conclusion in every frame in which all the premises are true. In a Bayesian logic of decision, Bayesian frames represent possible answers to substantive questions of rationality; we can understand that without knowing how to determine whether particular frames would be substantively rational for you on particular occasions. So in Bayesian decision theory we can understand validity of an argument as truth of its conclusion in any Bayesian frame in which all of its premises are true, and understand consistency of a judgment (e.g., affirming A > B while denying -B > -A), as existence of a non-empty set of Bayesian frames in which the judgment is true. On this view, consistency -- bare structural rationality -- is simply representability in the Bayesian framework.
 
 
 

4.2 Kinematics

¹In choosing a mixed option -- in which you choose one two options, O₁ or O₂, depending on whether some proposition C is true or false -- you place the following constraint on your probabilities.
 
 

Stable conditional probabilities

 P(O₁ | C) and P(O₂ | -C) are set near 1
 
 

(Near: you may mistake C's truth value, or bungle an attempt to make O_i true, or revise your decision.) As choosing the mixed option involves expecting to learn whether C is true or false, choosing it involves expecting your probabilities for C and -C to move toward the extremes:
 
 

Labile probabilities of conditions

 P(C) and P(-C) change from middling

 values to extreme values, near 0 or 1
 
 

This combination of stable conditional probabilities and labile probabilities of conditions is analogous to the constraints under which modus ponens (below) is a useful mode of inference; for if confidence in the second premise is to serve as a channel transmitting confidence in the first premise to the conclusion as well, the increase in P(first premise) had better not be accompanied by a decrease in P(second premise).
 
 

                    C
               D or not C
Modus Ponens  ------------
                    D

a = P(A | C), a' = P(A | -C), o = P(C)/P(-C)
 
 

and suppose a and a' both remain fixed as the odds o on C change. Then P(C | A) and P(C | -A) must change, since
 
 

                a                        a' 
P(C | A) = -----------   P(C | -A) = ---------
            a + a' /o                 a' + ao

Example. One day on Broadway, my wife and I saw what proved to be Mayor Dinkins. There were various clues: police, cameramen, etc. We looked, and smiled tentatively. He came and shook hands. Someone gave us Dinkins badges. We had known an election was coming and the candidates campaigning. At the end we had no doubt it was the Mayor. But there was no thought of describing the sensations on which our progress toward conviction was founded, no hope of formulating sensory data propositions that brought our probabilities up the unit interval toward 1:
 
 

P_old(It's Dinkins)

 P_old(It's Dinkins | data1)

 P_old(It's Dinkins | data1 & data2)

 ...

Of course the people in uniform and the slight, distinguished figure with the moustache might all have been actors. Our visual, auditory and tactile experiences did combine with our prior judgments to make us nearly certain it was the Mayor, but there seems to be no way to represent that process by conditioning on data propositions that are sensory certainties. The accessible data propositions were chancy claims about people on Broadway, not authoritative reports of events on our retinas, palms, and eardrums. We made reasonable moves (smiling, shaking the hand) on the basis of relatively diffuse probability distributions over a partition of such chancy propositions -- distributions not obtained by conditioning their predecessors on fresh certainties. (Jeffrey 1992 1-13, 78-82, etc.)

 Here are two generalizations of conditioning that you can prove are applicable in such cases, provided rigidity conditions hold for a partition { C₁, C₂, ... } of  .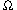
 
 

If the conditions Q(A | C_i) = P(A | C_i) all hold,

 then probabilities and factors can be updated so:
 
 

(Probabilities) Q(A) = 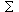 _iP(C_i)Q(A | C_i)

(Factors) f(A) = 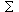 if(C_i)P(C_i | A)

 In the second condition, f(A) and f(C_i) are the factors Q(A)/P(A) and Q(C_i)/P(C_i) by which probabilities P(A), P(C_i) are multiplied in the updating process.
 
 

Generalized conditioning allows probabilistic response to observations which prompt no changes in your conditional probabilities given any of the C_i but do prompt definite new probabilities or factors for the C_i. (If your new probability for one of the C_i is 1, this reduces to ordinary conditioning.)

 Probabilistic judgment is not generally a matter of assigning definite probabilities to all propositions of interest, any more than yes/no judgment is a matter of assigning definite truth values to all of them. Typical yes/no judgment identifies some propositions as true, leaving truth values of others undetermined. Similarly, probabilistic judgment may assign values to some propositions, none to others.

 The two sorts of generalized conditioning tolerate different sorts of indefiniteness. The probability version determines a definite value for prnew(A) even if you had no old probabilities in mind for the C_i, as long as you have definite new values for them and definite old values for A conditionally on them. The factor version, determining the probability ratio f(A), tolerates indefiniteness about your old and new probabilities of A and of the C_i as long as your prold(C_i | A) values are definite. Both versions illustrate the use of dynamic constraints to represent probabilistic states of mind. In the next section, judgments of causal influence are analyzed in that light.
 
 
 

4.3 Causality

 Is there something about your judgmental probabilities which shows that you are treating truth of one proposition as promoting truth of another -- rather than as promoted by it or by truth of some third proposition which also promotes truth of the other? Here the promised positive answer to this question is used to analyze puzzling problems in which we see acts as mere symptoms of conditions we would promote or prevent if we could. Such "Newcomb problems" (Nozick 1963, 1969, 1990) pose a challenge to the decision theory floated in the first edition of The Logic of Decision (Jeffrey 1965), where notions of causal influence play no rô le. The present suggestion about causal judgments will be used to question the credentials of Newcomb problems as decision problems.

 The suggestion (cf. Arntzenius) is that imputations of causal influence are not shown simply by momentary features of probabilistic states of mind, but by intended or expected features of their evolution. The following is a widely recognized probabilistic consequence of the judgment that truth of one proposition ("cause") promotes truth of another ("effect").
 
 

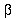>0 P(effect | cause) - P(effect | -cause) > 0
 
 

But what distinguishes cause from effect in this relationship? -- i.e., a relationship equivalent to
 
 

P(cause | effect) - P(cause | -effect) > 0
 
 

With Arntzenius, I suggest the following answer, i.e., rigidity relative to the partition { cause, -cause} .
 
 

Rigidity Constancy of P(effect | cause) and

 P(effect | -cause) as P(cause) varies
 
 

Both 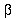 >0 and rigidity are conditions on a variable "p_r" ranging over a set of probability functions. The functions in the set represent ideally definite momentary probabilistic states of mind for the deliberating agent. Clearly, p_r can vary during deliberation, for if deliberation converges toward choice of a particular act, the probability of the corresponding proposition will rise toward 1. In general, agents's intentions or assumptions about the kinematics of p_r might be described by maps of possible courses of evolution of probabilistic states of mind -- often, very simple maps. These are like road maps in that paths from point to point indicate feasibility of passage via the anticipated mode of transportation, e.g., ordinary automobiles, not "all terrain" vehicles. Your kinematical map represents your understanding of the dynamics of your current predicament, the possible courses of development of your probability and desirability functions.

The Logic of Decision used conditional expectation of utility given an act as the figure of merit for the act, sc., its desirability, des(act). Newcomb problems (Nozick 1969) led many to see that figure as acceptable only on special causal assumptions, and a number of versions of "causal decision theory" were proposed as more generally acceptable. In the one I like best (Skyrms 1980), the figure of merit for choice of an act is the agent's unconditional expectation of its desirability on various incompatible, collectively exhaustive causal hypotheses. But if Newcomb problems are excluded as bogus, then in genuine decision problems des(act) will remain constant throughout deliberation, and will be an adequate figure of merit.

 In any decision problem whose outcome is not clear from the beginning, probabilities of possible acts will vary during deliberation, for finally an act will be chosen and so have probability near 1, a probability no act had initially. Newcomb problems (Table 1) seem ill posed as decision problems because too much information is given about conditional probabilities, i.e., enough to fix the unconditional probabilities of the acts. We are told that there is an association between acts (making A true or false) and states of nature (truth or falsity of B) which makes acts strong predictors of states, and states of acts, in the sense that p and q are large relative to p' and q' -- the four terms being the agent's conditional probabilities:.

p = P(B | A), p' = P(B | -A),

 q = P(A | B), q' = P(A | -B)
 
 

But the values of these terms themselves fix the agent's probability for A, for they fix the odds on A as

   P(A)         qp' 
---------- = --------
  P(~ A)      (1-q)p

4.4 Fisher

For smokers who see quitting as prophylaxis against cancer, preferability goes by initial des(act) as in Table 1b; but there are views about smoking and cancer on which these preferences might be reversed. Thus, R. A. Fisher (1959) urged serious consideration of the hypothesis of a common inclining cause of (A) smoking and (B) bronchial cancer in (C) a bad allele of a certain gene, posessors of which have a higher chance of being smokers and developing cancer than do posessors of the good allele (independently, given their allele). On that hypothesis, smoking is bad news for smokers but not bad for their health, being a mere sign of the bad allele, and, so, of bad health. Nor would quitting conduce to health, although it would testify to the agent's membership in the low-risk group.

 On Fisher's hypothesis, where +/- A and +/- B are seen as independently promoted by +/- C, i.e., by presence (C) or absence (-C) of the bad allele, the kinematical constraints on p_r are the following. (Thanks to Brian Skyrms for this.)
 
 

Rigidity The following are constant as c = P(C) varies.

 a = P(A | C) a' = P(A | -C)

 b = P(B | C) b' = P(B | -C)
 
 

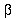>0 P(B | A) > P(B | -A), i.e., p > p
 
 

Indeterminacy None of a, b, a' , b' are 0 or 1.
 
 

Independence P(AB | C) = ab, P(AB | -C) = a' b'

Since in general, P(F | GH) = P(FG | H)/P(G | H), the independence and rigidity conditions imply that +/- C screens off A and B from each other, in the following sense.
 
 

Screening-off P(A | BC) = a, P(A | B-C) = a'

P(B | AC) = b, P(B | A-C) = b'

Under these constraints, preference between A and -A can change as P(C) = c moves out to either end of the unit interval in thought-experiments addressing the question "What would des A - des -A be if I found I had the bad/good allele?" To carry out these experiments, note that we can write p = P(B | A) = P(AB)/P(A) =
 
 

 P(A | BC)P(B | C)P(C) + P(A | B-C)P(B|-C)P(-C)(1-c)
-----------------------------------------------------
             P(A | C)P(C) + P(A | -C)P(-C)

     abc +a' b' (1-c)           (1-a)bc + (1-a')b' (1-c)
p = ------------------    p' = --------------------------
       ac + a' (1-c)              (1-a)c + (1-a')(1-c)

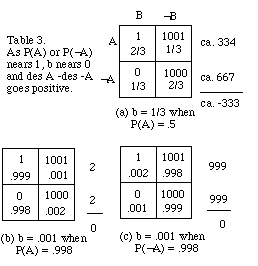
 The initial probabilities .093 and .025 in Table 1b were obtained by making the following substitutions in the formulas for p and p' above.
 
 

a = .9, a' = .5, b = .2, b' = .01, c (initially) = .3
 
 

As p and p' rise toward b = .2 or fall toward b' = .01, tracking the rise or fall of c toward 1 or 0, the negative difference des(continue) - des(quit) = -1.8 in Table 1b rises toward the positive values 5-4b = 4.2 and 5-4b' = 4.96 in Table 2. Unless you, the smoker, somehow becomes sure of your allele, neither of the two judgmental positions shown in Table 2 will be yours. The table only shows that for you, continuing is preferable to quitting in either state of certainty about the allele. The kinematical map leads you to that conclusion on any assumption about initial c. And initial uncertainty about the allele need not be modelled by a definite initial value of c. Instead, an indefinite initial probabilistic state can be modelled by the set of all pr assigning the values a, a' , b, b' as above, and with c = P(bad allele) anywhere in the unit interval.
 
 

If you are a smoker convinced of Fisher's hypothesis, your unconditional probabilities of continuing and quitting lag behind P(good) or P(bad) as your probability for the allele rises toward 1. In particular, your probability ac+a' (1-c) for continuing rises to a = .9 from its initial value of .62 or falls to a' = .5, as c rises to 1 from its initial value of .3 or falls to 0. Here you see yourself as committed by your genotype to one or the other of two mixed acts, analogs of gambles whose possible outcomes are pure acts of continuing and quitting, at odds of 9:1 or 1:1. You do not know which of these mixed acts you are committed to; your judgmental odds between them, c:(1-c), are labile, or perhaps undefined. This genetic commitment antedates your current deliberation. The mixed acts are not options for you; still less are their pure outcomes. (Talk about pure acts as options is shorthand for talk about mixed acts assigning those pure acts probabilities near 1.) Then there is much to be said for the judgment that quitting is preferable to continuing (sc., as the more desirable "news item"), for quitting and continuing are not options.
 
 

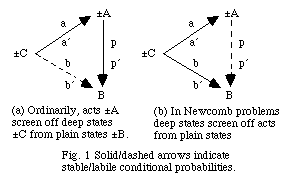
As a smoker who believes Fisher's hypothesis you are not so much trying to make your mind up as trying to discover how it is already made up. But this may be equally true in ordinary deliberation, where your question "What do I really want to do?" is often understood as a question about the sort of person you are, a question of which option you are already committed to, unknowingly. The diagnostic mark of Newcomb problems is a strange linkage of this question with the question of which state of nature is actual -- strange, because where in ordinary deliberation any linkage is due to an influence of acts +/- A on states +/- B, in Newcomb problems the linkage is due to an influence, from behind the scenes, of deep states +/- C on acts +/- A and plain states +/- B. This difference explains why deep states ("the sort of person I am") can be ignored in ordinary decision problems, where the direct effect of such states is wholly on acts, which mediate any further effect on plain states. But in Newcomb problems deep states must be considered explicitly, for they directly affect plain states as well as acts (Fig. 1).

 In the kinematics of decision the dynamical role of forces can be played by acts or deep states, depending on which of these is thought to influence plain states directly. Ordinary decision problems are modelled kinematically by applying the rigidity condition to acts as causes. Ordinarily, acts screen off deep states from plain ones in the sense that B is conditionally independent of +/- C given +/- A, so that while it is variation in c that makes P(A) and P(B) vary, the whole of the latter variation is accounted for by the former (Fig. 1a). But to model Newcomb problems kinematically we apply the rigidity condition to the deep states, which screen off acts from plain states (Fig. 1b). In Fig. 1a, the probabilities b and b' vary with c in ways determined by the stable a's and p's, while in Fig. 1b the stable a's and b's shape the labile p's as we have seen above:
 
 

     abc +a' b' (1-c)           (1-a)bc + (1-a')b'(1-c)
p = ------------------    p' = --------------------------
       ac + a' (1-c)              (1-a)c + (1-a')(1-c)

     apc +a' p' (1-c)           (1-a)pc + (1-a')p'(1-c)
b = ------------------    b' = --------------------------
       ac + a' (1-c)              (1-a)c + (1-a')(1-c)

P(B | act & C) = P(B | C), P(B | act & -C) = P(B | -C)
 
 

As Leeds (1984) points out in another connection, no purpose would be served by packing such announcements into the hypotheses themselves, for at best -- i.e., if true -- such announcements would be redundant. The causal talk, however useful as commentary, does no work in the matter commented upon.
 

4.5 Newcomb

Suppose a being in whose power to predict your choices you have enormous confidence. (One might tell a science-fiction story about a being from another planet, with an advanced technology and science, who you know to be friendly, and so on.) You know that this being has often correctly predicted your choices in the past (and has never, so far as you know, made an incorrect prediction about your choices), and furthermore you know that this being has often correctly predicted the choices of other people, many of whom are similar to you, in the particular situation to be described below. One might tell a longer story, but all this leads you to believe that almost certainly this being's prediction about your choice in the situation to be discussed will be correct.

... The being has surely put $1,000 in one box, and (B) left the second empty or (-B) put $1,000,000 in it, depending on whether the being predicts that you will take (A) both boxes, or (-A) only the second.

 Here you are to imagine yourself in a probabilistic frame of mind where your desirability for -A is greater than that of A because although you think A's truth or falsity has no influence on B's, your 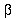 is near 1 (sec. 4.3), i.e., p is near 1, p' near 0. Does that seem a tall order? Not to worry! High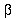 is a red herring; a tiny bit will do, e.g., if desirabilities are proportional to dollar payoffs, then the 1-box option, -A, maximizes desirability as long as 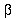 is greater than .001.

 To see how that might go, think of the choice and the prediction as determined by independent drawings by the agent and the predictor from the same urn, which contains tickets marked "2" and "1" in an unknown proportion x : 1-x. Initially, the agent's unit of probability density over the range [0,1] of possible values of x is flat (Fig. 2a), but in time it can push toward one end of the unit interval or the other, e.g., as in Fig. 2b, c. At t = 997 these densities determine the probabilities and desirabilities in Table 3b and c, and higher values of t will make des A - des -A positive. Then if t is calibrated in thousandths of a minute this map has the agent preferring the 2-box option after a minute's deliberation. The urn model leaves the deep state mysterious, but clearly specifies its mysterious impact on acts and plain states.

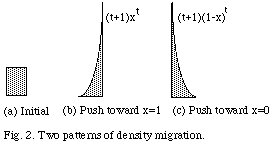
The irrelevant detail of high 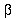 was a bogus shortcut to the 1-box conclusion, obtained if  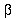is not just high but maximum, which happens when p = 1 and p' = 0. This means that the "best" and "worst" cells in the payoff table have unconditional probability 0. Then taking both boxes means a thousand, taking just one means a million, and preference between acts is clear, as long asthe probability r of A (take both boxes), is neither 0 nor 1, and 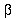 remains maximum, 1. The density functions of Fig. 2 are replaced by probability assignments r and 1-r to the possibilities that the ratio of 2-box tickets to 1-box tickets in the urn is 1:0 and 0:1, i.e., to the two ways in which the urn can control the choice and the prediction deterministically and in the same way. In place of the smooth density spreads in Fig. 2 we now have point-masses r and 1-r at the two ends of the unit interval, with desirabilities of the two acts constant as long as r is neither 0 nor 1. Now the 1-box option is preferable throughout deliberation, up to the very moment of decision. But of course this reasoning uses the premise that 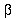 =1 through deliberation, a premise making abstract sense in terms of uniformly stocked urns, but very hard to swallow as a real possibility.
 
 
 

4.6 Hofstadter

Hofstadter (1983) saw prisoners's dilemmas as down-to-earth Newcomb problems. Call the prisoners Alma and Boris. If one confesses and the other does not, the confessor goes free and the other serves a long prison term. If neither confesses, both serve short terms. If both confess, both serve intermediate terms. From Alma's point of view, Boris's possible actions (B, confess, or -B, don't) are states of nature. She thinks they think alike, so that her choices (A, confess, -A, don't) are pretty good predictors of his, even though neither's choices influence the other's. If both care only to minimize their own prison terms this problem fits the format of Table 1(a). The prisoners are thought to share a characteristic determining their separate probabilities of confessing in the same way -- independently, on each hypothesis about that characteristic. Hofstadter takes that characteristic to be rationality, and compares the prisoners's dilemma to the problem Alma and Boris might have faced as bright children, independently working the same arithmetic problem, whose knowledge of each other's competence and ambition gives them good reason to expect their answers to agree before either knows the answer: "If reasoning guides me to [... ], then, since I am no different from anyone else as far as rational thinking is concerned, it will guide everyone to [... ]." The deep states seem less mysterious here than in the flagship Newcomb problem; here they have some such form as C_x" = We are both likely to get the right answer, i.e., x. (And here ratios of utilities are generally taken to be on the order of 10:1 instead of the 1000:1 ratios that made the other endgame so demanding. With utilities 0, 1, 10, 11 instead of 0, 1, 1000, 1001, indifference between confessing and remaining silent now comes at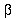  = 10% instead of one tenth of 1%.) But to heighten similarity to the prisoners's dilemma let us suppose the required answer is the parity of x, so that the deep states are simply C = We are both likely to get the right answer, i.e., even, and -C = We are both likely to get the right answer, i.e., odd.

 What's wrong with Hofstadter's view of this as justifying the coö perative solution? [And with von Neumann and Morgenstern's (p. 148) transcendental argument, remarked upon by Skyrms (1990, pp. 13-14), for expecting rational players to reach a Nash equilibrium?] The answer is failure of the rigidity conditions for acts, i.e., variability of P(He gets x | I get x) with P(I get x) in the decision maker's kinematical map. It is Alma's conditional probability functions P(-- | +/- C) rather than P(-- | +/- A) that remain constant as her probabilities for the conditions vary. The implausibility of initial des(act) as a figure of merit for her act is simply the implausibility of positing constancy of 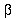 as her probability function p_r evolves in response to changes in P(A). But the point is not that confessing is the preferable act, as causal decision theory would have it. It is rather that Alma's problem is not indecision about which act to choose, but ignorance of which allele is moving her.
 
 
 

4.7 Conclusion

 The story was meant to be a credible, down-to-earth Newcomb problem; after all, Fisher (1959) honestly did give his hypothesis some credit. But if your genotype commits you to one mixed act or the other, to objective odds of 9:1 or 1:1 on continuing, there is no decision left for you to make. Yet, the story persuaded us that, given your acceptance of the Fisher hypothesis, you would be foolish to quit, or to try to quit: continuing would be the wiser move. This is not to say you will surely continue to smoke, i.e., not to say you see a mixed act at odds of 1:0 on continuing as an option, and, in fact, as the option you will choose. It only means you prefer continuing as the pure outcome of whichever mixed act you are unknowingly committed to. "Unknowingly" does not imply that you have no probabilistic judgment about the matter -- although, indeed, you may have none, i.e., c may be undefined. In fact, with c = .3, you think it unlikely that your commitment makes odds of 9:1 on continuing; you think the odds most likely to be 1:1 But whatever the odds, you prefer the same pure outcome: continuing. You don't know which "gamble" you face, but you know what constitutes winning: continuing to smoke, i.e., the less likely outcome of the more desirable "gamble." These scare-quotes emphasize that your mixed act is not a matter of spinning a wheel of fortune and passively awaiting the outcome; you yourself are the chance mechanism.

 You think there is an objective, real probability of your quitting, i.e., .9 or .5, depending on whether you have the bad genotype or the good one; there is a fact of the matter, you think, even though you do not know the fact. If the real odds on your continuing to smoke are even, that is because your tropism toward smoking is of the softer kind, stemming from the good allele; you are lucky in your genotype. But how does that work? How does the patch of DNA make you as likely to quit as continue? How do we close the explanatory gap from biochemistry to preference and behavior, i.e., to things like the relative importance you place on different concomitants of smoking, on the positive side a certain stimulus and sensual gratification, on the negative a certain inconvenience and social pressure? These influences play themselves out in the micro-moves which add up to the actual macro-outcome: continue, or quit. And if the odds are 9:1, that will stem from a different pattern of interests and sensitivities, forming a strong tropism toward continuing to smoke, somehow or other rooted in your DNA. What's weird about Fisher's science fiction story is not its premise, that the mental and physical states of reasoning animals are interconnected, but the thought that we might have the sort of information about the connection that his story posits -- information unneeded in ordinary deliberation, where acts screen it off.

 The flagship Newcomb problem owes its bizarrerie to the straightforward character of the pure acts: surely you can reach out and take both boxes, or just the opaque box, as you choose. Then as the pure acts are options, you cannot be committed to either of the non-optional mixed acts. But in the Fisher problem, those of us who have repeatedly "quit" easily appreciate the smoker's dilemma as humdrum entrapment in some mixed act, willy nilly. That the details of the entrapment are describable as cycles of temptation, resolution and betrayal makes the history no less believable -- only more petty. Quitting and continuing are not options, i.e., p_r A ~ 0 and p_r A ~ 1 are are not destinations you think you can choose, given your present position on your kinematical map, although you may eventually find yourself at one of them. The reason is your conviction that if you knew your genotype, your value of p_r A would be either a or a' , neither of which is ~ 0 or ~ 1. (Translation: "At places on the map where p_r C is at or near 0 or 1, p_r A is not.") The extreme version of the story, with a ~ 1 and a' ~ 0, is more like the flagship Newcomb problem; here you do see yourself as already committed to one of the pure acts, and when you learn which that is, you will know your genotype.

 I have argued that Newcomb problems are like Escher's famous staircase on which an unbroken ascent takes you back where you started. We know there can be no such things, but see no local flaw; each step makes sense, but there is no way to make sense of the whole picture; that's the art of it.
 
 
 

4.8 Notes

 (Sec. 4.2) Rigidity is also known as "sufficiency" (Diaconis and Zabell). A sufficient statistic is a random variable whose sets of constancy ("data") form a partition satisfying the "rigidity" condition.

²(Sec. 4.3, 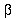 ) The "regression coefficient" of a random variable Y on another, X, is 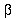 = cov(X,Y)/var(X), where cov(X,Y) = E[(X-EX)(Y-EY)] and var(X) = E(X-EX)². If X and Y are indicators of propositions (sc., "cause" and "effect"),

 cov(X,Y) = P(cause & effect)-P(cause)P(effect),

 var(X) = P(cause)P(-cause),

 and 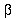 reduces to the left-hand side of the inequality.

³(Sec. 4.3, rigidity) For random variables generally, rigidity is constancy of the conditional probability distribution of Y given X as the unconditional probability distribution of X varies.

⁴(Sec. 4.4) In the example, I take it that the numerical values a = .9, a' = .5, b = .2, , b' = .01 hold even when c is 0 or 1, e.g. b = P(ca | bad) = .2 even when P(bad) = 0; the equation b. P(bad) = P(ca & bad) isn't what defines b.

⁵(Sec. 4.5, Fig. 2) In this kinematical map, P(A) = 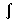 ₀¹x^t+1f(x)dx and P(B | A) = 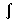 ₀¹x^t+2f(x)dx/P(A), with f(x) as in Fig. 2(b) or (c). Thus, with f(x) as in (b), P(A) = (t+1)/(t+3) and P(B | A) = (t+2)/(t+3). See Jeffrey (1988).

⁶(Sec. 4.5, end) At the moment of decision the desirabilities of shaded rows in (b) and (c) are not determined by ratios of unconditional probabilities, but continuity considerations suggest that they remain good and bad, respectively.

⁷(Sec. 4.7, start of third paragraph) "You think there is an objective, real probability... " See the hard-core subjectivist's guide to objective chance in The Logic of Decision, sec. 12, and note that the "no one chooses to have sacked Troy" passage from the Nichomachean Ethics, used by Skyrms (1980, p. 128) to introduce causal decision theory, also fits the present skepticism about Newcomb problems.

 (Sec. 4.7, end of third paragraph) Cf. Davidson's conclusion, that "nomological slack between the mental and the physical is essential as long as we conceive of man as a rational animal" ( p. 223).

 (Sec. 4.7, Escher staircase) "Ascending and Descending" (lithograph, 1960), based on Penrose (1958); see Escher (1989, p. 78). Elsewhere I have accepted Newcomb problems as decision problems, and accepted "2-box" solutions as correct. Jeffrey (1983, sec. 1.7 and 1.8) proposed a new criterion for acceptability of an act -- "ratifiability" -- which proved to break down in certain cases (see Jeffrey 1990, p. 20). In Jeffrey (1988, 1993), ratifiability was recast in terms more like the present ones -- but still treating Newcomb problems as decision problems.
 
 
 

4.9 References

 Bolker, E. (1965), Functions Resembling Quotients of Measures, Ph. D. dissertation (Harvard University).

 ------ (1966),`Functions resembling quotients of measures', Transactions of the American Mathematical Society, vol. 124, pp. 292-312.

 ------ (1967), "A simultaneous axiomatization of utility and subjective probability', Philosophy of Science, vol. 34, pp. 333-340.

 Davidson, D. (1980), Essays on Actions and Events (Oxford: Clarendon Press).

 Diaconis, P. and Zabell, S. (1982), `Updating subjective probability'. Journal of the American Statistical Asociation, vol. 77, pp. 822-830.

 Escher, M.C. (1989), Escher on Escher (New York: Abrams).

 Fisher, R. (1959), Smoking, the Cancer Controversy (London: Oliver and Boyd).

 Hofstadter, D.R. (1983), `The calculus of coö peration is tested through a lottery', Scientific American, vol. 248, pp. 14-28.

 Jeffrey, R.C. (1965; 1983, 1990) The Logic of Decision (New York: McGraw-Hill; Chicago: University of Chicago Press).

 ------ (1987), `Risk and human rationality' The Monist, vol. 70, no. 2, pp. 223-236.

 ------ (1988), `How to probabilize a Newcomb problem', Fetzer, J.H. (ed.), Probability and Causality (Dordrecht: Reidel).

 ------ (1992), Probability and the Art of Judgment, Cambridge.

 ------ (1993), `Probability kinematics and causality', in Hill, D., Forbes, M. and Okruhlik, K. (eds.) PSA 92, vol. 2 (Philosophy of Science Assn.: Michigan State University, E. Lansing, MI).

 Kolmogorov, A.N. (1933),`Grundbegriffe der Wahrscheinlichkeitsrechnung', Ergebnisse der Mathematik, Vol. 2, No. 3; Springer, Berlin. Translation: Foundations of Probability (New York: Chelsea, 1950).

 Leeds, S. (1984), `Chance, realism, quantum mechanics', Journal of Philosophy, vol. 81, pp. 567-578.

 Nozick, R. (1963) The Normative Theory of Individual Choice, Ph. D. dissertation (Princeton University).

 ------ (1969), `Newcomb's problem and two principles of choice', in N. Rescher (ed.), Essays in Honor of Carl G. Hempel, (Dordrecht: Reidel).

 ------ (1990) Photocopy of Nozick (1963), with new preface (New York: Garland).

 Penrose, L.S. and Penrose, R (1958), `Impossible Objects: a Special Type of Visual Illusion', The British Journal of Psychology, vol. 49, pp. 31-33.

 Skyrms, B. (1980) Causal Necessity (New Haven: Yale).

 ------ (1990), The Dynamics of Rational Deliberation (Cambridge, Mass: Harvard).

 von Neumann, J and Morgenstern, O. (1943, 1947), Theory of Games and Economic Behavior (Princeton: Princeton University Press).