Introduction

The old problem is thereby postponed, not solved. As soon as the new problem is solved, the old one returns, as a request for the credentials of the solution: "What reason is there to expect the future/unobserved to resemble the past/observed with respect to such- and- such dichotomies or classificatory schemes or magnitudes?" The form of the question is further modified when we talk in terms of judgmental probability instead of all-or- none expectation of resemblance, but the new problem still waits, suitably modified.

It seems to me that Hume did not pose his problem before the means were at hand to solve it, in the probabilism that emerged in the second half of the seventeenth century, and that we know today primarily in the form that Bruno de Finetti gave it in the decade from 1928 to 1938. The solution presented here (to the old and new problems at once) is essentially present in Chapter 2 of de Finetti's 'La prevision' (1937), but he stops short of the last step, shifting in Chapter 3 to a different sort of solution, that uses the notion of exchangeability. At the end of this paper I shall compare and contrast the two solutions, and say why I think it is that de Finetti overlooked (or, anyway, silently balked at) the solution that lay ready to hand at the end of his Chapter 2.

5.1 Probabilism, what

( I ) est X = x_op_o + x_l p₁ + ^{. . .},

where the x_i are the different values that the magnitude X can assume, and each p_i is the probability that the value actually assumed is x_i (If X is a continuous magnitude, replace the sum by an integral.)

Estimation is not a matter of trying to guess the true value, e.g., 2.4 might be an eminenty reasonable estimate of the number of someone's children, but it would be a ridiculous guess. (If that was my estimate, my guess might be 2.) Similarly, taking the truth value of a proposition to be 1 or 0 depending on whether it is true or false, my estimate of the truth value of the proposition that I shall outlive the present century is about 1/2, which couldn't be the truth value of any proposition.

The probability you attribute to a proposition is your estimate of its truth value: if X is a proposition, then

(2) prob X = est X.

Here I follow de Finetti in taking propositions to be magnitudes that assume the value 1 at worlds where they are true, and 0 where false. This comes to the same thing as the more familiar identification of propositions with the sets of worlds at which they are true, and makes for smoothness here. Observe that (2) follows from (1), for as X can take only the two values 0 and 1, we can set x_o = 0 and x₁ = 1 in (1) to get

est X = 0p_o + 1p₁= p₁

where p_i is the probability that X assumes the value I, i.e., the probability (prob X) that X is true.

Still following de Finetti, I take estimation to be the basic concept, and define probability in terms of it. (The opposite tack, with estimation defined in terms of probability as in (1), is more familiar.) Then (2) is given the status of a definition, and the following axioms are adopted for the estimation operator.

(3) Additivity: est X + Y = est X + est Y

(4) Positivity: If X > 0 then est X > 0

(5) Normalization: est 1 = 1

(1 is the magnitude that assumes the value 1 everywhere. i.e., the necessary proposition. 'X > 0' means that X assumes negative values nowhere.)

Once understood, these axioms are as obvious as the laws of logic - - in token of which fact I shall call them and their consequences laws of 'probability logic' (de Finetti's 'logic of the probable'). Here they are, in English:

(3) An estimate of the sum of two magnitudes must be the sum of the two separate estimates.

(4) An estimate must not be negative if the magnitude estimated cannot be negative.

(5) If the magnitude is certainly I, the estimate must be 1 .

Additivity implies^l that for each real number k,

(6) est kX = k est X

The Kolmogorov axioms for probability are easy consequences of axioms (3)- (5) for estimation, together with (2) as a notational convention, i.e.,

(7) If X can take no values but 0 and I, then est X = prob X.

Here are the Kolmogorov axioms.

(8) Additivity: If XY= 0 then prob X + Y = prob X + prob Y

(9) Positivity: prob X>=0

(10) Normalization: prob 1 =1

(10) is just copied from the normalization axiom (5) for est. with 'est' transcribed as 'prob'. Positivity is the same for 'prob' as for 'est', given that when we write 'prob X' it goes without saying that X > 0, since a proposition X can assume no values but 0 and 1. And additivity of prob as above comes to the same thing as the more familiar version, i.e.,

If X and Y are incompatible propositions, prob X v Y = prob X + prob Y.

(With 0 for falsehood and 1 for truth, the condition XY = 0 that the product of X and Y be 0 everywhere comes to the same thing as logical incompatibility of X and Y; and under the condition XY = 0 the disjunction Xv Y, i.e., X + Y - XY in the present notation, comes to the same thing as the simple sum X + Y.)

A precise, complete opinion concerning a collection of propositions would be represented by a probability function defined on the truth functional closure of that collection. More generally, a precise, complete opinion concerning a collection of magnitudes might be represented by an estimation operator on the closure of that collection under the operations of addition and multiplication of magnitudes, and of multiplication of magnitudes by constants. (One might also include other options, e.g. closure under exponentiation, X^Y.)

Such are precise, complete opinions, according to probabilism. But for the most part our opinions run to imprecision and incompleteness. Such opinions can be represented by conditions on the variable 'est' or, equivalently, by the sets of particular estimation operators that satisfy those conditions Such sets will usually be convex, i.e., if the operators est_o and est₁ both belong to one, then so will the operator w_oest_o+w₁est₁, if the w's are non- negative real numbers that sum to 1. An example is given by what de Finetti (1970, 1974 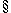3.10) calls 'The Fundamental theorem of probability':

Given a coherent assignment of probabilities to a finite number of propositions, the probability of any further propositions is either determined or can be coherently assigned any value in a certain closed interval.

Thus, the set of probability measures that assign the given values to the finite set of propositions must be convex. And incomplete, imprecise opinions can arise in other ways, e.g. in my book, The Logic of Decision (1965, 1983), a complete preference ranking will normally determine an infinite set of probability measures, so that probabilities of propositions may be determined only within intervals: see 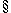6.6, 'Probability quantization'.

Probabilism would have you tune up your opinions with the aid of the probability calculus, or, more generally, the estimation calculus: probability logic, in fact. This is a matter of tracing consequences of conditions on estimation operators that correspond to your opinion. When you trace these consequences you may find that you had misidentified your opinion, i.e., you may see that after all, the conditions whose consequences you traced are not all such as you really accept. Note that where your opinion is incomplete or imprecise, there is no estimation operator you can call your own. Example: the condition est(X-- est X)² <= 1 is not a condition on your unknown estimation operator, est. Rather: in that condition, 'est' is a variable, in terms of which your opinion can be identified with the set { est: est (X est X)² <= 1 } of estimation operators that satisfy it.

5.2 Induction, what

              X1 + . . . + Xn       est X1 + . . . + est Xn
        est ------------------ = ---------------------------
                     n                         n

(11) An estimate of the average of any (finite) number of quantities must equal the average of the estimates of the separate quantities.

(Proof: use (6) to get 1/n out front, and then apply (3) n - 1 times.) From (11) we get what I shall call the

ESTIMATION THEOREM. If your opinion concerning the magnitudes X_l,...,X_n, .. ,X_n+m is characterized by the constraints est X_i = est X_j for all i, j = 1, ..., n + m (among other constraints, perhaps), then your estimate of the average of the last m of them will equal the observed average of the first n - if you know that average, or think you do.

Implicitly, this assumes that although you know that the average of the first n X's is (say) x, you don't know the individual values assumed by X_l,...,X_n separately unless it happens that they are all exactly x, for if you did, and they weren't, the constraint est X_i = est X_j would not characterize your opinion where the known value of X_i differs from the known value of X_j.

Proof of the estimation theorem. If you assign probability I to the hypothesis that the average of the first n X's is x, then by (1)² you must estimate that average as x The constraints then give est X_i = x for the last m X's, and the conclusion of the estimation theorem follows by (11).

Example 1: Guessing weight

For continuous magnitudes, estimates serve as guesses. Suppose that you will be rewarded if you guess someone's weight to within an accuracy of one pound. One way to proceed is to find someone who seems to you to be of the same build, to be dressed similarly, etc., so that where X₂ is the weight you wish to guess correctly, and X_l is the other person's weight, your opinion satisfies the constraint est X,=est X₂. Now have the other person step on an accurate scale, and use that value of X, as your estimate of X₂. This is an application of the estimation theorem with n = m = 1.

Mind you: it is satisfaction of the constraint after the weighing that justifies (or amounts to) taking the other person's actual weight as your estimate, and under some circumstances, your opinion might change as a result of the weighing so as to cease satisfying the constraint. Example: the other person's weight might prove to be so far from your expectation as to undermine your prior judgement that the two were relevantly similar, i.e., the basis for your prior opinion's satisfaction of the constraint. Here is a case where you had antecedently judged the two people both to have weights in a certain interval (say, from 155 to 175 pounds), so that when the other person's weight proved to be far outside this interval (perhaps, 120 pounds) your opinion changed from {est: 155 <= est X_l = est X₂< 175} to something else, because the weighing imposed the further condition est X_l = 120 on your opinion, i.e., a condition incompatible with the previously given ones. Probability logic need not tell you how to revise your opinion in such cases, any more than deductive logic need tell you which of an inconsistent set of premises to reject.

Example 2: Using averages as guesses

If you can find (say) ten people, each of whom strikes you as similar in the relevant respects to an eleventh person, whose weight you wish to guess, then have the ten assemble on a large platform scale, read their total weight, and use a tenth of that as your estimate of X_l1. This is an application of the estimation theorem with n = 10, m = 1. The estimation theorem does not endorse this estimate as more accurate than one based on a single person's weight, but under favorable conditions it may help you form an opinion of your estimate's accuracy, as follows.

Example 3: Variance

The variance of a magnitude X is defined relative to an estimation function:

var X = est (X - est X)² = est X² - est² X.

Thus, relative to an estimation function that characterizes your precise opinion, the variance of the eleventh person's weight is your estimate of the square of your error in estimating that weight, and this turns out to be equal to the amount by which the square of your estimate of the magnitude falls short of your estimate of the square of the magnitude. Now the estimation theorem can be applied to the magnitudes X_l², ..., X²_n+l to establish that under the constraints est X_i² = est Xj² for i, j = 1, ..., n + 1, your estimate of the square of the eleventh person's weight must equal the observed average of the squares of the first ten people's weights.³ To get the variance of X_l1, simply subtract from that figure the square of the estimate of X_l1 formed in Example 2.

It is worthwhile to ring the changes on these examples, e.g. imagining that you are estimating weights not by eye, but on the basis of significant but limited statistical data, say, age and sex of the members of the sample, and of the person whose weight is to be estimated; and imagining that it is not weight that is to be estimated, but length of life - the estimate of which has the familiar name, 'life expectancy'. (In this case the members of the sample are presumably dead already: people no younger than the one whose life expectancy is sought, who were relevantly similar to that one, at that age).

The estimation theorem was inspired by a class of applications (in 'La prevision', Chapter 2) of what I shall call

DE FINETTI'S LAW OF SMALL NUMBERS: your estimate of the number of truths among the propositions A1, ..., An must equal the sum of the probabilities you attribute to them .

Here is another formulation, obtained by dividing both sides of the equation by n and applying the linearity of est:

(12) Your estimate of the relative frequency of truths among the propositions A1,..., An must equal the average of the probabilities you attribute to them.

Proof of de Finetti's law. The claim is that est (A_l + ^{. . .} + A_n) = prob A_l + ^{. . .} + prob A_n, which is true by (3) and (7).

Example 4: Applying de Finetti's law

To form my probabilistic opinion concerning the proposition A_l01 that the 101st toss of a certain (possibly loaded) die will yield an ace, I count the number of times the ace turns up on the first hundred tosses. Say the number is 21, and suppose I don't keep track of the particular tosses that yielded the aces. It is to be expected that I attribute the same probability to all 101 propositions of form A_i, i.e., it is to be expected that my opinion satisfies the constraints est A_i = estA_j (i,j = 1, ...,101). Then by de Finetti's law with n = 100, the common value of those probabilities will be 21%, and that will be the probability of A_l01 as well.

Observe that in the case of propositions, i.e., magnitudes whose only possible values are 0 and 1, the variance is determined by the estimate, i.e., by the probability attributed to the proposition:

(13) If X is a proposition of probability p, then var X = p(l - p).

Proof. As X is a proposition, X² =X, and therefore var X, in the form est X^{2 -} est² X, can be written as est X - est² X, i.e., p - p², i.e., p(l - p). Thus, the variance of a proposition is null when its probability is extreme: 0, or 1. And variance is maximum (i.e., 1/4) when p is 1/2. You can see that intuitively by considering that the possible value of 'p' that is furthest from both of the possible values of X is the one squarely in the middle.

5.3 Justifying induction

Note that I say 'probability logic', not 'logical probability'. De Finetti's subjectivism implies that the basic axioms governing est (or, if you prefer, the corresponding axioms for prob) are all the universally valid principles there are, for this logic. In contrast, Carnap (1950,1952, 1971, 1980) tentatively proposed further principles as universal validities for what he called 'logical probability', i.e., either a particular probability function, e.g. c* (1945, 1950), or a class of them, e.g. {c 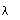: 0 < 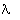< 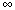} (1952). But such attempts to identify a special class of one or more probability functions as the 'logical' ones strike me as hopeless. Example: the functions of form c 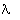. do have interesting properties that recommend them for use as subjective probability functions in certain sorts of cases, but there are plenty of other sorts of cases where none of those functions are suitable.⁴ Carnap (1980, 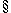17) did see that, and finally added further adjustable parameters and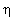, in an effort to achieve full generality. But I see no reason to think that would have been the end of the broadening process, had Carnap lived to continue it, or had others taken sufficient interest in the project to pursue it after Carnap's death⁵. With de Finetti, I take the laws of probability logic to be the axioms (3)-(5) and their consequences⁶.

It seems appropriate to call these axioms 'logical' because of the strength and quality of their grip, as constraints that strike us as appropriate for estimation functions. The feel of that grip is like that of the grip of such logical laws (i.e., constraints on truth- value assignments) as that any proposition, X, implies its disjunction with any proposition, Y. In our notation, this comes out as X <= X + Y - XY, given that X and Y take no values other than 0 and 1. I am at a loss to think of more fundamental principles from which to deduce these axioms: to understand is to acknowledge, given what we understand by 'estimate.'

But this is not to deny that illustrations can serve to highlight this logical character of the axioms: a notable class of such illustrations are the 'Dutch book' arguments, which proceed by considering situations in which your estimates of magnitudes will be the prices- in dollars at which you are constrained to buy or sell (on demand) tickets that can be exchanged for numbers of dollars equal to the true values of those magnitudes

Example. The Dutch book argument for axiom (3) goes like this, where x and y are the unknown true values of the magnitudes X and Y. For definiteness, we consider the case where the axiom fails because the left- hand side is the greater. (If it fails because the left- hand side is the smaller, simply interchange 'buy' and 'sell' in the following argument, to show that you are willing to suffer a sure loss of est X + est Y est (X + Y).)

If est (X + Y) exceeds est X + est Y, you are willing to buy for est (X + Y) dollars a ticket worth x +y dollars; and for a lower price, i.e., est X + est Y dollars, you are willing to sell a pair of tickets of that same combined worth: x +y dollars. Thus, you are willing to suffer a sure loss, viz., est (X + Y) - est X - est Y dollars.

To paraphrase Brian Skyrms (1980, p. 119): if your estimates violate axiom (3) in such cases, you are prepared to pay different amounts for the same good, depending on how it is described. For a single ticket worth x + y dollars you will pay est (X + Y) dollars, but for two tickets jointly worth x + y dollars you will pay a different amount, i.e., est X + est Y dollars. In a certain clear sense, this is an inconsistency.

Such Dutch book arguments serve to highlight the credentials of (3) (5) as axioms of the logic of estimation, i.e., of probability logic. One might even think of them as demonstrating the apriori credentials of the axioms, sc., as 'logical' truths in a certain sense under the hypothesis that you are prepared to make definite estimates of all the magnitudes that appear in them, in circumstances where those estimates will be used as your buying- or- selling prices for tickets whose dollar values equal the true values of those magnitudes. But the point of such demonstrations is blunted if one's opinions are thought to be sets of estimation functions, or conditions on estimation functions, for then the hypothesis that you are prepared to make the definite estimates that the Dutch book arguments relate to will be satisfied only in the extreme cases where opinion is precise and complete, relative to the magnitudes in question.

5.4 Solution or evasion?

Even if you see the Dutch book arguments as only suggestive, not demonstrative, you are unlikely to balk at the logicist solution to the old problem of induction (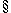 3) if you accept the probabilistic solution floated in 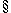2 for the new problem. But many will see probabilism as an evasion, not a solution; and while there can be no perfectly decisive answer to such doubts, it would be evasive to end this paper without some effort to meet them.

The doubt can be illustrated well enough in connection with Example 1: "Indeed, if you maintain your initial opinion, according to which your estimates of the two people's weights will be the same, the information that one of them weighs (say) 132 pounds will produce a new opinion in which both weights are estimated as 132 pounds. But to use your initial opinion as a datum in this way is to beg the question ("What shall your opinion be?") that the new problem poses. It is only by begging that question that the old problem can be misconceived as a request for the credentials of the general constraints (3) (5) on all estimation functions, rather than for the special constraints that characterize your own opinion."

That's the question which a probabilist must fault as question- begging in a characteristically objectivistic way. For that question contrasts your initial opinion, according to which est X₁, = est X₂, with the information that the true value of X₁, is 132. But what is thus dignified as 'information' is more cautiously described as a new feature of your opinion, specified by two new constraints:

estX₁ = 132, varX₁ = 0

It is the second of these that corresponds to the objectivistic characterization of the new estimate, 132, as information, not mere opinion. To interpret 'information' more strongly than this is to beg the question that the agent answers (in effect) by forming his new opinion in accordance with the new constraints: it is to say that his opinion about X, is not only definite (estX₁ = 132) and confident (varX₁ = 0) but correct.

In turn, objectivists will identify this move as a typical subjectivistic refusal to see the difference between subjective confidence and objective warrant. "If the only constraints that my opinion must meet are the basic axioms, I am free to adopt any further constraints I please, as long as they are consistent. But then I don't need to go through the business of finding somebody who strikes me as similar in build, weight of clothing, etc., to the person whose weight I wish to guess, and weighing that similar person. I can simply decide on any number at all (it might even be 132, as luck would have it), and use that as my guess: est X₂ = 132. Nor does anything prevent me from adopting great confidence regarding that guess: var X₂=0". (Note that in Example 1, where var X₁ was 0, there was no reason to set var X₂ = 0 as well.)

But this is nonsense, on a par with "If God is dead then everything is permitted". Look at it for a minute: God didn't die, either suddenly or after a long illness. The hypothesis is rather that there is no such entity, and never was. Our morality has no divine basis. Instead, its basis is in us: it is as it is because and insofar as we are as we are. ('Insofar as': humans are not as uniform as the divine template story suggests.) Moses smuggled the ten commandments up Mt. Sinai, in his heart. You know the line.

I take the same line about Carnap's efforts, and Henry Kyburg's, to tell us just what constraints on our probabilistic opinions would be rationally justified by this or that corpus of fully- held beliefs. If you think that some such set of epistemological commandments must be produced and justified if we are to form warranted probabilistic opinions, then you will find subjectivistic probabilism offensively nihilistic: a license for wishful thinking and all other sorts of epistemological sin. But I think such fears unwarranted. Wishful thinking is more commonly a feature of (shared or private) fantasy than of judgement. In forming opinion we aim to the truth, for the most part. The fact that I would be violating no laws of logic if I were simply to decide on a number out of the blue, as my estimate of someone's weight, does not mean that I would or could do that. (I could say '132' or '212' easily enough, but could I believe it?)

In a way, the contrast with von Mises' frequentism is more illuminating than that with Carnap's logicism. Mises sought to establish probability theory as an independent science, with its own subject- matter: mass phenomena. If that were right, there would be a general expertise for determining probabilities of all sorts: concerning horse races, the weather, U₂₃₅--whatever. But according to the sort of probabilism I am putting forward, such expertise is topical: you go to different people for your opinions about horse races, weather, U₂₃₅ etc. Probability logic provides a common framework within which all manner of opinion can be formulated, and tuned.

In the weight- guessing example you are supposed to have sought, and found, a person you saw as sufficiently similar in relevant respects to the one whose weight you wished to estimate, to persuade you that within broad limits, any estimate you form for the one (e.g. by weighing him on a scale you trust) will be your estimate for the other as well. Objectivism is willing to accept your judgement that the true value of X₁, is 132, based on the scale reading, but rejects the part of your judgement that identifies the two estimates. But probabilism views both scale- reading and equality-judging (for people's weights) as acquired skills. (The same goes for judging the accuracy of scales.) The point about scale- reading is that it is a more widely and uniformly acquired skill, than is equality-judgement for people's weights. But when it comes down to it, your opinion reflects your own assessment of your own skills of those sorts.

Here is how de Finetti (1938) expressed the basic attitude:

...one must invert the roles of inductive reasoning and probability theory: it is the latter that has autonomous validity, whereas induction is the derived notion. One is thus led to conclude with Poincare that "whenever we reason by induction we make more or less conscious use of the calculus of probabilities".

The difference between the approach to the problem of induction that I suggest here and the one de Finetti espoused in 'La prévision...' is a consequence of the difference between de Finetti's drive to express uncertainty by means of definite probability or estimation functions (e.g. 'exchangeable' ones (1937) and 'partially exchangeable' ones (1938)), and the looser course taken here, where opinions can be represented by constraints on estimation functions in cases where no one function adequately represents the opinion. By taking this looser point of view,' one can use the mathematically trivial estimation theorem to find that under the constraints est X₁ = ^{. . .} = est X_n+m, observed averages must be used as estimates of future averages, on pain of incoherence, i.e., inconsistency with the canons of probability logic. In contrast, de Finetti (1937) uses the mathematically nontrivial law of large numbers, according to which one's degree of belief in the difference between any two averages' exceeding (say) 10^-10 can be made as small as you like by making the numbers of magnitudes X_i that appear in the averages both get large enough. The constraint in de Finetti's version of the law of large numbers are stronger than those in the estimation theorem: they require existence of real numbers a, b, c for which we have

estX_i = a, est X_i² = b, est(X_iX_j) = c

for all i, j = 1,2, ... with i != j. (Only the first of these constraints applies to the estimation theorem, and then only for i = 1, ...,n + m.)

I think that de Finetti spurns or overlooks the estimation theorem because he insists on representing opinions by definite probability and estimation functions. He then uses conditionalization to take experience into account. As the presumed initial opinion is precise and complete, he gets not only precise estimates of averages in this way, but precise variances, too . It is a merit of the estimation theorem that it uses a very diffuse initial opinion, i.e., one that need satisfy no constraints but est X₁ = ^{. . .} = est X_n+m . There is no use of conditionalization in proving or applying the estimation theorem. If variances are forthcoming, it is by a further application of the estimation theorem, as in Example 3: empirically, in large part⁸.

The claim is that through the estimation theorem, probabilism makes what considerable sense there is to be made of naive frequentism⁹, i.e., of Hume's inductivism in its statistical atavar.

Notes

2 (1) is deducible from (3), (6), and (7) in case X assumes only finitely many different values x_i, for then we have X= vixSXs where X_i is the proposition that X = x_i, i.e., X_i assumes the value 1 (0) at worlds where X is true (false).

3 The constraints est X_i2 = est X_j2 represent a judgement quite different from that represented by the constraints est X_i = est X_j a judgement we are less apt to make, or to feel confident of, having made it. (Note that estimating x ₂ is not generally just a matter of squaring your estimate of X!)

4 As Johnson (1932) showed, and Kemeny (1963) rediscovered, the cases where one of the functions cx is suitable are precisely those in which the user takes the appropriate degree of belief in the next item's belonging to cell P_i Of the partitioning {P₁, ...,P_k} to depend only on (i) the number of items already sorted into cells of that partitioning, and (ii) the number among them that have been assigned to cell P_i.

5 Not everyone would agree that nobody is continuing work on Carnap's project, e.g. Costantini (1982) sees himself as doing that. But as I see it, his program - a very interesting one - is very different from Carnap's.

6 There are two more axioms, which de Finetti does not acknowledge: an axiom of continuity, and an axiom that Lewis (1980) calls 'The Principal Principle' and others call by other names: prob (H 1 chance H = x ) = x, where chance H is the objective chance of H's truth. De Finetti also omits axiom (5), presumably on the ground that the estimates of magnitudes are to represent estimates of the utilities you expect from them, where the estimated utility est X need not be measured in the same units as X itself, e.g. where X is income in florins, est X might be measured in dollars.

7 I gather that it originates with Keynes (1921), reappears with Koopman (1940), and is given essentially the form used here by Good (1950, e.g. p. 3). It is espoused by Levi (1974,1980) as part of a rationalistic program. I first encountered it, or something like it, in Kyburg (1961), but it took me 20 years to see its merits. Among statisticians, the main support for this way of representing imprecise or incomplete opinion comes from Good (1950, 1962), Smith (1961), Dempster (1967, 1968), and Shafer (1976). In practice, the business of reasoning in terms of a variable, prob' or 'est', that satisfies certain constraints, is widespread - but with an unsatisfactory rationale, according to which one is reasoning about an unknown, definite function, which the variable denotes.

8 Anyway, in larger part than in de Finetti's approach. Use of the observed average is common to both, but the further constraints on est are weaker in this approach than in de Finetti's. Observe that with the symmetric flat prior probability function (Carnap's C#), conditioning on the proposition that m of the first n trials have been successes yields a posterior probability function prob relative to which we always have prob X₁ = ^{. . .} = prob X_n = m/n, but have prob X_n+1 = (m + 1)/(n + 2) + m/n unless n = 2m. The case is similar for other nonextreme symmetric priors, e.g. for all of form

9 Not von Mises' science of limiting relative frequencies in irregular collectives, but the prior, plausible intuition.

References

Carnap, R.: 1945, 'On inductive logic', Philosophy of Science 12, 72 97.

Carnap, R.: 1950, Logical Foundations of Probability, Univ. of Chicago Press.

Carnap, R.: 1952, The Continuum of Inductive Methods, Univ. of Chicago Press.

Carnap, R.: 1971, 'A basic system of inductive logic', in Carnap and Jeffrey (eds.) (1971) and Jeffrey (ed.) (1980).

Carnap, R. and R. Jeffrey: 1971, Studies in Inductive Logic and Probability, Vol. 1, Univ. of California Press.

Costantini, D: 1982, 'The role of inductive logic in statistical inference', to appear in Proceedings of a Conference on the Foundations of Statistics and Probability, Luino, September 1981.

Dempster, Arthur P.: 1967, 'Upper and lower probabilities induced by a multivalued mapping', Annals of Mathematical Statistics 38, 395 339.

Dempster, Arthur P.: 1968, 'A generalization of Bayesian inference', J. Royal Stat. Soc., Series B. 30, 205 247.

Finetti, Bruno de: 1937, 'La prevision: ses lois logiques, ses sources subjectives', Annales de l'lnstitut Henri Poincare 7, 1- 68. (English translation in Kyburg and Smokler.)

Finetti, Bruno de: 1938, 'Sur la condition d'equivalence partielle', ActualEites Scient. et Industr., No. 739, Hermann & Cie., Paris. (English translation in Jeffrey (1980).)

Finetti, Bruno de: 1970, 1974, TeoHa Della Probabditai, Torino; English translation, Theory of Probability, Vol. 1, Wiley, New York. (Vol. 2, 1975).

Good, I. J.: 1950, Probability and the Weighing of Evidence, Griffin, London.

Good, I. J.: 1962, 'Probability as the measure of a non- measurable set', in Ernest Nagel, Patrick Suppes, and Alfred Tarski (eds.), Logic, Methodology, and Philosophy of Science: Proceedings of the 1960 International Congress, Stanford Univ. Press. Reprinted in Kyburg and Smokler.

Goodman, N.: 1979, Fact, Fiction and Forecast, Hackett Publ. Co., Indianapolis.

Hume, D.: 1739,A Treatise of Human Nature, London.

Jeffrey, Richard C.: 1965, 1983, The Logic of Decision, McGrawHill; 2nd ed., Univ of Chicago Press.

Jeffrey, Richard C.: 1980 (ed.), Studies in Inductive Logic and Probability, Vol. 2, Univ. of California Press.

Johnson, W. E.: 1932, 'Probability', Mind 41, 1- - 16, 281- 296, 408 423.

Kemeny, J: 1963, 'Carnap's theory of probability and induction', in P. A. Schilpp (ed.), The Philosophy of Rudolf Carnap, La Salle,111.

Keynes, John M.: 1921,A Treatise on Probabdity, London.

Kolmogorov, A. N.: 1933, Grundbegriffe der Wahrscheinlich-keitsrechnung, Ergebnisse der Msth., Band II, No. 3. (English Translation, Chelsea, N.Y., 1946.)

Koopman, B O.: 1940, 'The bases of probability', BuGetin of the American Mathematical Society 46, 763 774. Reprinted in Kyburg and Smokler.

Kyburg, Henry E., Jr.: 1961, Probability and the Logic of Rational Belief, Wesleyan Univ . Press, 1961.

Kyburg, Henry E., Jr. and Howard Smokler (eds.): 1980, Studies in Subjective Probability, 2nd ed., Krieger Publ. Co., Huntington, N.Y.

Levi, I.: 1974, 'On indeterminate probabilities', J. Phd. 71, 391418.

Levi, I.: 1980, The Enterprise of Knowledge, MIT Press.

Lewis, David K.: 1980, 'A subjectivist's guide to objective change', in Jeffrey (ed.) (1980).

Mises, Richard v.: 1919, 'Grundlagen der Wahrscheinhchkeitsrechnung', Math. Zs. 5.

Skyrms, B.: 'Higher order degrees of belief', in D. H. Mellor (ed.), Prospects for Pragmatism, Cambridge Univ. Press

Shafer, G.: 1976, A Mathematical Theory of Evidence, Princeton Univ. Press.

Smith, C. A. B.: 1961, 'Consistency in statistical inference and decision'. Royal Stat. Soc., Series B. 23,1 25.

Dept. of Philosophy

Princeton University

Princeton, N.J. 08544, U.S.A.