next up previous contents index
Next: Element Types Up: Format of the neutral Previous: Pre-defined FEMVIEW Calculations

Subsections

Examples

  The following examples illustrate the way in which data from a Finite Element Analysis should be formatted for input to FEMVIEW..

Model Geometry

  This example illustrates the way in which the geometry for a model may be defined using the nodal coordinates, and element topology data sets. The model shown below represents four flat plate elements (FEMVIEW element type 9) arranged in a square. 

    1CMODEL1
    2C
 -1    1 0.00000E+01 0.00000E+00 0.00000E+00
 -1    2 0.10000E+01 0.00000E+00 0.00000E+00
 -1    3 0.20000E+01 0.00000E+00 0.00000E+00
 -1    4 0.00000E+00 0.10000E+01 0.00000E+00
 -1    5 0.10000E+01 0.10000E+01 0.00000E+00
 -1    6 0.20000E+01 0.10000E+01 0.00000E+00
 -1    7 0.00000E+00 0.20000E+01 0.00000E+00
 -1    8 0.10000E+01 0.20000E+01 0.00000E+00
 -1    9 0.20000E+01 0.20000E+01 0.00000E+00
 -3
    3C
 -1    1    9    1    1
 -2    1    2    5    4
 -1    2    9    1    1
 -2    2    3    6    5
 -1    3    9    1    1
 -2    4    5    8    7
 -1    4    9    1    1
 -2    5    6    9    8
 -3
 9999

Note here that each of the elements has been assigned material 1 and group 1. It is permissible to leave these two fields blank if for example the material and group numbers are of no special interest. Material numbers will become necessary for materially dependant nodal results data sets, and group numbers are necessary in the element-wise results data sets because duplicate element numbers are allowed for elements in different groups. At run time the FEMVIEW commands `LABEL MESH MATERIALS', and `LABEL MESH GROUPS' may be used to highlight different elements if group and material numbers have been defined.

Nodal Attributes

 

Nodal Displacements

  This example illustrates the way in which nodal, materially independant results may be attributed to the model illustrated in the previous example. 

    1CMODEL2
    2C
 -1    1 0.00000E+01 0.00000E+00 0.00000E+00
 -1    2 0.10000E+01 0.00000E+00 0.00000E+00
 -1    3 0.20000E+01 0.00000E+00 0.00000E+00
 -1    4 0.00000E+00 0.10000E+01 0.00000E+00
 -1    5 0.10000E+01 0.10000E+01 0.00000E+00
 -1    6 0.20000E+01 0.10000E+01 0.00000E+00
 -1    7 0.00000E+00 0.20000E+01 0.00000E+00
 -1    8 0.10000E+01 0.20000E+01 0.00000E+00
 -1    9 0.20000E+01 0.20000E+01 0.00000E+00
 -3
    3C
 -1    1    9    1    1
 -2    1    2    5    4
 -1    2    9    1    1
 -2    2    3    6    5
 -1    3    9    1    1
 -2    4    5    8    7
 -1    4    9    1    1
 -2    5    6    9    8
 -3
  100CLCASE1 0.00000E+00            STATIC X LOAD NODE:7 0    0
 -4  DISPLACE    7    1    0
 -5  D-X         1    2    1    0    0
 -5  D-Y         1    2    2    0    0
 -5  D-Z         1    2    3    0    0
 -5  R-X         1    2    4    0    0
 -5  R-Y         1    2    5    0    0
 -5  R-Z         1    2    6    0    0
 -5  RESULTNT    1    2    0    0    1ALL
 -1    1 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00
 -1    2 0.10000E+00-0.50000E-01 0.00000E+00 0.00000E+00 0.00000E+00 0.11000E+00
 -1    3 0.15000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.12000E+00
 -1    4 0.10000E+00 0.50000E-01 0.00000E+00 0.00000E+00 0.00000E+00 0.11000E+00
 -1    5 0.20000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.16000E+00
 -1    6 0.20000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.15000E+00
 -1    7 0.30000E+00-0.50000E-01 0.00000E+00 0.00000E+00 0.00000E+00 0.14000E+00
 -1    8 0.30000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.14000E+00
 -1    9 0.10000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.12000E+00
 -3
 9999

Firstly note the results data set header; the step number and step value have been set to zero, and the calculation type set to static. The data set has been identified by the loadcase name `LCASE1' and some descriptive text has been included. This information serves to uniquely identify each results data set and is displayed by FEMVIEW when results from this data set are displayed.

The next record is the Attribute Header. Here it has been used to assign the name `DISPLACE' to this attribute with seven nodal materially independant components, and no Attribute Variants. The first six Component Definition Records have been assigned the names `D-X', `D-Y', `D-Z', `R-X', `R-Y', and `R-Z', representing three translations and three rotations.

For the translations, the numbers in the next three columns indicate that each component is to appear in the FEMVIEW menu, and is a cartesian X, Y, or Z vector component. For the rotations, the numbers in the next three columns indicate that each component is to appear in the FEMVIEW menu, and is a scalar rotation about the X, Y, or Z axis. The next column is not used for vector components and the last column indicates that each component exists as data in the results records. No pre-defined FEMVIEW calculations are needed to display these components so the remaining fields in each Component Definition Record are left blank.

The last component has been assigned the name `RESULTNT'. It too is a vector component to be included in the FEMVIEW results menu. The `1' in the last column indicates that this component is to be the result of a pre-defined FEMVIEW calculation. As such, the third and fourth columns are not used and have been set to zero. The string `ALL' indicates which pre-defined FEMVIEW calculation to use, and the blank field on the end of the record indicates that the source components for the calculation are in this data set. The component `RESULTNT' thus becomes the vector sum of the previous six components, and will be displayed as such by FEMVIEW..

Nodal Stress with Material Repeats

  This example illustrates the way in which nodal, materially dependant results may be attributed to the same model as above. In this example, the results are nodal stresses defined by a stress matrix. 

    1CMODEL3
    2C
 -1    1 0.00000E+01 0.00000E+00 0.00000E+00
 -1    2 0.10000E+01 0.00000E+00 0.00000E+00
 -1    3 0.20000E+01 0.00000E+00 0.00000E+00
 -1    4 0.00000E+00 0.10000E+01 0.00000E+00
 -1    5 0.10000E+01 0.10000E+01 0.00000E+00
 -1    6 0.20000E+01 0.10000E+01 0.00000E+00
 -1    7 0.00000E+00 0.20000E+01 0.00000E+00
 -1    8 0.10000E+01 0.20000E+01 0.00000E+00
 -1    9 0.20000E+01 0.20000E+01 0.00000E+00
 -3
    3C
 -1    1    9    1    1
 -2    1    2    5    4
 -1    2    9    1    2
 -2    2    3    6    5
 -1    3    9    1    1
 -2    4    5    8    7
 -1    4    9    1    2
 -2    5    6    9    8
 -3
  100CLCASE1 0.00000E+00            STATIC X LOAD NODE:7 0    0
 -4  STRESS      3    2    1
 -5  SXX         1    4    1    1    0
 -5  SYY         1    4    2    2    0
 -5  SXY         1    4    1    2    0
 -6    1    3  1  2  3
 -1    1    1    1    1
 -2    1 0.40000E+02 0.40000E+02 0.10000E+02
 -1    2    2    1    1
 -2    1 0.00000E+00 0.10000E+02 0.40000E+02
 -2    2 0.00000E+00 0.11000E+02 0.42000E+02
 -1    3    1    1    1
 -2    2 0.00000E+00 0.33000E+02 0.23000E+02
 -1    4    1    1    1
 -2    1 0.30000E+02 0.30000E+02 0.00000E+00
 -1    5    2    1    1
 -2    1 0.20000E+02 0.20000E+02 0.30000E+02
 -2    2 0.25000E+02 0.23000E+02 0.33000E+02
 -1    6    1    1    1
 -2    2 0.12000E+02 0.23000E+02 0.33000E+02
 -1    7    1    1    1
 -2    1 0.20000E+02 0.20000E+02 0.10000E+02
 -1    8    2    1    1
 -2    1 0.10000E+02 0.10000E+02 0.40000E+02
 -2    2 0.12000E+02 0.11000E+02 0.43000E+02
 -1    9    1    1    1
 -2    2 0.55000E+01 0.53000E+01 0.52000E+02
 -3
 9999

The Data Set Header Record is the same as in the previous example indicating that the same loadcase is being used. The Attribute Header Record which follows indicates that three components are present, and that they are nodal, materially dependant. One Attribute Variant Record is indicated.

The three stress components represent two direct stresses in the X and Y directions plus a Shear stress. Accordingly they have been allocated positions (1,1), (2,2) and (1,2) in the matrix definition above. These positions correspond to the standard definition of a stress tensor. When pre-defined FEMVIEW calculations are to be used on matrix components, only the components in the upper triangle of the matrix will be referenced.

An Attribute Variant Record has been included after the component definitions. In this particular case the example is trivial because the attribute variant record states that all components are present, and in the same order as in the component definitions.

This model has been changed from the previous example by defining two of the elements as being made of material 1, and the other two elements as material 2. There will be a stress discontinuity on the boundary between the materials. The nodes that lie on the boundary will thus have two sets of results, one for each material. This is reflected in the material repeats for the results records at nodes 2,5, and 8.

Nodal Stress for Multiple Surfaces and Materials

  This example illustrates the way in which nodal, materially dependant results may be formatted for multiple surfaces. The model is the same as in the previous example with different constraints and loading. 

  100CLCASE2 0.00000E+00            DISTRIBUTED -FZ LOAD 0    0
 -4  STRESS      3    2    0
 -5  SXX         1    4    1    1    0
 -5  SYY         1    4    2    2    0
 -5  SXY         1    4    1    2    0
 -1    1    1    3    0
 -2    1 0.80000E+02 0.00000E+00 0.70000E+02
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1-0.80000E+02 0.00000E+00-0.70000E+02
 -1    2    1    3    0
 -2    1 0.40000E+02 0.00000E+00 0.35000E+02
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1-0.40000E+02 0.00000E+00-0.35000E+02
 -1    3    1    3    0
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -1    4    2    3    0
 -2    1 0.80000E+02 0.00000E+00 0.70000E+02
 -2    2 0.83000E+02 0.00000E+00 0.73000E+02
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1-0.80000E+02 0.00000E+00-0.70000E+02
 -2    2-0.83000E+02 0.00000E+00-0.73000E+02
 -1    5    2    3    0
 -2    1 0.40000E+02 0.00000E+00 0.35000E+02
 -2    2 0.43000E+02 0.00000E+00 0.37000E+02
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1-0.40000E+02 0.00000E+00-0.35000E+02
 -2    2-0.43000E+02 0.00000E+00-0.37000E+02
 -1    6    2    3    0
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    1 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -1    7    1    3    0
 -2    2 0.83000E+02 0.00000E+00 0.73000E+02
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2-0.83000E+02 0.00000E+00-0.73000E+02
 -1    8    1    3    0
 -2    2 0.43000E+02 0.00000E+00 0.37000E+02
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2-0.43000E+02 0.00000E+00-0.37000E+02
 -1    9    1    3    0
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -2    2 0.00000E+00 0.00000E+00 0.00000E+00
 -3
 9999

The materials definitions have been changed to place the material boundary along nodes 4,5, and 6. The new loadcase simulates a cantilever arrangement with nodes 1,4, and 7 fixed, and a distributed -FZ load along the edge defined by nodes 3,6, and 9. This loading will generate a stress gradient through the thickness of the plates, and results will be presented at the top, middle, and bottom surfaces.

The attribute and component definitions remain the same as in the previous example. The Data Set Header Record has been changed to reflect the new loadcase. There are three repeats for most nodes reflecting the values at each of the three surfaces. Nodes 4,5, and 6 each have six sets of values because these nodes lie on the material boundary, generating a set of results for each material, at each surface. The number of materials serves as the inner repeat, and the number of surfaces as the outer repeat.

Elemental Attributes

 

Element-wise Results, Invariant

  This example uses the same model geometry as in previous examples. No loading or constraints have been assumed, and the results are in the form of a very simple temperature field. 

    1CMODEL5
    2C
 -1    1 0.00000E+01 0.00000E+00 0.00000E+00
 -1    2 0.10000E+01 0.00000E+00 0.00000E+00
 -1    3 0.20000E+01 0.00000E+00 0.00000E+00
 -1    4 0.00000E+00 0.10000E+01 0.00000E+00
 -1    5 0.10000E+01 0.10000E+01 0.00000E+00
 -1    6 0.20000E+01 0.10000E+01 0.00000E+00
 -1    7 0.00000E+00 0.20000E+01 0.00000E+00
 -1    8 0.10000E+01 0.20000E+01 0.00000E+00
 -1    9 0.20000E+01 0.20000E+01 0.00000E+00
 -3
    3C
 -1    1    9    1    1
 -2    1    2    5    4
 -1    2    9    1    1
 -2    2    3    6    5
 -1    3    9    1    1
 -2    4    5    8    7
 -1    4    9    1    1
 -2    5    6    9    8
 -3
  100CLCASE3 0.00000E+00            SIMPLE TEMP GRADIENT 0    0
 -4  TEMP        1    5    0
 -5              0    1    0    0    0
 -1    1    9    1    0
 -2    1 0.10000E+03
 -1    2    9    1    0
 -2    2 0.60000E+02
 -1    3    9    1    0
 -2    3 0.60000E+02
 -1    4    9    1    0
 -2    4 0.20000E+02
 -3
 9999

The Data Set Header Record has been changed to identify this new `loadcase'. The Attribute Header Record defines a single component, invariant over the element with no attribute variants. The single Component Definition Record defines an unamed component which is not to be included in the FEMVIEW menu, and is a scalar value. This component has not been included in the FEMVIEW menu because there is no need to select from a number of components in this example. Thus when using FEMVIEW the command `RESULTS INVARIANT TEMP' is sufficient to access the single component for this data set.

Element-wise Results at Element Nodes

  This example simulates the same loadcase as in example A.9.9.2.1 . Here, results have been presented for each element at the element nodes instead of being simply at model nodes. 

    1CMODEL6
    2C
 -1    1 0.00000E+01 0.00000E+00 0.00000E+00
 -1    2 0.10000E+01 0.00000E+00 0.00000E+00
 -1    3 0.20000E+01 0.00000E+00 0.00000E+00
 -1    4 0.00000E+00 0.10000E+01 0.00000E+00
 -1    5 0.10000E+01 0.10000E+01 0.00000E+00
 -1    6 0.20000E+01 0.10000E+01 0.00000E+00
 -1    7 0.00000E+00 0.20000E+01 0.00000E+00
 -1    8 0.10000E+01 0.20000E+01 0.00000E+00
 -1    9 0.20000E+01 0.20000E+01 0.00000E+00
 -3
    3C
 -1    1    9    1    1
 -2    1    2    5    4
 -1    2    9    1    1
 -2    2    3    6    5
 -1    3    9    1    1
 -2    4    5    8    7
 -1    4    9    1    1
 -2    5    6    9    8
 -3
  100CLCASE1 0.00000E+00            STATIC X LOAD NODE:7 0    0
 -4  STRESSEN    3    3    0
 -5  SXX         1    4    1    1    0
 -5  SYY         1    4    2    2    0
 -5  SXY         1    4    1    2    0
 -1    1    9    1    0    4    1
 -2    1 0.40000E+02 0.40000E+02 0.10000E+02
 -2    2 0.00000E+00 0.10000E+02 0.40000E+02
 -2    5 0.20000E+02 0.20000E+02 0.30000E+02
 -2    4 0.30000E+02 0.30000E+02 0.00000E+00
 -1    2    9    1    0    4    1
 -2    2 0.00000E+00 0.80000E+01 0.37000E+02
 -2    3 0.00000E+00 0.30000E+02 0.02000E+02
 -2    6 0.10000E+02 0.20000E+02 0.20000E+02
 -2    5 0.18000E+02 0.18000E+02 0.27000E+02
 -1    3    9    1    0    4    1
 -2    4 0.29000E+02 0.29000E+02 0.00000E+00
 -2    5 0.18000E+02 0.18000E+02 0.27000E+02
 -2    8 0.10000E+02 0.10000E+02 0.40000E+02
 -2    7 0.20000E+02 0.20000E+02 0.10000E+02
 -1    4    9    1    0    4    1
 -2    5 0.17000E+02 0.17000E+02 0.25000E+02
 -2    6 0.90000E+01 0.15000E+02 0.30000E+02
 -2    9 0.00000E+00 0.00000E+00 0.45000E+02
 -2    8 0.90000E+01 0.90000E+01 0.35000E+01
 -3
 9999

The elements in this example are four-noded flat plates. Thus up to four sets of results may be attributed to each element. Multi-surface results are possible for this type of results data set; in this case, the number of nodes serves as the inner repeat, and the number of surfaces the outer repeat, for each element.

Element-wise Results at Gauss Points

  This example illustrates the presentation of results at element gauss points. The cantilevered loadcase has been assumed, and the number of stress components has been reduced to a single SXX value for simplicity. It has been assumed that each element has four gauss points, although the actual number for this type of element will depend on the analysis package used. 

  100CLCASE2 0.00000E+00            DISTRIBUTED -FZ LOAD 0    0
 -4  STRESSGS    1    4    0
 -5  SXX         1    4    1    1    0
 -1    1    9    1    0    0    1    4
 -2    1 0.20000E+00 0.20000E+00 0.00000E+00
 -2    1 0.70000E+02
 -2    2 0.80000E+00 0.20000E+00 0.00000E+00
 -2    2 0.50000E+02
 -2    3 0.80000E+00 0.80000E+00 0.00000E+00
 -2    3 0.50000E+02
 -2    4 0.20000E+00 0.80000E+00 0.00000E+00
 -2    4 0.70000E+02
 -1    2    9    1    0    0    1    4
 -2    1 1.20000E+00 0.20000E+00 0.00000E+00
 -2    1 0.30000E+02
 -2    2 1.80000E+00 0.20000E+00 0.00000E+00
 -2    2 0.10000E+02
 -2    3 1.80000E+00 0.80000E+00 0.00000E+00
 -2    3 0.10000E+02
 -2    4 1.20000E+00 0.80000E+00 0.00000E+00
 -2    4 0.30000E+02
 -1    3    9    1    0    0    1    4
 -2    1 0.20000E+00 1.20000E+00 0.00000E+00
 -2    1 0.70000E+02
 -2    2 0.80000E+00 1.20000E+00 0.00000E+00
 -2    2 0.50000E+02
 -2    3 0.80000E+00 1.80000E+00 0.00000E+00
 -2    3 0.50000E+02
 -2    4 0.20000E+00 1.80000E+00 0.00000E+00
 -2    4 0.70000E+02
 -1    4    9    1    0    0    1    4
 -2    1 1.20000E+00 1.20000E+00 0.00000E+00
 -2    1 0.30000E+02
 -2    2 1.80000E+00 1.20000E+00 0.00000E+00
 -2    2 0.10000E+02
 -2    3 1.80000E+00 1.80000E+00 0.00000E+00
 -2    3 0.10000E+02
 -2    4 1.20000E+00 1.80000E+00 0.00000E+00
 -2    4 0.30000E+02
 -3
 9999

Each element has four Entity Data Records, one for each gauss point. Note that each data record is preceded by a gauss point coordinate record. Surface repeats are allowable for this type of data set, the number of gauss points serving as the inner repeat, and the number of surfaces as the outer repeat for each element. If surface repeats are included, a gauss point coordinate record must still be used for the same gauss point at different surfaces.

Transformations Data Sets

  This example illustrates the way in which Transformations Data Sets may be used to transform models. The example given illustrates how an eight-noded brick element may be shifted to different points in space using transformation data sets. 

    1CCUBE
    2C
 -1    1 0.00000E+00 0.00000E+00 0.00000E+00
 -1    2 1.00000E+00 0.00000E+00 0.00000E+00
 -1    3 1.00000E+00 1.00000E+00 0.00000E+00
 -1    4 0.00000E+00 1.00000E+00 0.00000E+00
 -1    5 0.00000E+00 0.00000E+00 1.00000E+00
 -1    6 1.00000E+00 0.00000E+00 1.00000E+00
 -1    7 1.00000E+00 1.00000E+00 1.00000E+00
 -1    8 0.00000E+00 1.00000E+00 1.00000E+00
 -3
    3C
 -1    1    1    1    1
 -2    1    2    3    4    5    6    7    8
 -3
   50C
 -1    1
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.00000E+00 0.10000E+01
 -1    2
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.10000E+01
 -1    3
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.20000E+01 0.10000E+01
 -1    4
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 0.10000E+01 0.00000E+00 0.20000E+01 0.10000E+01
 -1    5
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 0.20000E+01 0.00000E+00 0.20000E+01 0.10000E+01
 -1    6
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 0.20000E+01 0.00000E+00 0.10000E+01 0.10000E+01
 -3
 9999

The model geometry data sets define a cubic eight-noded brick. The Transformations Data Set then defines six transformations on the cube. Each of these transformations is a translation in this example. This model may be entered into the FEMVIEW database and then the `ASSEMBLE' command may be used at the model index level to build an assembly of transformed versions of the original cube.

The Use of Pre-defined FEMVIEW calculations

 

Principal Stress

  This example demonstrates the use of the attribute variant record in defining a principal stress data set where the order of the input data values is different to the order required in the menu. 

   100CLOADNM
  -4  P-STRESS   16    2    1
  -5  P1          1    3    1
  -5  P1COSX           3    2
  -5  P1COSY           3    3
  -5  P1COSZ           3    4
  -5  P2          1    3    1
  -5  P2COSX           3    2
  -5  P2COSY           3    3
  -5  P2COSZ           3    4
  -5  P3          1    3    1
  -5  P3COSX           3    2
  -5  P3COSY           3    3
  -5  P3COSZ           3    4
  -5  Q1          1    1         1Q1-STRES
  -5  Q2          1    1         1Q2-STRES
  -5  Q3          1    1         1Q3-STRES
  -5  QMAX        1    1         1QMAX
  -6   10   12  1  5  9  2  3  4  6  7  8 10 11 12
  -1    1    2        10
  -2    2   -- then P1, P2, P3, P1COSX, P1COSY, P1COSZ
  -2    2   -- then cosines for P2 and P3

Using Previously Input Data

  This example shows how to define attributes whose components are derived from the components of another attribute. The first defines three components, each of the vector type of magnitude plus direction cosines, which will be calculated from the first matrix components to appear in the attribute STRESS, which must be defined for the same entity type. The second is to be calculated from the same data, but in this case the result is a scalar which will be referenced by its attribute name only. 

   100CLOADNM
  -4  P-STRESS    3    2
  -5  P1          1    3              1P1-STRESSTRESS
  -5  P2          1    3              1P2-STRESSTRESS
  -5  P3          1    3              1P3-STRESSTRESS
   100CLOADNM
  -4  VONMISES    1    2
  -5                   1              1VONMISESSTRESS
  9999

The FEMVIEW pre-defined calculations can also be invoked by selecting the correct attribute type for source information and then issuing the required `RESULTS CALCULATE' command.

Homogeneous Transformation Matrix

  A homogeneous transformation matrix is a user defined result data type with a component type of 5 in the component definition records. The homogeneous transformation matrix can be used to transform matrices and vectors in FEMVIEW with the command `RESULTS CALCULATE EXPRESSION'.

For example the header record below 

  -4  TRANSFRM   16    1    1
  -5  RXX         1    5    1    1
  -5  RYX         1    5    2    1
  -5  RZX         1    5    3    1
  -5  PX          1    5    4    1
  -5  RXY         1    5    1    2
  -5  RYY         1    5    2    2
  -5  RZY         1    5    3    2
  -5  PY          1    5    4    2
  -5  RXZ         1    5    1    3
  -5  RYZ         1    5    2    3
  -5  RZZ         1    5    3    3
  -5  PZ          1    5    4    3
  -5  TX          1    5    1    4
  -5  TY          1    5    2    4
  -5  TZ          1    5    3    4
  -5  SCALE       1    5    4    4
  -6    1   16  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16

gives the matrix:

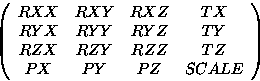
\begin{displaymath} \left( \begin{array} {cccc} RXX & RXY & RXZ & TX\\ RYX & R... ...ZX & RZY & RZZ & TZ\\ PX & PY & PZ & SCALE\end{array} \right) \end{displaymath}

where Rij are the rotation terms, Ti are translation terms, Pj are perspective terms, and SCALE is an overall scale factor.

It is not necessary to define all terms as when used in calculations the missing terms will be taken as if a unit matrix . For example if only the rotational terms are given 

  -4  TRANSFRM    9    1    1
  -5  RXX         1    5    1    1
  -5  RYX         1    5    2    1
  -5  RZX         1    5    3    1
  -5  RXY         1    5    1    2
  -5  RYY         1    5    2    2
  -5  RZY         1    5    3    2
  -5  RXZ         1    5    1    3
  -5  RYZ         1    5    2    3
  -5  RZZ         1    5    3    3
  -6    1    9  1  2  3  4  5  6  7  8  9

the resulting matrix will be:

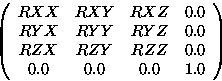
\begin{displaymath} \left( \begin{array} {cccc} RXX&RXY&RXZ&0.0\\ RYX&RYY&RYZ&0.0\\ RZX&RZY&RZZ&0.0\\ 0.0&0.0&0.0&1.0\end{array} \right) \end{displaymath}

VECTORs are expanded to the homgeneous form:

\begin{displaymath} \left( \begin{array} {cccc} X & Y & Z & 1.0 \end{array} \right) \end{displaymath}

For the purpose of matrix operations vectors are either row or column depending on the order of the operands, see the RESULTS CALCULATE EXPRESSION command.

Notes:

1.
Care should be taken with non-zero perspective terms.
2.
This user defined form is intended for MATRIX MULT VECTOR operations alternative definitions are possible.

Assembly Definitions Data Sets

  This example illustrates the way in which Assembly Definition Data Sets may be used to define an assembly as the sum of two simple models. 

    1CPLATE1
    2C
 -1    1 0.00000E+00 0.00000E+00 0.00000E+00
 -1    2 1.00000E+00 0.00000E+00 0.00000E+00
 -1    3 1.00000E+00 1.00000E+00 0.00000E+00
 -1    4 0.00000E+00 1.00000E+00 0.00000E+00
 -1    5 2.00000E+00 0.00000E+00 0.00000E+00
 -1    6 2.00000E+00 1.00000E+00 0.00000E+00
 -3
    3C
 -1    1    9    0    0
 -2    1    2    3    4
 -1    2    9    0    0
 -2    2    5    6    3
 -3
   50C
 -1    1
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 0.00000E+00 2.00000E+00 0.00000E+00 0.10000E+01
 -3
  100CL1     0.00000E+00            RES FOR PLATE1       0    0STATIC
 -4  DISPLACE    1    1    0
 -5  X           1    1    0    0    0
 -1    1 1.00000E+00
 -1    2 1.00000E+00
 -1    3 1.00000E+00
 -1    4 1.00000E+00
 -1    5 1.00000E+00
 -1    6 1.00000E+00
 -3
    1CPLATE2
    2C
 -1   11 0.00000E+00 0.00000E+00 0.00000E+00
 -1   12 1.00000E+00 0.00000E+00 0.00000E+00
 -1   13 1.00000E+00 1.00000E+00 0.00000E+00
 -1   14 0.00000E+00 1.00000E+00 0.00000E+00
 -3
    3C
 -1    1    9    0    0
 -2   11   12   13   14
 -3
   50C
 -1    1
 -2 0.10000E+01 0.00000E+00 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.10000E+01 0.00000E+00 0.00000E+00
 -2 0.00000E+00 0.00000E+00 0.10000E+01 0.00000E+00
 -2 5.00000E+00 0.00000E+00 0.00000E+00 0.10000E+01
 -3
  100CL1     0.00000E+00            RES FOR PLATE2       0    0STATIC
 -4  DISPLACE    1    1    0
 -5  X           1    1    0    0    0
 -1   11 2.00000E+00
 -1   12 2.00000E+00
 -1   13 2.00000E+00
 -1   14 2.00000E+00
 -3
    1BASSEM
 -1 PLATE1
 -1 PLATE1    1
 -1 PLATE2
 -1 PLATE2    1
 -3
 9999

Notes:

1.
If it was desired to locate assembly `ASSEM' in another assembly, and transform it, a Transformations Data Set would have to be included under 'ASSEM' at any point after the Assembly Definition Data Set.
next up previous contents index
Next: Element Types Up: Format of the neutral Previous: Pre-defined FEMVIEW Calculations

Femsys Limited
17th August 1999