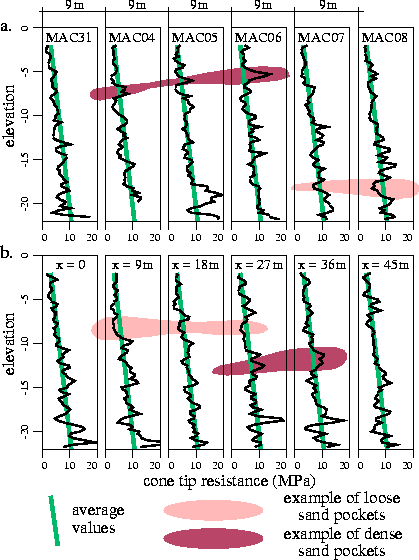
Figure 3: Comparison between: a. in-situ recorded cone tip resistances (Gulf (1984)), and b. simulated values obtained at the same locations from one sample function.
Experimental evidence shows that there is natural variability of soil properties within distinct and uniform layers. Even in case of supposedly homogeneous man- made fills, this variability is strongly manifested, as illustrated in Fig. 3a by the results of a series of piezocone tests performed for a hydraulically placed sand (Gulf (1984)): recorded cone resistance exhibits random fluctuations about some average values shown with thick lines in Fig. 3.

Figure 3: Comparison between: a. in-situ recorded
cone tip resistances
(Gulf (1984)), and b.
simulated values obtained at the same locations from one sample
function.
As expected, some degree of coherence between the fluctuations can be observed, which becomes stronger as the measuring points are closer together. This is illustrated in Fig. 3a by the presence of loose pockets (where recorded values are consistently lower than the expected average) and dense pockets in the soil mass. This spatial coherence is mathematically captured by the concept of correlation function, with its parameters expressed in terms of ``correlation distances''. The correlation distance can be thought as representing a length over which significant coherence is still manifested.
The probability distribution function of soil properties is another important characteristic of spatial variability. For the fluctuations of cone tip resistance shown in Fig. 3a, a skewed Beta distribution was found to fit the empirical distribution of the field test results.
Whenever simultaneous field measurements are available (e.g. piezocone tests provide cone tip resistance, sleeve friction and dynamic pore pressure) it is possible to estimate the cross-correlation between various soil properties. Consequently, the assembly of field test results over the domain of interest can be viewed as a multi-variate, multi-dimensional (mV-nD), non-Gaus- sian stochastic field, each scalar component of the vector field representing one of the relevant soil properties. The probabilistic characteristics of the stochastic field are (Fig. 1b): (1) the cross-correlation structure, represented in the wave-number domain as a cross-spectral density matrix, and (2) the probability distribution function of each component. For a detailed presentation of field data analysis procedures leading to estimation of probabilistic characteristics of spatial variability, the reader is referred to Popescu et al (1997b).
For the case when available field data is inadequate for stochastic analysis (e.g. when the sampling distance is larger than the expected correlation distance), the user can rely on information obtained from soil deposits with similar characteristics, which is stored in a database. Conversely, the database is updated every time a new stochastic analysis is performed based on a significant set of field test results.