Taylor-Couette Flows and Instability
This page is still under construction. For more info contact Arel Weisberg
To learn more about research in Taylor-Couette flow phenomena going on at the Gas Dynamics Lab click here
The Taylor-Couette experiment consists of a fluid in the gap between two infinitely long concentric cylinders, one or both of which are rotating along their common axis. The resulting fluid flow is called Taylor-Couette flow. An analytical solution to the Navier-Stokes equations for this system can easily be found, but this solution is not stable for all operating conditions.
G.I. Taylor in his ground breaking 1923 paper Stability of a viscous liquid contained between two rotating cylinders analytically and experimentally determined when the Taylor-Couette system is stable for the case of the outer cylinder at rest and the inner cylinder spinning. He found that when a parameter, now known as the Taylor number, rises above a threshold value of 1708, and the gap between the cylinders is much smaller than their radii, the flow is unstable. Usually, one merely increases the rate at which the inner cylinder spins to raise the Taylor number.
The streamlines of low Taylor number T-C flow are circular. This means that if you were to insert a needle with dye into the flow, the dye would trace out a circular path. If we use water as our working fluid and mix it with some Kalliroscope solution we can easily visualize the flow. If we view this flow from a radial viewpoint, we see the following picture (the ruler is inserted for scale):

However, once the flow becomes unstable the picture radically changes. The flow becomes dominated by large toroidal vortices, stacked one on top of the other, called Taylor vortices. A cross sectional view of the flow field looks like:
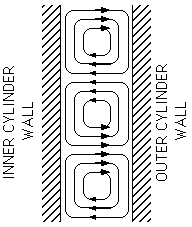
Using the Kalliroscope flow visualization method, the flow field looks like:

It is important to realize that while the first flow field was unstable at Taylor numbers of about 1708, this new flow field is stable at this point. The flow has reached a new, totally different, steady state. We reached this new state, just by slightly changing the rotation rate of the inner cylinder so that the Taylor number rose above 1708.
By further speeding up the inner cylinder (i.e. raising the Taylor number) other flow fields can be created. The final state is reached when the fluid between the cylinders is completely turbulent.