DESCRIPTIVE STATISTICS USING EXCEL AND STATA

(Excel 2003 and Stata 10.0+)

If you do not see the menu on the left click here to see it

These notes are meant to provide a general overview on how to input data in Excel and Stata and how to perform basic data analysis by looking at some descriptive statistics using both programs.

Excel

To open Excel in windows go Start -- Programs -- Microsoft Office -- Excel

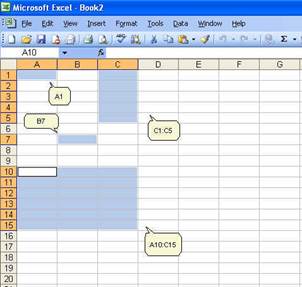
When it opens you will see a blank worksheet, which consists of alphabetically titled columns and numbered rows. Each cell is referenced by its coordinates of columns and rows, for example A1 is the cell located in column A and row 1; B7 is the cell in column B and row 7. You can reference a range of cells, for example C1:C5 are cells in columns C and rows 1 to 5. You can also reference a matrix, A10:C15, are cells in columns A, B and C and rows 10 to 15.

Excel has 256 columns and 65,536 rows.

There are some shortcuts to move within the current sheet:

· "Home" moves to the first column in the current row

· "End -- Right Arrow" moves to the last filled cell in the current row

· "End - Down Arrow" moves to the last filled cell in the current column

· "Ctrl-Home" moves to cell A1

· "Ctrl-End" moves to the last cell in your document (not the last cell of the current sheet)

· "Ctrl-Shift-End" selects everything between the active cell to the last cell in the document

To select a cell :

· Click on a cell (i.e. A10), hold the shift key, click on another cell (C15) to select the cells between A10 and C15.

· You can also click on a cell and drag the mouse to the desire range

· To select not-adjacent cells, click on a cell, press ctrl and select another cell or range of cells.

Excel stores your work in a workbook, each workbook has one or more worksheets (and/or charts) which you can view by clicking on the sheet tab (lower left corner of the active (current) sheet).

Entering data

You can type anything on a cell, in general you can enter text (or labels), numbers, formulas (starting with the "=" sign), and logical values (as in "true" or "false").

Click on a cell and start typing, once you finish typing press "enter" (to move to the next cell below) or "tab" (to move to the next cell to the right)

You can write long sentences in one single cell but you may see it partially depending on the column width of the cell (and whether the adjacent column is full). To adjust the width of a column go to Format -- Column -- Width or select "AutoFit Selection".

Numbers are assumed to be positive, if you need to enter a negative value use the minus sign ("-") or enclose the number in parentheses ("(number)").

If you need to enter percentages, dollar sign, or any other symbol to identify the number just add the "%" or "$". You can also enter the number and change its format using the menu: Format -- Cell and select the "number" tab which has all the different formats.

Dates are automatically stored as mm/dd/yyyy (or the default format if changed) but there is some flexibility here. Enter month and number and excel will enter the date in the default format. If you press "ctrl" and ";" (Crtl-;) excel will enter the current date.

Time is also entered in a default format. Enter "5 pm", excel will write "5:00 PM". To enter the current time press "ctrl" and ":" (Ctrl-:)

To practice enter the following table (these data are made-up, not real)

Each column has a list of items. Column A has IDs, column B has last names of students and so on.

Let"s say for example you do not want capital letters for the columns "Last Name" and "First Name". You do not want "SMITH" you want "Smith". Two options, you can re-type all the names or you can use the following formula (IMPORTANT: All formulas start with the equal "=" sign):

=PROPER(cell with the text you want to change)

To get the full table:Click here to get it.

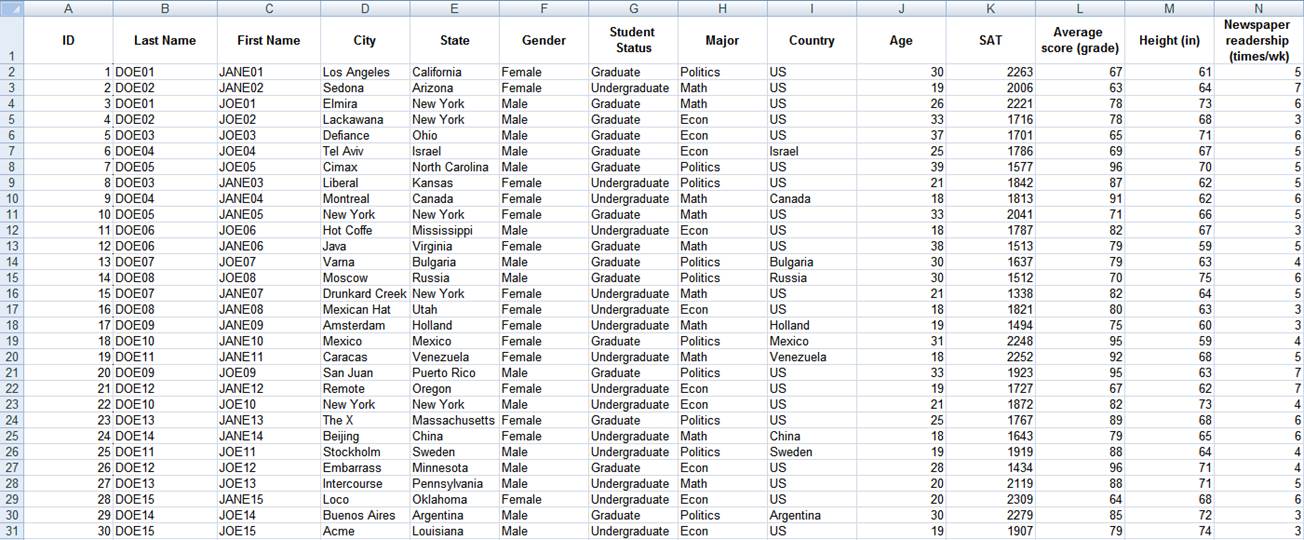
The full table should look like this. This is a made up table, it is just a collection of random info and data.

Exploring data in excel

Descriptive statistics (using excel"s data analysis tool)

Generally one of the first things to do with new data is to get to know it by asking some general questions like but not limited to the following:

· What variables are included? What information are we getting?

· What is the format of the variables: string, numeric, etc.?

· What type of variables: categorical, continuous, and discrete?

· Is this sample or population data?

After looking at the data you may want to know

· How many males/females?

· What is the average age?

· How many undergraduate/graduates students?

· What is the average SAT score? It is the same for graduates and undergraduates?

· Who reads the newspaper more frequently: men or women?

You can start answering some of these questions by looking directly at the table, for some other questions you may have to do some calculations by obtaining a set of descriptive statistics. These statistics are a collection of measurements of two things: location and variability. Location tells you the central value (the mean is the most common measure of this) of your variables. Variability refers to the spread of the data from the center value (i.e. variance, standard deviation). Statistics is basically the study of what causes such variability.

Location	Variability
Mean	Variance
Mode	Standard deviation
Median	Range

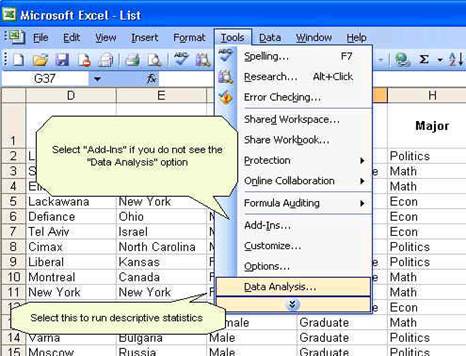
Let"s get some descriptive statistics for this data. In excel go to Tools -- Data Analysis. If you do not see "data analysis" option you need to install it, go to Tools -- Add-Ins, a window will pop-up and check the "Analysis ToolPack" option, then press OK. Try running data analysis again.

For Excel 2007 see http://office.microsoft.com/en-us/excel/HP100215691033.aspx

For Excel 2003 see http://office.microsoft.com/en-us/excel/HP011277241033.aspx

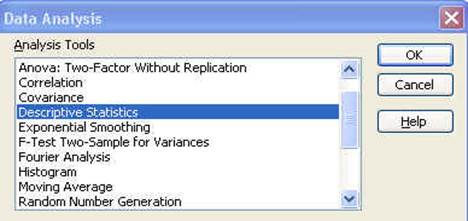
In the pop-up window select "Descriptive Statistics" click OK.

Another window will pop-up

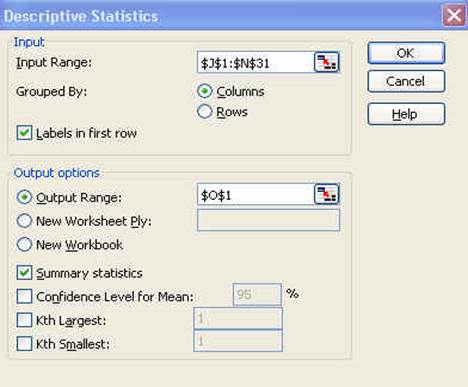
Let"s check this window:

Input Range: This is to select the data you want to analyze.

Once you click in the input range you need to select the cells you want to analyze.

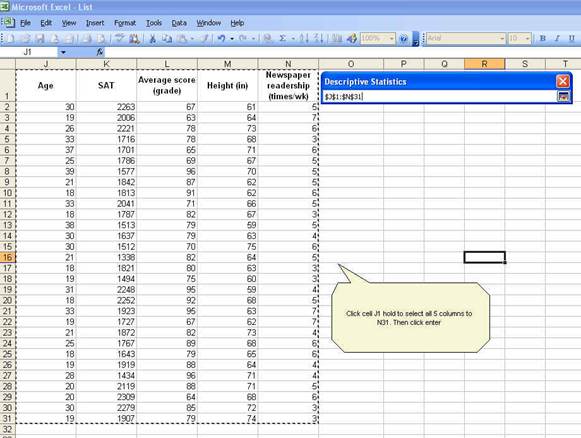
Back to the window

Since we include the labels in first row make sure to check that option. For the output option which is the place where excel will enter the results select O1 or you can select a new worksheet or even new workbook.

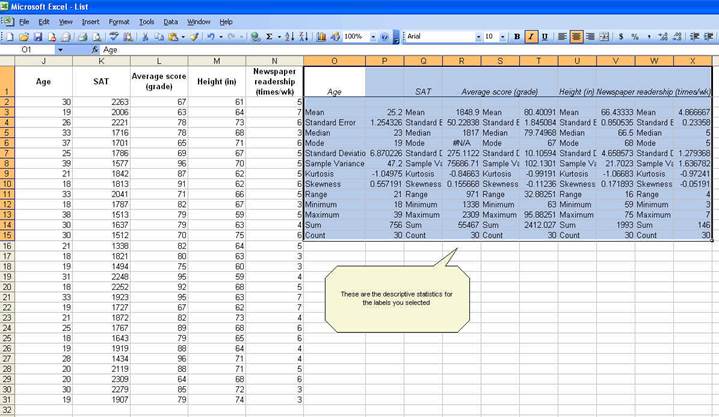
Check "Summary statistics" and the press OK. You will get the following:

While the whole descriptive statistics cells are selected go to Format--Cells to change all numbers to have one decimal point. When you get the "format cells" window, select the following:

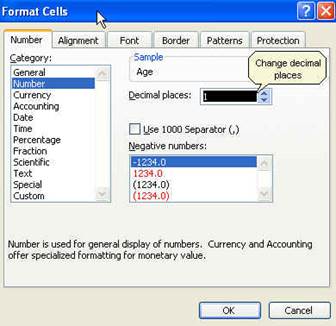
Click OK. All numbers should now have one decimal as follows:

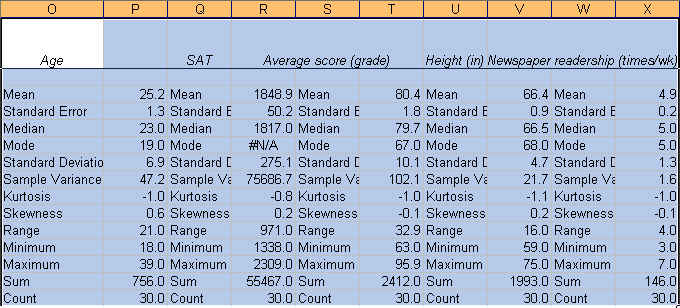
Now we know something about our data.

The average student in this sample is 25.2 years, has a SAT score of 1848.9, got a grade of 80.4, is 66.4 inches tall and reads the newspaper 4.9 times a week. We know this by looking at the "mean" value on each variable.

The mean is the sum of the observations divided by the total number of observations. It is the most common indicator of central tendency of a variable. If you look at the last two rows: "Sum" and "Count" you can estimate the mean dividing "Sum" by "Count" (sum/count). You can also calculate the mean using the function below (IMPORTANT: All functions start with the equal "=" sign):

=AVERAGE(range of cells with the values of interest)

For "age"

=AVERAGE(J2:J31)

"Sum" refers to the sum of all the values in a range of values. For age means the sum of the ages of all students. The excel function for sum is:

=SUM(range of cells with the values of interest)

"Count" refers to the count of cell that contain values (numbers). The function is:

=COUNT(range of cells with the values of interest)

"Min" is the lowest value in an array of values. The function is:

=MIN(range of cells with the values of interest)

"Max" is the largest value in an array of values. The function is:

=MAX(range of cells with the values of interest)

The "Standard Error" (SE) indicates how close the sample mean is from the "true" population mean. The average age of 25.2 years is just an estimate of this sample of students but it can vary had you used a different set of students. The standard error is calculated by dividing the standard deviation of the population (or the sample) by the square root of the total number of observations. The SE can be used to roughly define a range of certainty for the mean. Using "age":

Z	% Certainty	Lower bound	Upper bound
1 (0.99)	68%	23.9	26.5
2 (1.96)	95%	22.7	27.7
3 (2.58)	99%	21.4	29.0

Lower: Mean--(SE*Z) for example 25.2--(1.3 * 2) = 22.7

Upper: Mean + (SE*Z) for example 25.2 + (1.3 * 2) = 27.7

· You are 68% certain that the average age is between 23.9 and 26.5 years old

· You are 95% certain that the average age is between 22.7 and 27.7 years old

· You are 99% certain that the average age is between 21.4 and 29.0 years old

Note that the more certainty wider the gap.

The median is another measure of central tendency. To get the median you have to order the data from lowest to highest. The median is the number in the middle. If the number of cases is odd the median is the single value, for an even number of cases the median is the average of the two numbers in the middle. The excel function is:

=MEDIAN(range of cells with the values of interest)

The mode refers to the most frequent, repeated or common number in the data. By age there are more students 19 years old in the sample than any other group. In the SAT scores the mode is "#N/A" which means that all values are unique. The excel function is:

=MODE(range of cells with the values of interest)

Range is a measure of dispersion. It is simple the difference between the largest and smallest value, "max"--"min".

The sample variance measures the dispersion of the data from the mean. It is the simple mean of the squared distance from the mean. It is calculated by:

SV = sum of (X-mean of X)² / Number of observation minus 1

Higher variance means more dispersion from the mean. The excel function is:

=VAR(range of cells with the values of interest)

The standard deviation is the squared root of the variance. Indicates how close the data is to the mean. Assuming a normal distribution, 68% of the values are within 1 sd from the mean, 95% within 2 sd and 99% within 3 sd. The excel formula is:

=STDEV(range of cells with the values of interest)

Skewness measures the asymmetry of the data, when in an otherwise normal curve one of the tails is longer than the other. It is a roughly test for normality in the data (by dividing it by the SE). If it is positive there is more data on the left side of the curve (right skewed, the median and the mode are lower than the mean). A negative value indicates that the mass of the data is concentrated on the right of the curve (left tail is longer, left skewed, the median and the mode are higher than the mean). A normal distribution has a skew of 0. Skewness can also be estimated with the following function:

=SKEW(range of cells with the values of interest)

Kurtosis. The current view of kurtosis argues that it measures the peak of a distribution. According to Peter Westfall, that view is not quite correct. His article "Kurtosis as Peakedness, 1905--2014. R.I.P." (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC4321753/) makes a compelling case against the current perception. In Westfall"s view, the peak, or lack-thereof, is a symptom rather than a characteristic that shows the presence of outliers. High kurtosis may suggest the presence of outliers. Technically speaking, kurtosis focuses more on the tails for the distribution than the peak, so positive kurtosis indicates too few cases in the tails or a tall distribution (leptokurtic), negative kurtosis too many cases in the tails or a flat distribution (platykurtic). A normal distribution has a kurtosis of 0 (given a correction of -3, otherwise it will have a kurtosis of 3). The excel function for kurtosis is:

=KURT(range of cells with the values of interest)

--Thank you to Peter Westfall for useful feedback.

Exploring data using pivot tables

To explore the data by groups you can sort the columns for the variables you want (for example gender, or major or country, etc.) and obtain descriptive statistics by selecting only the range of values that cover particular group. You can also use pivot tables.

Let"s say you are interested on looking at the average SAT score by gender and student"s major. Let"s make the following crosstabulation

In the excel menu go to Menu--PivtoTable and PivotChart Report:

The pivot wizard will walk you through the process, this is the first window

Press "Next". In step 2 select the range for the range of all values as in the following picture:

In step 3 select "New worksheet" and press "Layout"

This is where you make the pivot table:

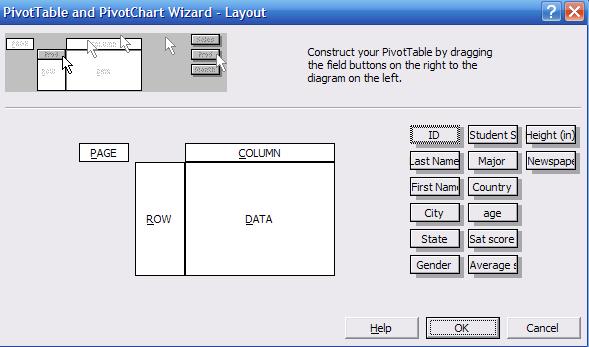
On the right side of the wizard layout you can see the list of all variables in the data. Click and drag "Gender" into the "ROW" area. Click and drag "Major" into the "COLUMN" area, and click and drag "Sat score" into the "DATA" area. The wizard layout should look like this:

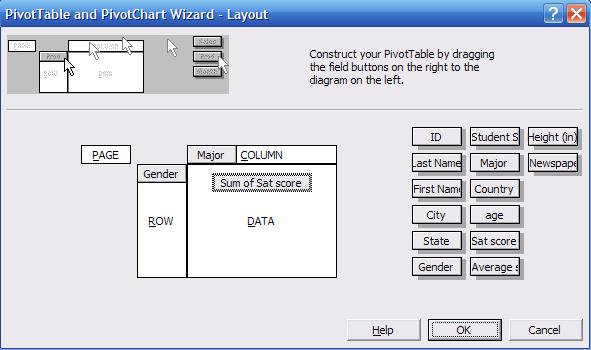
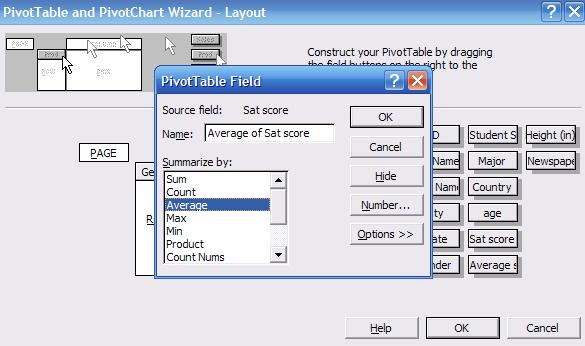
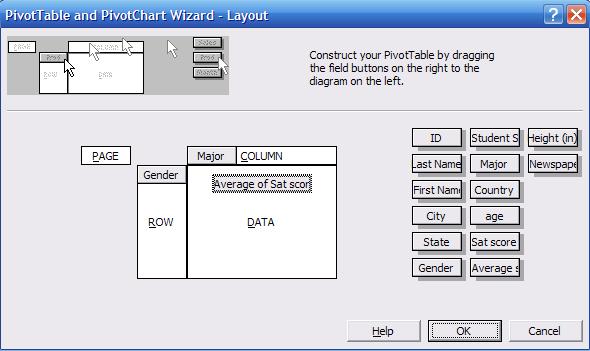
In the "DATA" area double-click on "Sum of Sat score", a new window will pop-up select "Average" and click OK.

The wizard layout should look like this. Click OK, in the wizard window step 3 click "Finish"

In a new worksheet you will see the following (the pivot table window was moved to save some space).

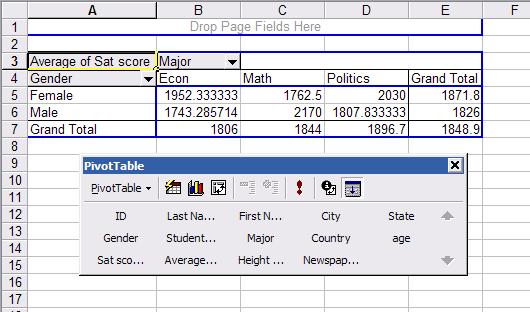
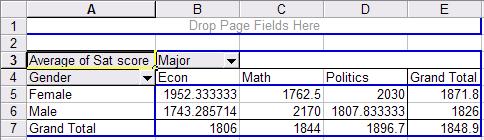
This is a crosstabulation between gender and major. Each cell represents the average SAT score for a student according to gender and major. For example a female student with an econ major has an average SAT score of 1952 (cell B5 in the picture) while a male student also with an econ major has 1743 (B6). Overall econ major students have an average SAT score of 1806 (B7) . In general, female students have an average SAT score in this sample of 1871.8 (E5) while male students 1826 (E6).

For more information on pivot tables go to the following site.

http://www.microsoft.com/dynamics/using/excel_pivot_tables_collins.mspx

For graphing in excel we recommend the following links.

(Histograms)

http://office.microsoft.com/en-us/excel/HA011109481033.aspx

(Histograms)

http://www.physics.upenn.edu/~uglabs/Histograms-with-Excel.pdf

http://www.fgcu.edu/support/office2000/excel/charts.html

http://www.csubak.edu/~jross/classes/GS390/Spreadsheets/ExcelCharts/CreateChart.htm

http://www.ncsu.edu/labwrite/res/gt/gt-bar-home.html

(Error bars)

http://peltiertech.com/Excel/ChartsHowTo/ErrorBars.html

(Error bars)

http://mtsu32.mtsu.edu:11009/Graphing_Guides/Excel_Guide_Line_Means.htm

One-way ANOVA using excel

Let"s say you want to explore whether there is a relationship between the average score (grade) of each student and his/her major. In the sample we have three majors: Econ, Math and Politics. The grades are the final grades for the entire academic year.

To do this we use one-way ANOVA, which stands for "analysis of variance". ANOVA "is a broad class of techniques for identifying and measuring the various sources of variation within a collection of data" (Kachigan, p. 273, 1986). It is closely related to regression analysis but with the following difference: "[w]e can think of the analysis of variance technique as testing hypotheses about the presence of relationships between predictor and criterion variables, regression analysis as describing the nature of those relationships, and r² as measuring the strength of the relationships" (ibidem.) In other words, ANOVA "tests whether the means of y [grades in this example] differ across categories of x [majors]" (Hamilton, p. 149)

With the above in mind, let"s see if there is a relationship between student"s majors and student"s final grades. First we need to rearrange the data so excel can run the ANOVA. Using only the columns "major" and "average score (grade)". Copy and paste both columns into a new sheet, sort by major (Data--Sort, select the column for major and sort ascending) separate by group. Final table should look like this..

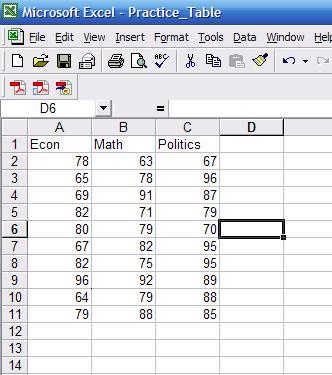
Go to Tools -- Data Analysis, in the pop-up window select "Anova: Single Factor", the following screen will pop-up

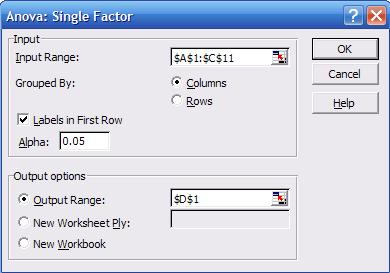
It looks similar to the one we got when we obtained "descriptive statistics". Select the input range, check "labels in First Row", and select as output range "D1", click OK. You"ll get the following:

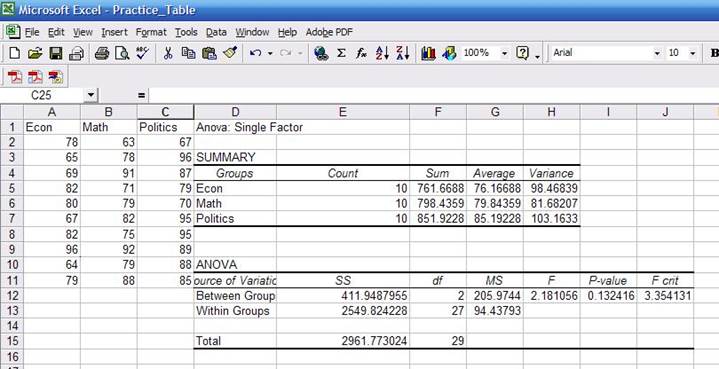
By now you should be familiar with the summary statistics presented in the first table. You may notice that the "sum" column has decimals while the data seems to be integers. The sum has decimals because some of the scores have decimals; they are just rounded to the nearest integer.

In the ANOVA table:

· Sources of variation. The analysis of variance requires the estimation of two variances: between groups (econ, math and politics) and the within groups (students).

· SS. Sum of square deviations

· df. Degrees of freedom. For between groups is 2 (number of majors minus 1) and for within groups is 27 (number of students minus number of majors).

· MS. Mean square of deviations (variance estimates), which is equal to SS/df, Roughly 411/2 and 2549/27.

· F. Is a probability distribution. It is the ratio of two variances. Roughly 205/94=2.18. According to Kachigan, the F is the ratio of:

· P-value. This is the value that answers your question. We wanted to know whether there is some sort of relationship between majors and grades. ANOVA assumes by default that there is no relationship. As a general rule, a p-value greater than 0.05 means ANOVA"s assumption may be right. We got a p-value of 0.13 which is greater than 0.05, so it seems there is no relation between a student"s major and his/her final grade. Had the p-value been lower than 0.05 then we would have found some kind of relationship between majors and grades.

· F-crit. It is the critical value to check whether we reject of fail to reject ANOVA"s assumption. Check the table for 0.05 confidence at http://www.statsoft.com/textbook/sttable.html#f05

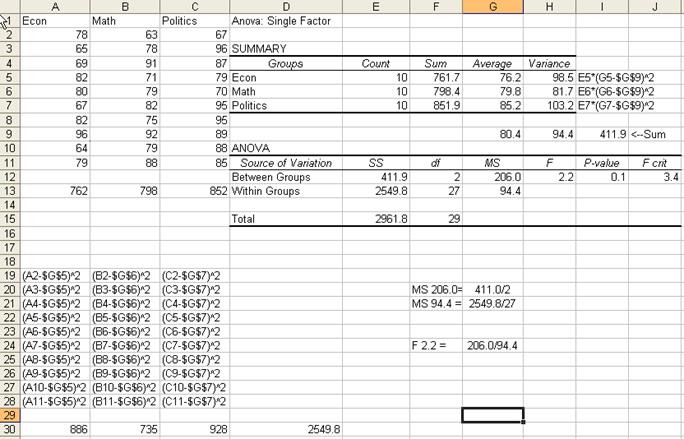
Here is a general overview on how some numbers were estimated. Follow the coordinates by columns and rows

STATA

Stata is a statistical package to help you perform data analysis, data manipulation and graphics.

To open Stata go to Start -- Programs -- Stata[ver.*] -- Stata[*]. For cluster computers contact OIT for instructions. When you open Stata this is what you will see:

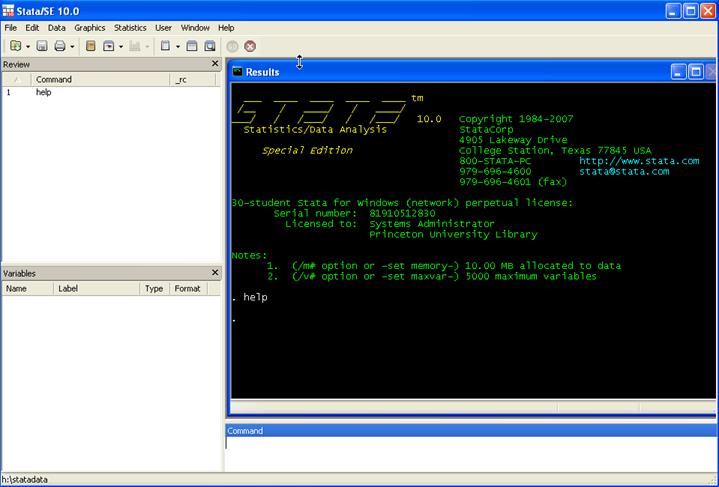
Here are some brief explanations.

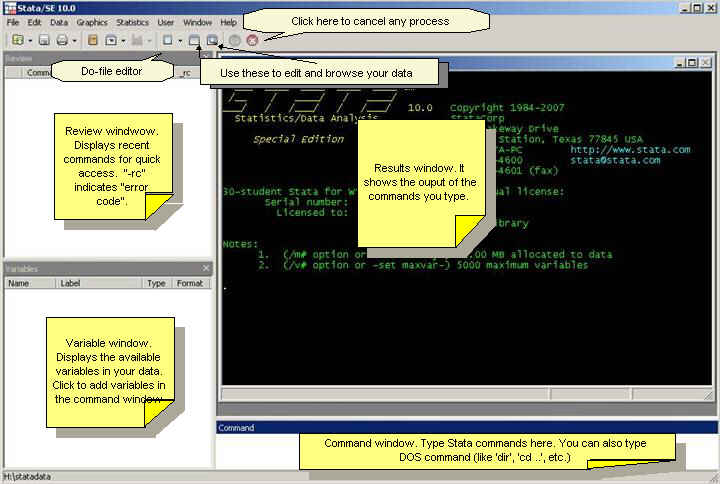
You can always use the "point-and-click" method by using the menu. We recommend however, for most of the procedures, to use the command line.

When you work with Stata there are three basic procedures you may want to do first: create a log file, set your working directory, and set the correct memory allocation for your data)

The log file records everything you type and get while working in Stata. Commands and output are send to a text file for you to review later. Think of it as a "tape recorder" for your Stata session. To create a log file go to File -- Log -- Begin

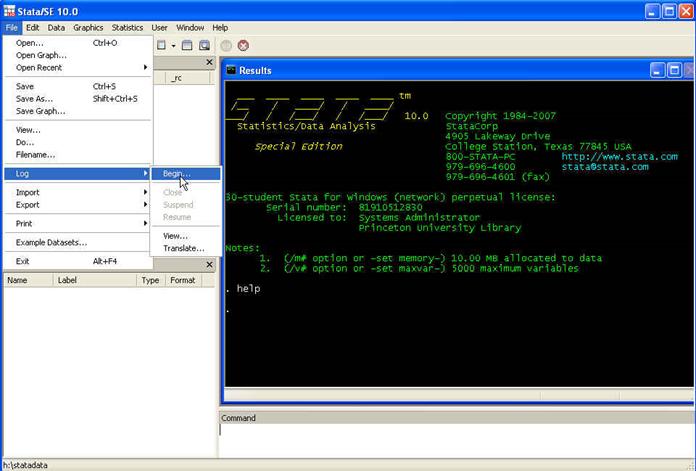
Select the working directory. In this case will be H:\statdata\. Name the log and select the type "Log (*.log)".

In the results window you will something like

The second thing to check is your working directory. To do this in the command window type the following

pwd

Which stands for "print working directory". This will show you your working directory, which right now, in this example is H:\statadata.

To see what is in that directory (good old DOS command). Type

dir

For the purposes of this course we will work in the following directory

H:\statadata\

To change directory type in the command window

cd H:\statadata\

You can check your current directory by looking at the lower left of the Stata screen.

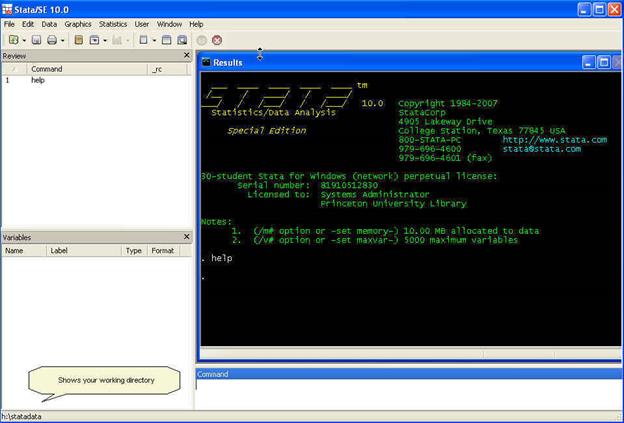
The third initial step is to set the necessary memory allocation. In the picture above you can see in green letters after "Notes:" that the memory allocation is 10 mb. This will be enough for a medium size database but sometimes you may need more memory space to store your dataset. To determine the size of your dataset follow the formula:

Size (in bytes) = (8*Number of cases or rows*(Number of variables + 8))

Depending on your Stata version and computer power, you can allocate up to around 2 gigabytes. To allocate 1 g you can type:

set mem 1g

From Excel to Stata

To put Excel data to Stata you can simply copy-and-paste.

NOTE: Not recommended for really big datasets or datasets with long string variables and lots of special characters (like ";",",","#","%", etc.)

Got to Stata, click on the "Data editor" icon

A new window will pop-up, is the data editor window where you can input data or simply paste it.

In Excel, select the whole table (A1:N31). Press Ctrl-C. Go to the "Data Editor" in Stata and paste the table (Ctrl-V)

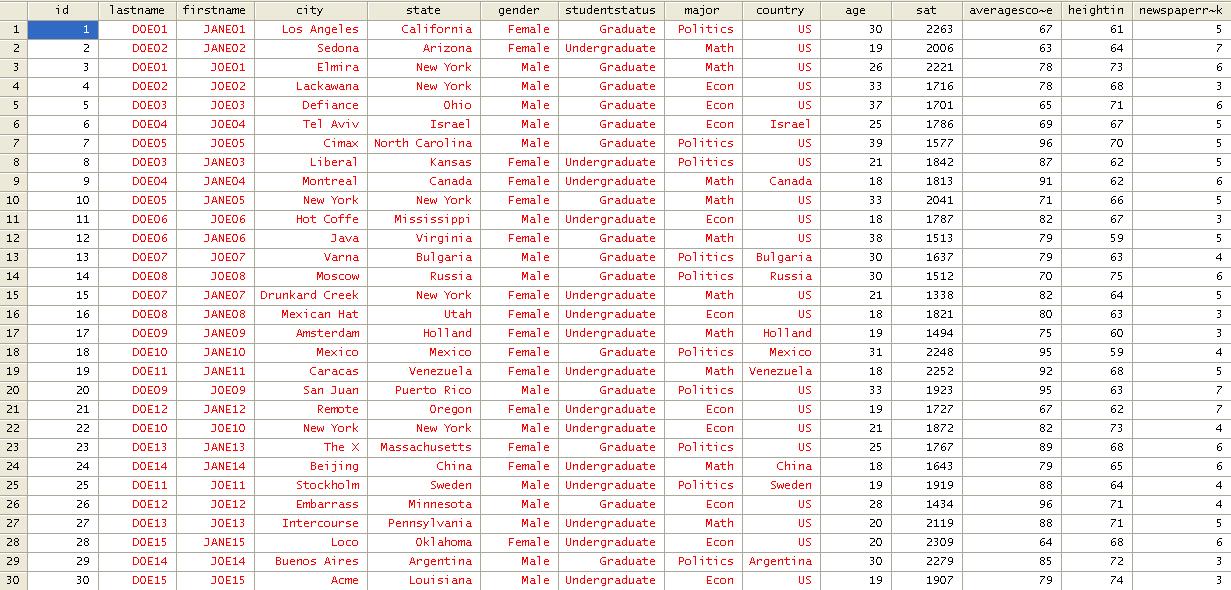
Numbers are always black. Red indicates error, in the editor"s case indicates that values are not numbers, in this case letters or string characters. Close the data editor by clicking on the "X" in the upper right corner

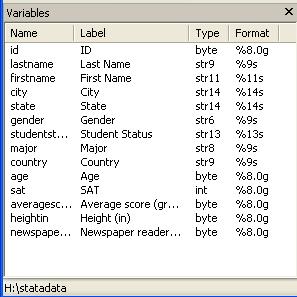
The variable window will be populated with all the variables in your data

Stata automatically eliminates the space in your original titles but keep the format in the "Label" column. "Type" refers to whether the data is number or string (str*). "Format" shows the length of the variable. In the command window type help format for details.

The whole screen will look like this

Descriptive statistics

To start exploring the data you may want to know how many graduates and undergraduates are in the sample. For this type in the command window (type help tab for more details):

Click here to get the data

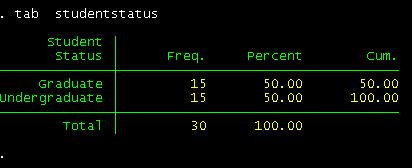
tab studentstatus

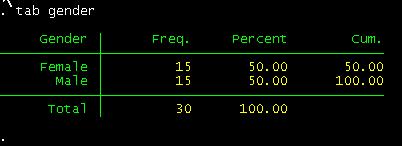
We have 15 undergrads and 15 grads.

How many females/males?

tab gender

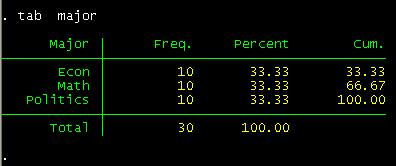
How many are econ/politics/math major?

tab major

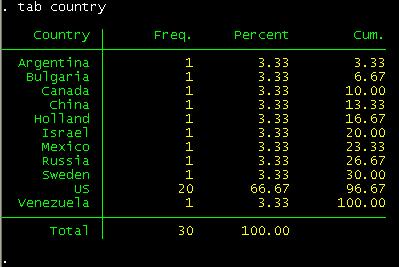
From what country?

tab country

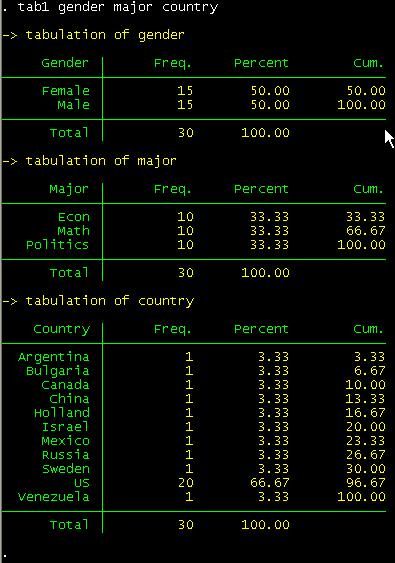
If you want to run frequencies for more than one variable at the same time use tab1 not tab.

tab1 gender major country

You should get something like this:

If you want do a crosstabulation you type:

tab major gender

This is

tab [variable by rows] [variable by column]

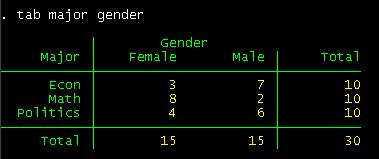
Crosstabulation shows you the subgroups formed by two variables. You can see that in the sample there are 10 econ majors 3 of which are females and 7 males. You could also say that there are 15 males 7 of which are econ major, 2 math and 6 politics.

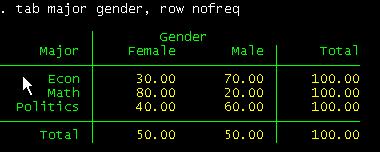
If you want percentages by major instead of counts type:

tab major gender, row nofreq

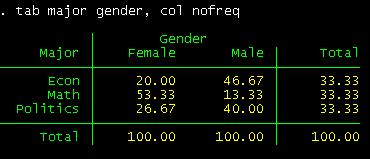
Or by column:

tab major gender, col nofreq

To see more options type help tab in the command window.

To get more information on your data we will use the commands: describe, summarize, tabstat and a combination of tab and summarize.

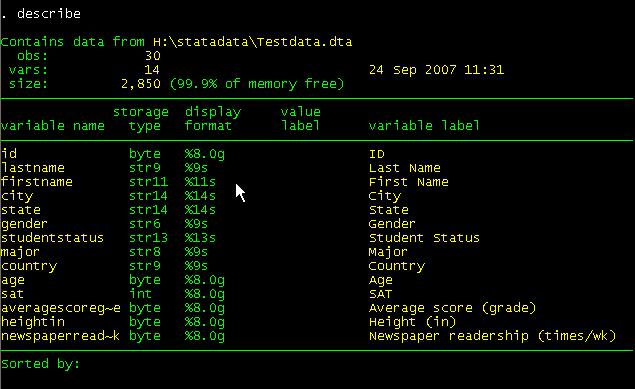
In the command window type describe. The describe command will provide you info for the active dataset and the format of the variables ("display format"). [Hit enter or spacebar to see the rest of the list]. Type help describe for further details (if the "--more-- " message bugs you, type set more off)

Summarize will provide you with some familiar descriptive statistics.

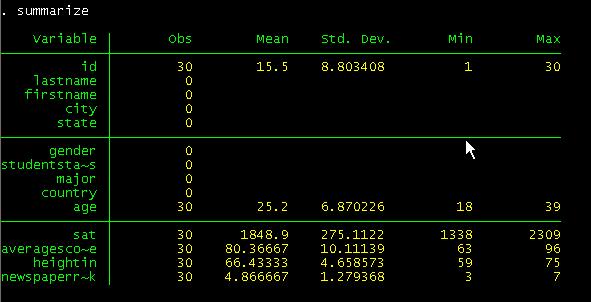
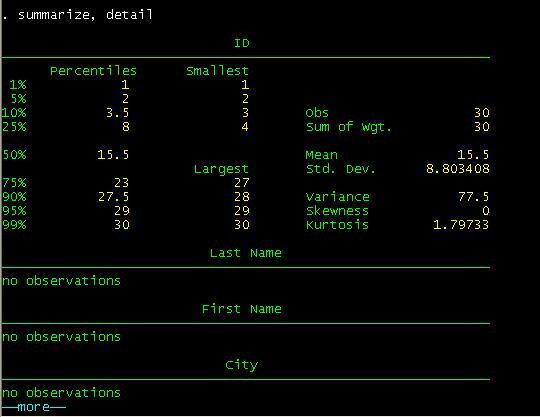
If you type summarize, detail, you will get a more detail set of statistics (press bar space to continue)

We skip some results to accommodate some in one window.

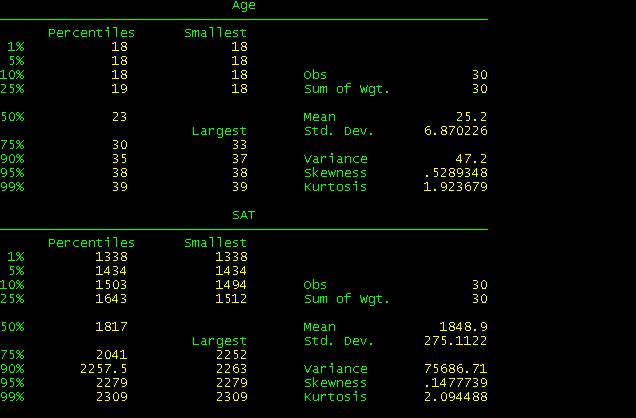
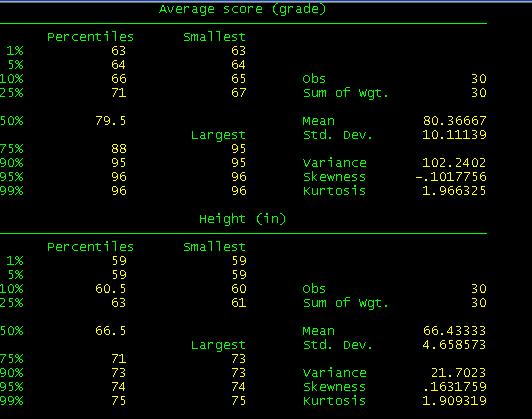
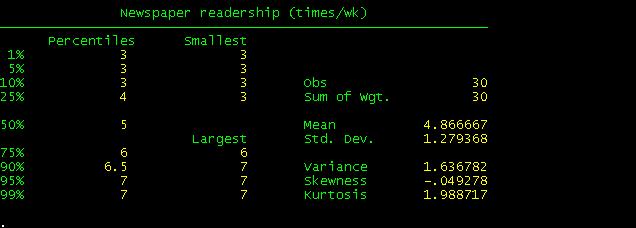
When you compare these results with the excel file you will see they are basically the same with the exception of Skewness and Kurtosis which Stata calculates differently.

Tabstat is another command that provide summary statistics

In the command line type. To fastrack type tabstat and then click on each variable in the variables windowo. The "s" before the parenthesis stands for "statistics" here you select the statistics you need.

tabstat age sat averagescoregrade heightin newspaperreadershiptimeswk, s(mean semean median sd var skew k count sum range min max )

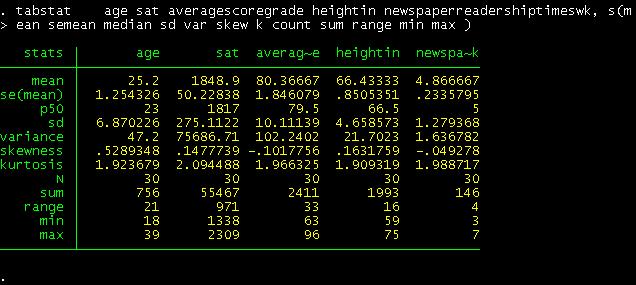
This table looks similar to the one obtained in excel. Notice that "p50" is the median.

If you are interested in getting these statistics by gender just add after the comma the option by(gender)

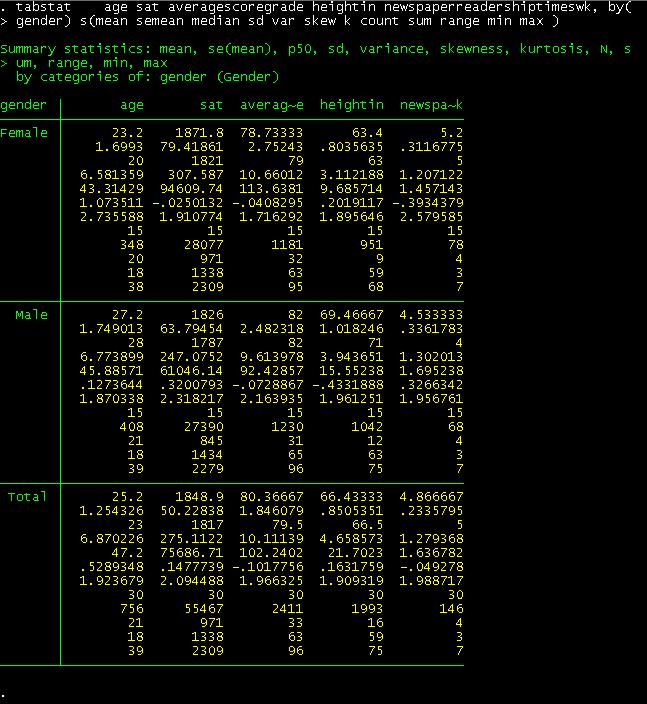
To recreate the pivot table we did in excel we just type the following:

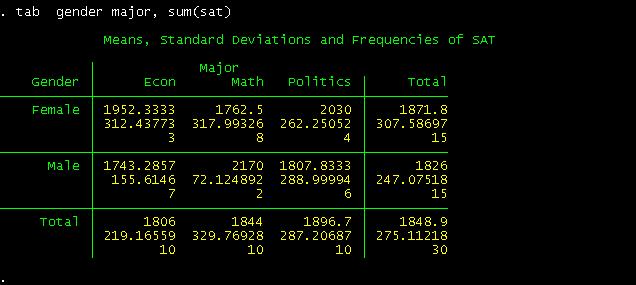
This is a crosstab between gender and student"s major regarding SAT"s scores. The following part provide us the way to read the table

For example, for the cross between females and Econ. A female student with an econ major has an average SAT score of 1952, with a standard deviation of 312 and in the sample there are only three students in this category.

Without the option sum(sat), we will get a simple crosstabulation between gender and major

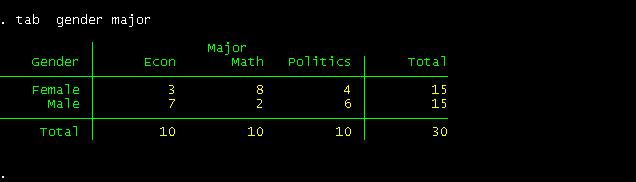
You can have more options if you want (type help tab for details). For example if you want percentage by columns and row type:

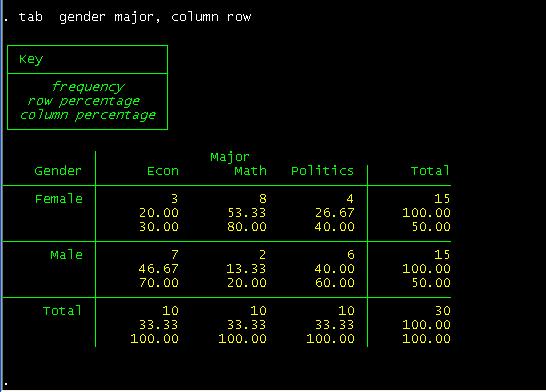
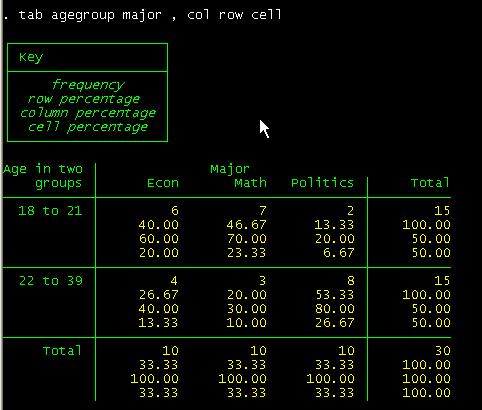
You can read this table as follows. Among female students, 20% are econ major, 53.3% are math and 26.67% are in politics.

Among econ majors, 30% are females and 70% are males.

Let"s say you wan only column percents, type

tab gender major, column nofreq

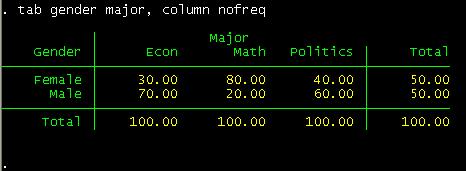
Notice the "nofreq" option.

By the way, remember the little warm-up we had in excel converting last and first names into proper format? Well, we can do that in Stata as well. The following introduces a way to generate new variables (type help generate for more details)

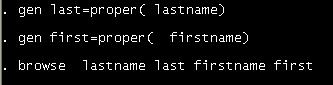
When you hit enter after browse you will see the difference.

Rolling standard deviation

*******If you do not see the menu on the left click here to see it

NOTE: Replace words in italics with your own

This will produce a rolling standard deviation every three years as indicated in the option window() below, adjust it to your desired window:

cd H:\
use http://dss.princeton.edu/training/Panel101.dta, clear

xtset country year
rolling x1_sd=r(sd), window(3) saving(x1_sd): sum x1
use x1_sd
rename end year
save, replace
use http://dss.princeton.edu/training/Panel101.dta, clear
merge 1:1 country year using x1_sd
drop _merge

For more details type

help rolling

For similar commands type

help tssmooth

ANOVA using Stata

*******If you do not see the menu on the left click here to see it

One-way ANOVA tests whether the mean of the dependent variable (y) is statistically significant among different categories of the independent variable (x). The format is

oneway [measurement] [categorical]

In the example below, we are interested on testing whether a student"s major has some effect on his/her grade. Type:

oneway averagescoregrade major, tabulate

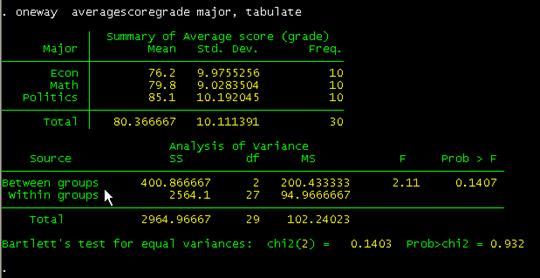
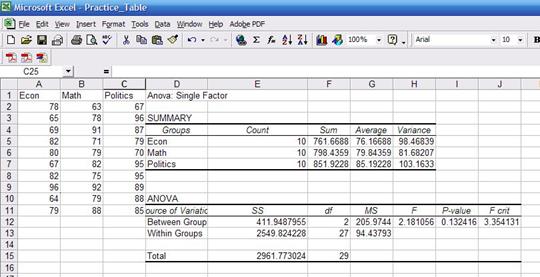
Comparing these with the results using excel (shown below) they are pretty close. "Prob>F" is the p-value which has to be lower than 0.05 (for 95% confidence) to be significant. Conclusions are basically the same.

For more details and more options type help oneway.

As an exercise run one-way ANOVA by gender.

Graphs

If you go to the menu and click "Graphics" you will see all the graphing options available in Stata. If you do not have it already, click here to get the data to do these graphs.

Let"s see one basic scatterplot. We will add some options later. Scatterplots are good to explore possible relationships between variables and to identify outliers. In this case we want to explore visually whether there is some relationship between age and SAT scores. If there is some kind of relationship we would be able to see a specific patter (linear, curve, concave, etc.). For many more bells and whistles type help scatter in the command window. The format is twoway scatter y x. For starters let"s type:

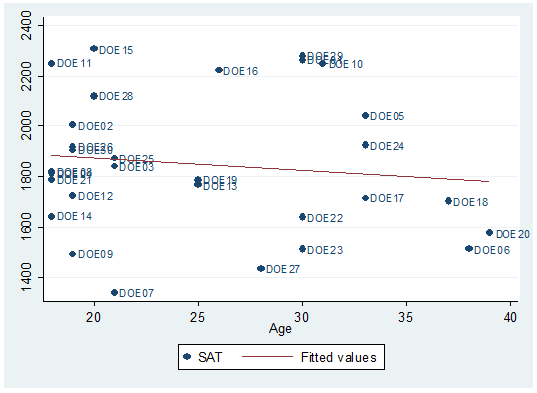
twoway scatter sat age

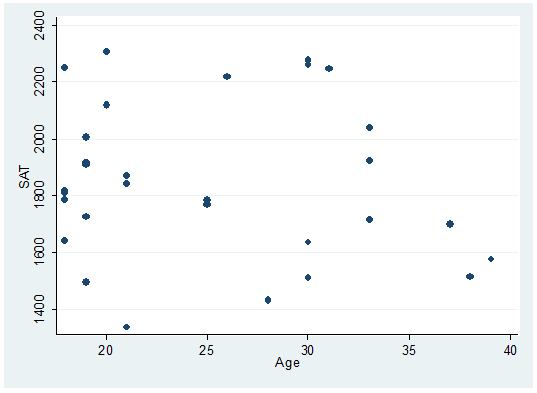
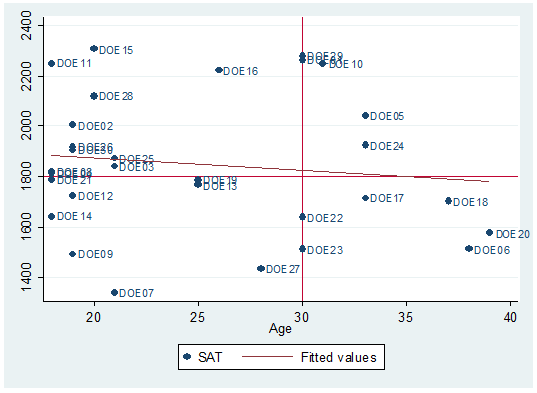
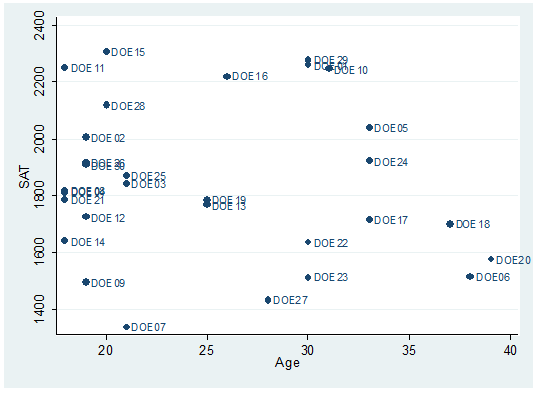
There seems to be a downward relationship, older students may show lower SAT scores. Each dot represents a student, the option mlabel below will help you identify and label the dots.

twoway scatter sat age, mlabel(lastname)

To fit a regression line type:

twoway scatter sat age, mlabel(last) || lfit sat age

You may want to add some quadrants as in the following.

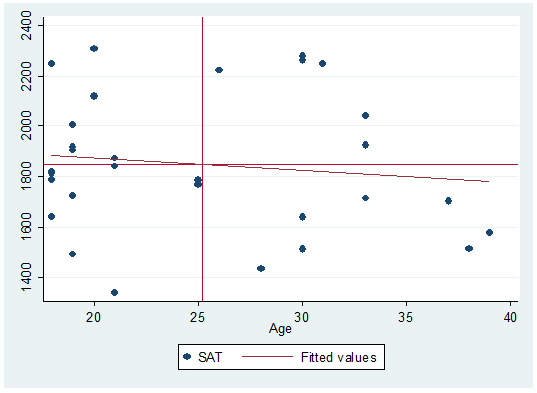
Quadrants here represent the mean of both variables. Here is how to do it:

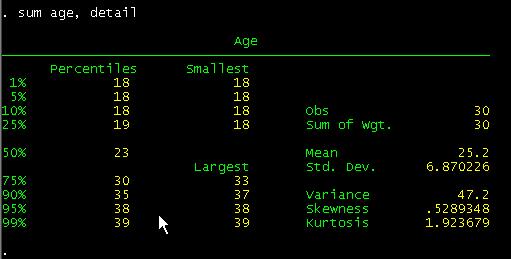
Type

sum age, detail

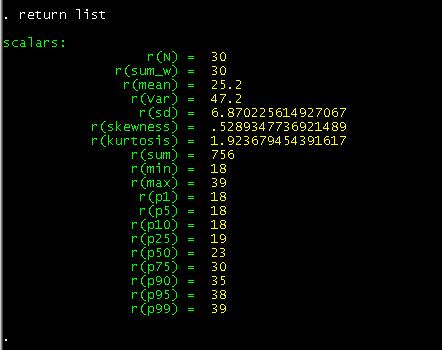
Then type:

return list

In this case we are interested in the mean of "age", so we save it as a temporary variable by typing:

local meanage=r(mean)

We do the same thing with "sat"

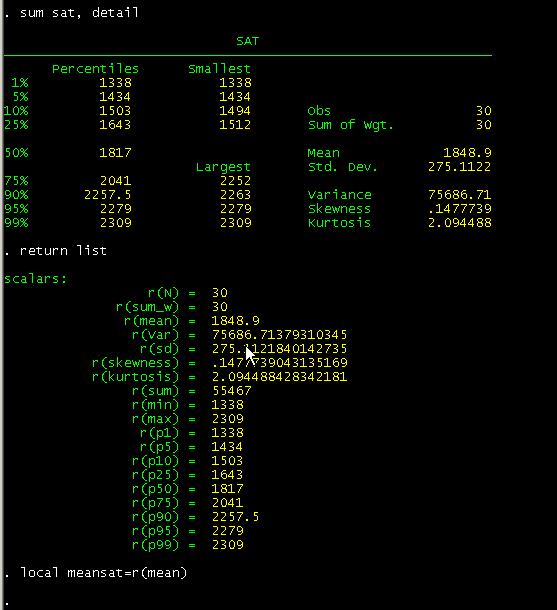
The local command is used for macros an assigns strings names to macros. In this case we create temporary variables. To make the graph with the quadrants type:

twoway scatter sat age || lfit sat age, yline(`meansat') xline(`meanage')

Notice the "yline" and "xline" options after comma and the single quotes.

If you want to set your own parameters for the quadrants just type the number in the "yline" and "xline" options. For example we want lines that cross age at 30 and SAT at 1800:

twoway scatter sat age, mlabel(lastname) || lfit sat age, yline(1800) xline(30)

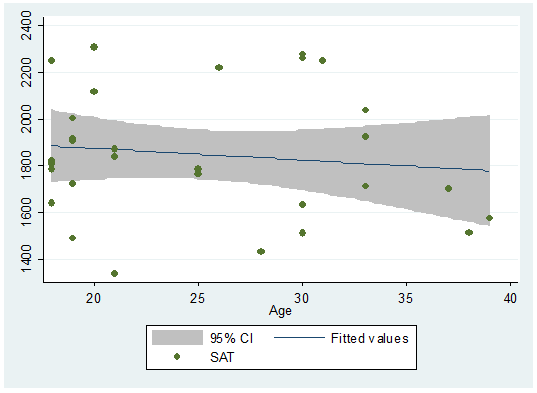
If you want to include the confidence bands we have to reverse the order of the graphs because the shaded area tends to cover the dots. So we graph the confidence region first, then the scatter.

twoway (lfitci sat age) || (scatter sat age)

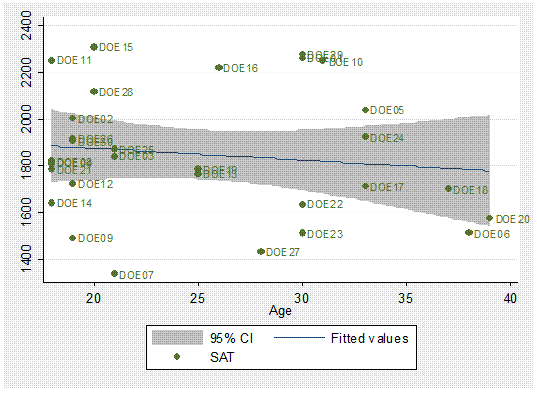
Or with labels.

twoway (lfitci sat age) || (scatter sat age, mlabel(lastname))

You may want to add a title to the graph and a title to the y-axis.

twoway (lfitci age sat) || (scatter age sat, mlabel(lastname)), title("SAT scores by age") ytitle("Age")

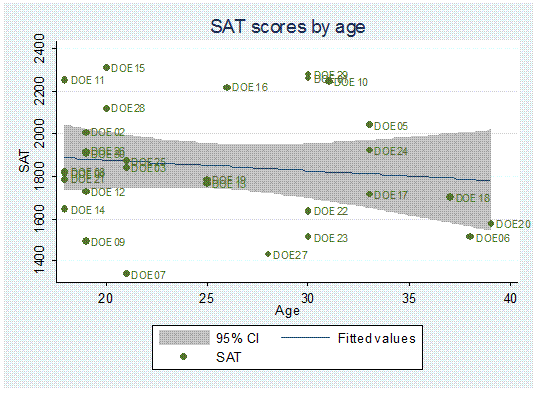
One problem in the graph is that some labels overlap making it difficult to read them.

We can rearrange them by moving them around the marker in a 12-hour clock position.

We need to create the variable position first. Type:

generate position=3

Position = 3 is the default, notice that all labels are to the right of the marker (3 pm).

We"ll move DOE29 to 12 o"clock and DOE10 to 6.

replace position=12 if lastname=="DOE29"

replace position=6 if lastname=="DOE10"

[IMPORTANT: If you get the message "(0 real changes made)" make sure you spell the names correctly, Stata is case-sensitive.]

To change the desired positions use the option mlabv()

twoway (lfitci sat age) || (scatter sat age, mlabel(lastname) mlabv(position)), title("SAT scores by age") ytitle("SAT")

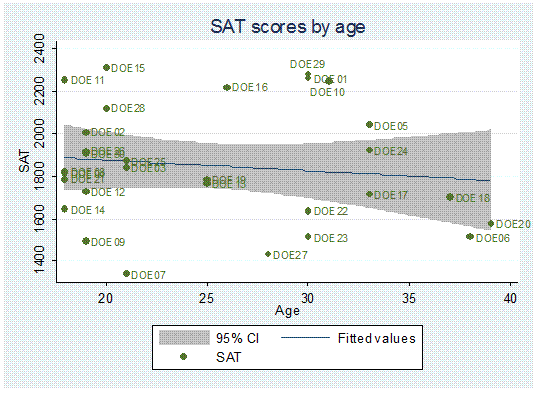
You may want to see if there is some kind of relationship by particular groups, let"s say by gender.

twoway scatter sat age, mlabel(lastname) by(gender, total)

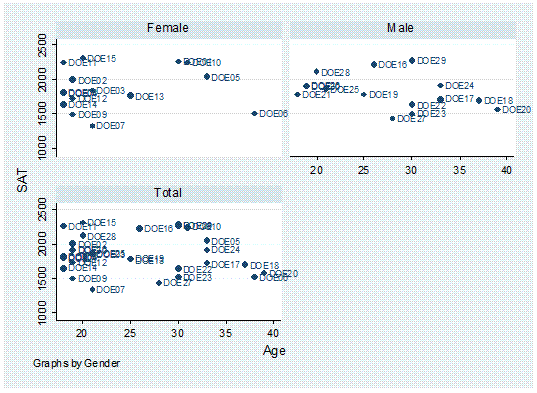
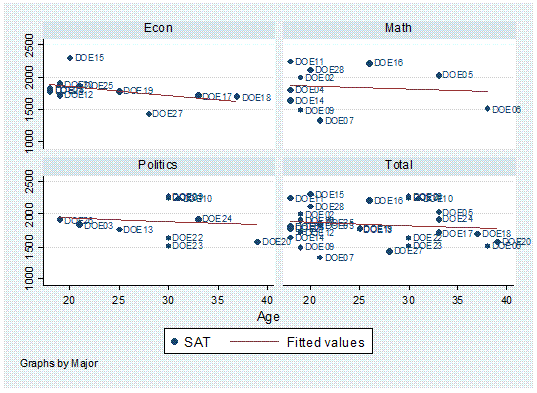
Or by major,

twoway scatter age sat, mlabel(lastname) by(major, total) || lfit age sat

Histogram

Histograms are another good way to visually explore data, especially to check for a normal distribution; here are some examples (type help histogram in the command window for further details):

histogram age, frequency

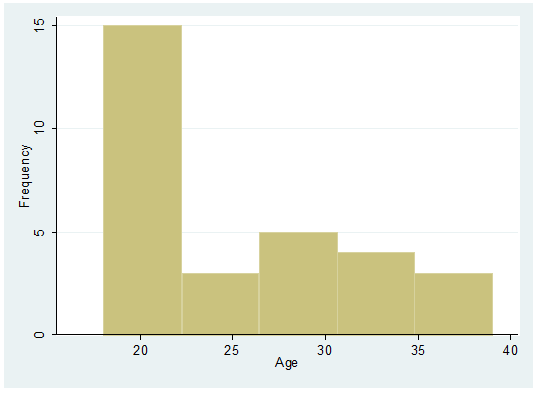
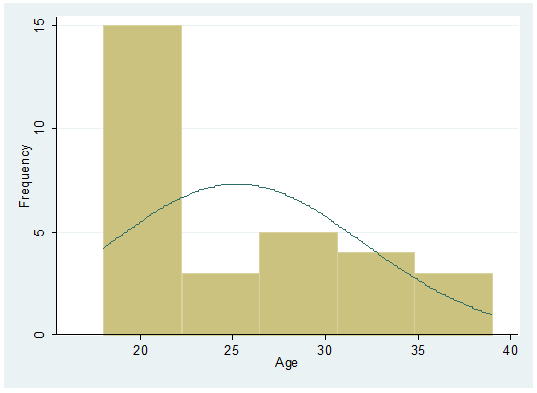
Adding a normal curve…

histogram age, frequency normal

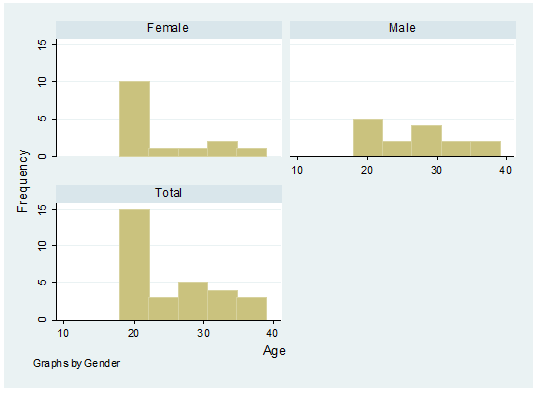
Age by gender

histogram age, frequency by(gender, total)

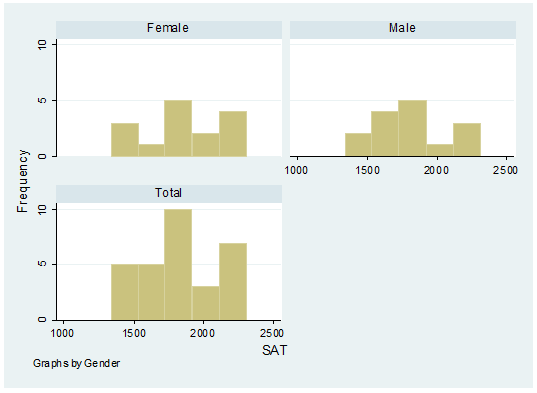
A histogram with SAT scores by gender.

histogram sat, frequency by(gender, total)

To save graph right-click on the graph, select "save graph" or you can also copy it to word by selecting "copy graph".

Bar chart

graph hbar (mean) age averagescoregrade newspaperreadershiptimeswk, over(gender) over( studentstatus, label(labsize(small))) blabel(bar) title("Student indicators")

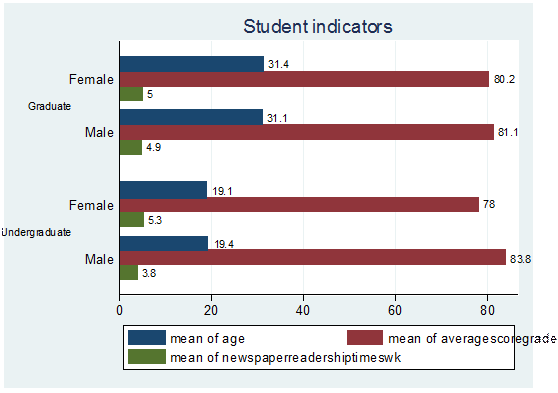
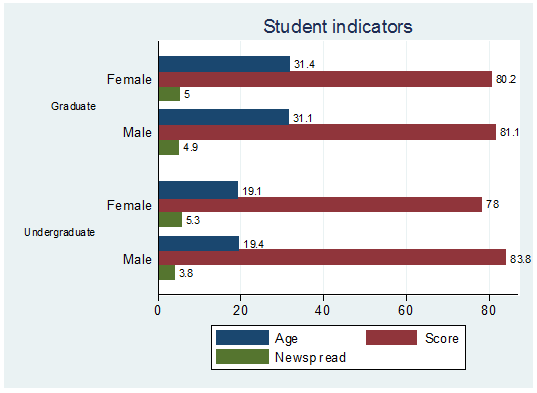
graph hbar (mean) age averagescoregrade newspaperreadershiptimeswk, over(gender) over(studentstatus, label(labsize(small))) blabel(bar) title(Student indicators) legend(label(1 "Age") label(2 "Score") label(3 "Newsp read"))

Graphing categorical data

To graph categorical data in Stata you will need a special program called catplot. If your version of Stata does not have it, you can install it by typing

ssc install catplot

Now type:

tab agegroup major, col row cell

To graph this table type:

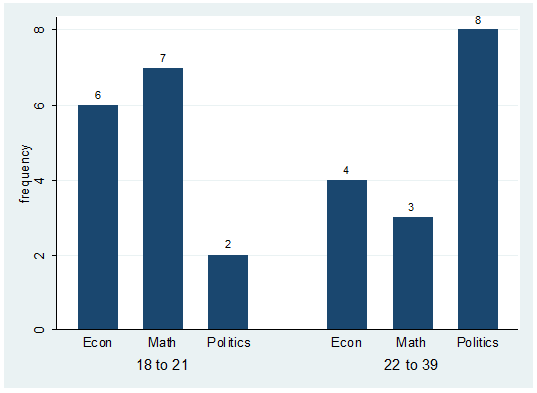
catplot bar major agegroup, blabel(bar)

This will get you the following:

Notice you may have to create the variable "agegroup" which is a recode of "age" where 1 "18 to 21" 2 "22 to 39".

The labels on the graph correspond to the number of students on each group. For example there are 6 students econ majors with ages between 18 to 21.

If you are interested on the percentages within "agregroup" you can specify this as follows:

catplot bar major agegroup, percent(agegroup) blabel(bar)

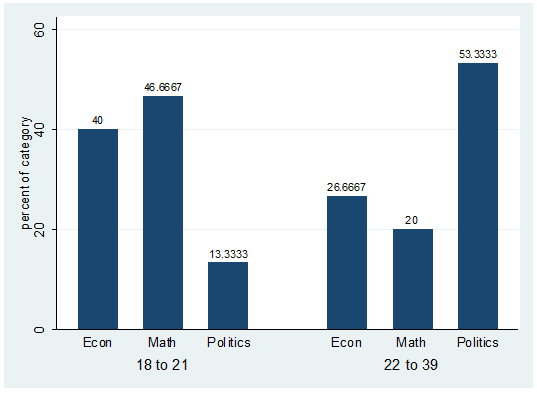
The percent() option indicates the reference group displayed in the graph. The labels on the previous graph correspond to the second row in the crosstab between agegroup and major.

If you are interested on the percentages within "major" you can specify this as follows:

catplot bar agegroup major, percent(major) blabel(bar)

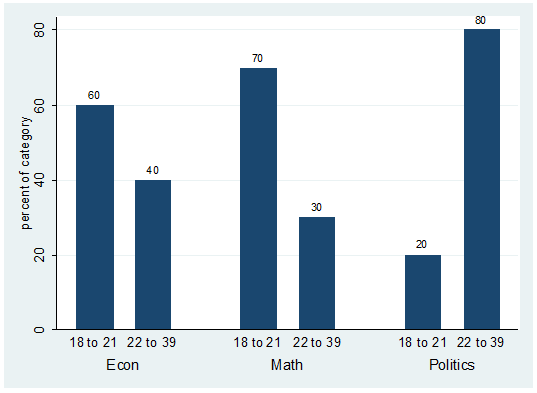
References and useful links

Hamilton, Lawrence C.Statistics with Stata (updated for Version 9). Brooks/Cole, 2006

Kachigan, Sam, Statistical analysis: an interdisciplinary introduction to univariate & multivariate methods. New York : Radius Press, c1986.

Textbook Examples. Regression with Graphics. by Lawrence Hamilton

http://www.ats.ucla.edu/stat/examples/rwg/

Stata Library. Graph Examples (may not work with STATA 10)

http://www.ats.ucla.edu/STAT/stata/library/GraphExamples/default.htm

DSS help-sheets for STATA

http://dss/online_help/stats_packages/stata/stata.htm

Introduction to Stata (PDF), Christopher F. Baum, Boston College, USA

A 67-page description of Stata, its key features and benefits, and other useful information.

http://fmwww.bc.edu/GStat/docs/StataIntro.pdf

STATA Corporation"s links to resources for learning STATA

http://stata.com/links/resources1.html

STATA FAQ website

http://stata.com/support/faqs/

Useful links to data, software and analysis

http://www.princeton.edu/~otorres/

UCLA Resources to learn and use STATA

http://www.ats.ucla.edu/stat/stata/

Graphs in Stata

http://data.princeton.edu/stata/Graphics.html