Bernoulli's Equation
Bernoulli's Equation
The Bernoulli
equation states that,
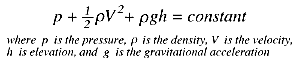
where
Although these restrictions sound severe, the Bernoulli equation is very useful, partly
because it is very simple to use and partly because it can give great
insight into the balance between pressure, velocity and elevation.
How useful is Bernoulli's equation? How restrictive are the
assumptions governing its use? Here we give some examples.
Pressure/velocity variation
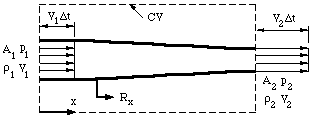
Consider the steady, flow of a constant density fluid
in a converging
duct, without losses due to friction (figure 14). The flow
therefore satisfies all the restrictions governing the use of Bernoulli's equation.
Upstream and downstream of the contraction we make the one-dimensional assumption that the
velocity is constant over the inlet and outlet areas and parallel.
 |
|
Figure 14. One-dimensional duct showing control volume.
|
When streamlines are parallel the pressure is constant
across them, except for hydrostatic head differences (if the pressure was higher in the middle of the duct, for example, we would expect the streamlines to diverge, and vice versa). If we ignore gravity, then the
pressures over the inlet and outlet areas are constant. Along a
streamline on the centerline, the Bernoulli equation and the
one-dimensional continuity equation give, respectively,
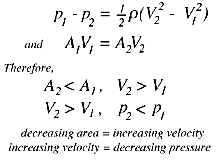
These two observations provide an intuitive guide for analyzing fluid flows, even when the
flow is not one-dimensional. For example, when fluid passes over a solid body, the
streamlines get closer together, the flow velocity increases, and the pressure
decreases. Airfoils are designed so that the flow over the top surface is faster than over
the bottom surface, and therefore the average pressure over the top surface is less than
the average pressure over the bottom surface, and a resultant force due to this pressure
difference is produced. This is the source of lift on an airfoil. Lift is defined as the
force acting on an airfoil due to its motion, in a direction normal to the direction of
motion. Likewise, drag on an airfoil is defined as the force acting on an airfoil due to
its motion, along the direction of motion.
An easy demonstration of the lift produced by an airstream requires a piece of
notebook paper and two books of about equal thickness. Place the books four to five inches
apart, and cover the gap with the paper. When you blow through the passage made by the
books and the paper, what do you see? Why?
Two more examples:
Example 1
A table tennis ball placed in a
vertical air jet becomes suspended in the jet, and it is very stable to small perturbations
in any direction. Push the ball down, and it springs back to its equilibrium position;
push it sideways, and it rapidly returns to its original position in the center of the jet.
In the vertical direction, the weight of the ball is balanced by a force due to pressure
differences: the pressure over the rear half of the sphere is lower than over the front
half because of losses that occur in the wake (large eddies form in the wake that dissipate
a lot of flow energy). To understand the balance of forces in the horizontal direction,
you need to know that the jet has its maximum velocity in the center, and the velocity of
the jet decreases towards its edges. The ball position is stable because if the ball
moves sideways, its outer side moves into a region of lower velocity and higher pressure,
whereas its inner side moves closer to the center where the velocity is higher and the
pressure is lower. The differences in pressure tend to move the ball back towards the
center.
Example 3
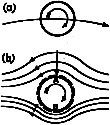
Suppose a ball is spinning clockwise as it travels through the air from left to right
The forces acting on the spinning ball would be the same if it
was placed in a stream of air moving from right to left, as
shown in figure 15.
 |
|
Figure 15. Spinning ball in an airflow.
|
A thin layer of air (a boundary layer) is forced to spin with the ball
because of viscous friction. At A the motion due to spin is opposite to that of the
air stream, and therefore near A there is a region of low velocity where the pressure
is close to atmospheric. At B, the direction of motion of the boundary layer is the
same as that of the external air stream, and since the velocities add, the pressure in
this region is below atmospheric. The ball experiences a force acting from A to B,
causing its path to curve. If the spin was counterclockwise, the path would
have the opposite curvature. The appearance of a side force on a spinning sphere or
cylinder is called the Magnus effect, and it well known
to all participants in ball sports, especially baseball, cricket and tennis players.
Stagnation pressure and dynamic pressure
Bernoulli's equation leads to some
interesting conclusions regarding the variation of pressure along a streamline.
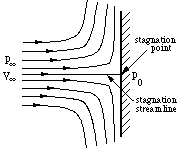
Consider a steady flow impinging on a perpendicular plate
(figure 16).
 |
|
Figure 16. Stagnation point flow.
|
There is one streamline that
divides the flow in half: above this streamline all the flow goes over the plate, and
below this streamline all the flow goes under the plate. Along this dividing streamline,
the fluid moves towards the plate. Since the flow cannot pass through the plate, the
fluid must come to rest at the point where it meets the plate. In other words, it
``stagnates.'' The fluid along the dividing, or ``stagnation streamline'' slows down
and eventually comes to rest without deflection at the stagnation point.
Bernoulli's equation along the stagnation streamline gives
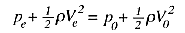
where the point e is far upstream and point
0 is at the stagnation point. Since
the velocity at the stagnation point is zero,
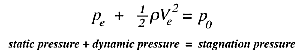
The stagnation or total pressure, p_0, is the
pressure measured at the point where the fluid comes to rest. It is the highest pressure
found anywhere in the flowfield, and it occurs at the stagnation point. It is the sum of
the static pressure
(p_0), and the dynamic pressure
measured far upstream. It is called
the dynamic pressure because it arises from the motion of the fluid.
The dynamic pressure is not really a pressure at all: it is simply a convenient name
for the quantity (half the density times the velocity squared), which represents the decrease
in the pressure due to the velocity of the fluid.
We can also express the pressure anywhere in the flow in the form of a
non-dimensional pressure coefficient
C_p, where
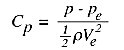
At the stagnation point C_p = 1, which is its maximum value. In the freestream, far from
the plate, C_p = 0.
Pitot tube
One of the most immediate applications of
Bernoulli's equation is in the measurement of velocity with a Pitot-tube. The Pitot
tube (named after the French scientist Pitot) is one of the simplest and most useful
instruments ever devised.
It simply consists of a tube bent at right angles (figure 17).
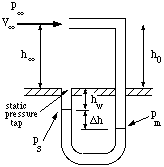 |
|
Figure 17. Pitot tube in a wind tunnel.
|
By pointing the tube directly
upstream into the flow and measuring the difference between the pressure sensed by the
Pitot tube and the pressure of the surrounding air flow, it can give a very accurate
measure of the velocity. In fact, it is probably the most accurate method available for
measuring flow velocity on a routine basis, and accuracies better than 1% are easily
possible. Bernoulli's equation along the streamline that
begins far upstream of the tube and comes to rest in the mouth of the Pitot tube
shows the Pitot tube measures the stagnation pressure in the flow.
Therefore, to find the velocity
V_e, we need to know the density of air, and the
pressure difference
(p_0 - p_e). The density can be found from standard tables if the temperature and
the pressure are known. The pressure difference
is usually found indirectly by using a ``static pressure tapping''
located on the wall of the wind tunnel, or on the
surface of the model.
Return to Aerodynamics of Bicycles Introduction.