Continuity Equation

When a fluid is in motion, it must move in such a way that mass is conserved. To see how mass conservation places restrictions on the velocity field, consider the steady flow of fluid through a duct (that is, the inlet and outlet flows do not vary with time). The inflow and outflow are one-dimensional, so that the velocity V and density \rho are constant over the area A (figure 14).

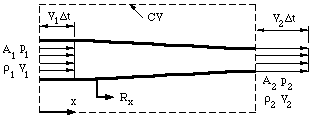Figure 14. One-dimensional duct showing control volume.

Now we apply the principle of mass conservation. Since there is no flow through the side walls of the duct, what mass comes in over A_1 goes out of A_2, (the flow is steady so that there is no mass accumulation). Over a short time interval \Delta t,

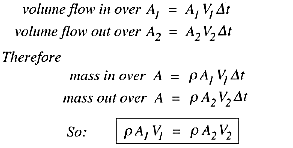
This is a statement of the principle of mass conservation for a steady, one-dimensional flow, with one inlet and one outlet. This equation is called the continuity equation for steady one-dimensional flow. For a steady flow through a control volume with many inlets and outlets, the net mass flow must be zero, where inflows are negative and outflows are positive.

Streamlines and Streamtubes

A streamline is a line that is tangential to the instantaneous velocity direction (velocity is a vector, and it has a magnitude and a direction). To visualize this in a flow, we could imagine the motion of a small marked element of fluid. For example, we could mark a drop of water with fluorescent dye and illuminate it using a laser so that it fluoresces. If we took a short exposure photograph as the drop moves according to the local velocity field (where the exposure needs to be short compared to the time it takes for the velocity to change appreciably), we would see a short streak, with a length V \Delta t, and with a direction tangential to the instantaneous velocity direction. If we mark many drops of water in this way, the streamlines in the flow will become visible. Since the velocity at any point in the flow has a single value (the flow cannot go in more than one direction at the same time), streamlines cannot cross. except at points where the velocity magnitude is zero, such as at a stagnation point.

There are other ways to make the flow visible. For example, we can trace out the path followed by our fluorescent drop using a long-exposure photograph. This line is called a pathline, and it is similar to what you see when you take a long-exposure photograph of car lights on a freeway at night. It is possible for pathlines to cross, as you can imagine from the freeway analogy: as a car changes lanes, the pathline traced out by its lights might cross another pathline traced out by an adjoining vehicle at a different time.

Another way to visualize flow patterns is by streaklines. A streakline is the line traced out by all the particles that passed through a particular point at some earlier time. For instance, if we issued fluorescent dye continuously from a fixed point, the dye makes up a streakline as it passes downstream. To continue the freeway analogy, it is the line made up of the lights on all the vehicles that passed through the same toll booth. If they all follow the same path (a steady flow), a single line results, but if they follow different paths (unsteady flow), it is possible for the line to cross over itself. In unsteady flow, streamlines, pathlines and streaklines are all different, but in steady flow, streamlines, pathlines and streaklines are identical.

Return to Aerodynamics of Bicycles Introduction.