FURTHER ILLUSTRATIONS OF THE BAYESIAN SOLUTION OF DUHEM'S PROBLEM

Abstract

1. The negligible effect of refutations in cases where most plausible rival theories are equally embarrassed by the observational result

 Dorling (1979) showed that, in spite of initial appearances to the contrary, if one inserts historically plausible assignments for scientists' subjective probability distributions over rival theories and auxiliary hypotheses, prior to their knowing the relations between the mathematical and observational results, their resulting changes in belief (and the absence of such changes) after discovering those relations, fall precisely in line with the dictates of rational probabilistic inference, both in the episode following Laplace's announced result and in that following Adams's announced result. In such an exercise it is necessary to insert one's best guesses as to the historically plausible initial data, without initial prejudice as to whether those will on calculation show that the scientists' subsequent reactions to the theory-observation conflict were or were not qualitatively the ones of ideally rational agents. But it is essential that the qualitative features of the results thus derived be reasonably "robust," that is to say reasonably stable under variations in the initial data within the range of one's uncertainties in assessing those initial data; those uncertainties are of course quite large when one gives a semi-quantitative interpretation to subjective probabilities, in a historical situation where one can at best guess how the scientists would have betted (had they been forced to do so), on the basis of their documentable qualitative assertions and one's feeling for the historical situation. It was clear to me from computations with slightly different figures, that the qualitative features of my results were appropriately robust, and the readers were invited to check this with their own best subjective estimates of the appropriate input data. However a closer analysis of the computation has now satisfied me that even I had underestimated the real robustness of my analysis, and that some features of the example which originally seemed to me likely to be essential to the production of such striking confirmation-refutation asymmetries are actually by no means essential at all. In particular I now see (a) that the quantitative precision of the predictions and observations is totally irrelevant to the numerical results and in fact factorizes out in the course of the analysis, (b) the asymmetry in the initial probabilities of the theory T and the auxiliary hypothesis H plays a much more minor role than I originally supposed: in fact one could reverse it and take H initially more probable than T, and though the effects would then be numerically less astounding, it would still be the case that the subjective probability of H would fall drastically after the refutation and that of T be little affected. It is really only the fact that the historical situation was one where virtually all serious rivals to T were equally embarrassed by the observational evidence, which determines that it is H and not T which has to be abandoned as a result of the conflict with the observations.
 
 

(a) The quantitative precision of predictions and observations is irrelevant to the asymmetric effect of refutations on theory and auxiliary hypothesis

          p'(T)     p(E|T)      p(T) 
(1)     -------- = --------- x ------- = 
         p'(~T)     p(E|~T)     p(~T)

          p(E|T&H)p(H) + p(E|T&~H)p(~H)       p(T)
      = --------------------------------- x --------
         p(E|~T&H)p(H) + p(E|~T&~H)p(~H)     p(~T)

 We now note that the first term in the numerator of the expression on the right vanishes if T&H entails ~E. Now I claim that all the other conditional probabilities in this expression are proportional to a common factor which measures the numerical precision of the result E. I took this factor to be 1/20 in my earlier analysis on the grounds that the result had to be accurate to 10% and its sign had to be correct. If I had taken it as 1/10 or as 1/5 or as 1/2 (the latter would correspond to merely predicting that there was an effect of the relevant order of magnitude and of the right sign), then this would simply have altered the total numerator and total denominator by the same factor, and hence made no difference to the final numerical result. How do I now justify this proportionality claim? Well p(E|T&~H) and p(E|~T&~ H) are now the probabilities of getting the observational result to the required order of accuracy on the assumption, inter alia, that there is an additional physical factor, whose expected presence or absence is independent of the choice between T and its rivals, which would substantially influence if not wholly account for the originally noted discrepancy between T and the observations. I therefore take both these probabilities as equal to the chance probability of 1/20 of meeting the specified precision criterion. For ~H here simply means that there is a further inadequately known causal factor which could be partly or wholly accounting for the original discrepancy with the observations.

 Now it is true that the base-line prediction might be different for some rival theories T' included in the disjunction of all rival theories which ~T represents, but in the presence of the noise-factor ~H, even a knowledge of such differences in base-line prediction would not enable us to predict more than that E fell within the right range, short of a quantitative theory of the unknown interfering cause represented by the falsity of H. So both these conditional probabilities reduce to the same chance probability of say 1/20.

 Now if we examine the remaining conditional probability p(E|~T&H), this is expandible as 1/p(~T) x 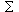 p(E|T'&H)p(T'), where the various T' include all logically possible rivals to T. Now I know that most of the serious alternatives to Newtonian theory in the mid-nineteenth century were just as embarrassed by the long-term speeding-up of the moon's motion as Newton's theory was. In fact quite generally in any theory with time-symmetric equations of motion (such as F = ma = some combination of functions of the distance; and this includes inter alia the rivals to Newton derived from a number of contact-action models of gravitational forces) there shouldn't be any such long-term speeding-up effects. Now it is true that one could imagine theories which would generate such long-term speeding-up effects, such as some aether theories, and theories with a finite velocity of propagation for gravitation, but in fact the difficulty with that class of theories is to avoid then producing an effect which is orders of magnitude too large, and hence totally irreconcilable with lunar and planetary observations. (Thus Laplace had shown e.g. that a certain attractive class of theories involving a time-asymmetric finite velocity of propagation for gravitation would indeed give such an effect but it would be vastly too large an effect unless this velocity were enormously larger than the velocity of light.) So all a theorist can do in this situation is to assign his own total subjective probability to the class of such theories as he would expect to be likely to produce a qualitative effect of this kind of the right order of magnitude. (My estimate of 1/50 here, i.e., about two percent of the rivals to Newton, is erring, I think, on the generaous side -- it is convenient to think of it as 2% of the rivals, though it is not based on a theory count, but on an estimate of the proportion of a typical mid-nineteenth century scientist's subjective probability distribution over rival theories and rival classes of theories to Newton's -- allowing of course for a certain proportion of this probability distribution being assigned to unknown rivals and classes of rivals). He must then multiply this figure by the chance of a theory that will just qualitatively do the job, actually doing it quantitatively correctly, i.e., by my earlier factor of, say, 1/20. This now establishes the result I claimed at the beginning of this paragraph, and we note that a smilar argument goes through for every case where a disconfirming experimental result E which is equally difficult to explain on the basis of the theoretically well-understood serious rivals to T, can be explained by an unknown physical influence (whose presence or absence is independent of the dispute between T and its rivals) seriously influencing the results. It follows that in such cases we can divide through by the numerical precision factor, read p(E|T&~H) and p(E|~ T&~H) as 1, and read p(E|~T&H) as the relative subjective probabilistic weight of those rivals T' to T which would deliver the goods quantitatively, or slightly less accurately as the proportion of rivals to T which would qualitatively produce such an effect as is observed.

 If I introduce the odds notation

 o(A:B) =def p(A)/p(B)
 
 

with the convention that I will drop the :B in the case that B = ~A [so I simply write o(T) for p(T)/p(~T), and o(H) for p(H)/p(~H)] then my formula (1) can now be conveniently rewritten in the form
 
 

                    1
(2) o'(T) = ------------------ x o(T)
             1 + o(T':~T)o(H)

(3) o'(H) = p(T') x o(H)

              1            100
o'(T) = --------------- = ----- x 9
              1     3      103
         1 + --- x ---
              50    2

(b) The initial symmetry of the probabilities of T and H is not the origin of the main asymmetry effect, and in fact plays a rather minor role in it.

The following initial observation is important here. The way we scale the probabilities is largely a matter of convention. We conventionally choose to scale them so that they fall between 0 and 1. This is most convenient for most purposes, but it does have some disadvantages. For example, it has the consequence that if a hypothesis starts with a probability of .95 and later evidence requires us to conclude that the subjective probability that it is false has tripled, p' then becomes .85, which does not look a very appreciable fall. However had we started with p = .75, and obtained similar unfavorable evidence p' would then become .25, which now looks a very appreciable fall indeed. Our conventional scale introduces a kind of psychological illusion here. In fact it is really the the probability of a hypothesis being true relative to the probability of its being false--the odds on the hypothesis, o in my notation --which is of most interest in discussions of confirmation and disconfirmation. This ranges between 0 and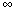  rather than between 0 and 1, and is just as good a measure of a person's degree of belief as the conventional probabilities. It is inconvenient in other contexts, but o and how it changes is the more appropriate object of attention here, and as we have seen it is easy to convert between o and the more conventional p. Therefore in discussing the symmetric effect of refutations I shall concentrate on the factors multiplying pr in formulae (1) and (2) so as not to be misled by what is partly a psychological illusion arising from an arbitrary convention. These factors are numerically 100/103 and 1/500 in the case I have so far computed.

 If we attend to formula (1) we see that the larger o(H) is, the larger is the denominator, and hence the greater the fall in o(T) to yield the later o'(T). So a low initial probability for H is an advantage from the point of view of saving the theory T. However H would hardly have been employed (implicitly) in the first instance had it been much less probable than 1/2, i.e., had o(H) been much less than 1. Only in peculiar and exceptional situations, e.g. when they can't calculate anything otherwise, do scientists consciously employ auxiliary hypotheses which they believe probably false. So the interesting cases are when o(H) is somewhere between 1 and 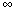 . Now we notice that with o(T':~T) = 1/50 in our example, o(H) could here be as large as 50, i.e., p(H) as large as about .98, and o'(T) could still only fall to a half of o(T), and even that may not look bad, owing to the psychological illusion created by the high initial value of p(T). Thus we take p(T) = .9 as before and take p(H) = .99, rather than equal to our original .6. The factor multiplying o(T) now becomes 50/149, a highly significant change, but when we do the computation and finally convert back into the p notation, we find p'(T) = .75, which doesn't look too bad a fall from p(T) = .9.

 If we now turn to look at the effect of p(T) in formula (3) for the changes of belief in H, at first it doesn't seem to appear at all, but it is nevertheless implicit, since p(T') = o(T':~T)x p(~T), hence the larger p(T) is the smaller p(~T) and the greater the fall in o(H) and hence in p(H). Conversely, the smaller p(T) is, the larger p(~T) and the smaller the fall in o(H) and in p(H). In fact in our examples p(T') is simply p(~T)/50. If we use this to compute p'(H) in the case when p(T) = .9 and p(H) = .99, we have already found p'(T) = .75, and we now find p'(H) = .165. In other words, starting with H much more probable than T, it is still H which bears the brunt of the refutation. Another interesting case to calculate is where we simply reverse our initial assignments to p(T) and p(H) and take now p(T) = .6, p(H) = .9. We find on computation p'(T) = .56, p'(H) = .067, a striking result which must surely conflict with the initial intuitions of most philosophers for such a case. It would be nice to illustrate this with a real scientific example. Indeed I think that for some mid-nineteenth century scientists my original example shopuld be reconstructed in just this way. Simply take a mid-nineteenth century scientist who was less sure than most that the Newtonian theory would prove correct to the relevant order of approximation for the prediction of the motions of the moon and the planets and who took more sriously than most the objectiion that effects like tidal friction could not plausibly be assumed to be quantitatively of the right order of magnitude. Indeed the question of whether a scientist ascribed a prior probability of .6 or .9 to T is not really an empirical question, but a question of how we explicate the scope of the theory T; p(H) is another matter altogether and in principle makes a true or false counterfactual claim about how a scientist would have betted, on my estimate it would have varied between scientists from a little below a half to about .99, all of which range is in agreement with the qualitative conclusions of my analysis.¹

 The important philosophical conclusion of this section is this: It is quite wrong to suppose that when a conjunction of hypotheses is refuted the most probable of them will in general suffer least, and the least probable of them in general suffer most. An exact probabilistic analysis shows that in general this is not so, and that far more relevant are the relevant sets of alternative hypotheses and how well they fare in the light of the observational evidence in question. It is the 1/50, the two-percent assigned as measure to the set of rivals of T which would qualitatively explain such a result without rejecting H, which is crucially responsible for the striking asymmetry of the effects of refutation on T and on H.
 
 

(c) The contrast with typical situations in the social sciences

2. Some examples of paradoxical confirmation by a "refuting" experiment

(2')    o'(T) = p(~H) x  o(T)
(3')    o'(H) = p(~T) x  o(H)

 However these formulas like formulas (2) and (3) are predicated on the assumption that p(E|T&~H) = p(E|~T&~H), i.e., the assumption that once the auxiliary conditions H, which permitted the deduction of the incorrect ~E in the first place, are dropped, there is no particular reason to suppose that T would then fare better or worse than its rivals in explaining or failing to explain the actual result E. Now the arguments which showed that this assumption was reasonable in the case-history of Dorling (1979) are rather generally applicable, that is to say they apply to all cases where once the particular auxiliary assumption H is dropped, the actual experimental result ceases to be particularly informative from a theoretical point of view, the conditions, which made a clear-cut experimental discrimination between the theory and its rivals possible, no longer being satisfied. However there are circumstances under which this assumption will break down. One is where the actual result E contains certain additional information, above and beyond mere falsity of the original theoretical prediction, which actually is discriminatory between T and its rivals. The philosophically exciting case here is where the actual result E, in spite of falsifying the original prediction from T, is easier to explain on the basis of T than on the basis of its rivals.Returning to formula (1) we then have, after some algebra,
 
 

                     p(E|T&~H)
(4) o'(T) = ---------------------------- x o(T)
             p(E|~T&~H) + p(E|~T&H)o(H)

 A typical illustration of this situation is provided when a theory makes a prediction which is quantitatively incorrect, but qualitatively correct, and where the quantitative discrepancy can be quite easily attributed to the presence of overlooked disturbing influences. Here o(H) is roughly 1 or not much larger, p(E|~T&H) is very small, and p(E|T&~H) is very substantially larger than p(E|~T&~H), so overall confirmation is still achieved. In spite of the quantitative failure of the original prediction from T, the rivals to T are embarrassed more than T is by the actual observational result. (Examples from the physical sciences are obvious. An example from the historical sciences would be where Marx predicts successfully an unlikely revolution and merely gets the date wrong.)

 A second similar case is where the original prediction is based on a rather long computation involving perhaps delicate mathematical or conceptual subtleties and where the quantitative failure of the prediction can easily be attrributed to some error in this computation, even when re-examination of the computation fails to identify what this error is. Here H is the assumption of a wholly error-free calculation and o(H) may be only about 9 even after the most meticulous re-examination; p(E|~T&H) -- now in fact independent of H -- may be very small, and p(E|T&~H) again much larger than p(E|~T&~ H) -- here equal to p(E|~T&H). So again we get confirmation of the theory in spite of failure of the original prediction.

 A somewhat more bizarre situation of this general kind arose in the case of the Einstein-de-Haas experiment which was designed to test a prediction based on the explanation of magnetism in terms of sub-microscopic circulating electric currents. The experiment gave the result expected except that it was wrong by a factor of 2. In this case the computation was so simple that there could hardly be anything wrong with it, and it was hardly possible to imagine any disturbing physical influence which could explain the experimental discrepancy. The quantitative discrepancy was therefore attributed to some unknown and wholly mysterious cause. Since H is the absence of this myserious cause, o(H) is here very large, certainly at least 1000. However, p(E|~T&H), the probability of getting the actual result in the absence of any mysterious extra cause and assuming that magnetism is not due to sub-microscopic circulating electric currents, is very small indeed, considerably less than one in a thousand. Since the presence or absence of this mysterious cause does not help ~T in explaning the observed result, p(E|~T&~H) is again correspondingly very small indeed. But p(E|T&~H) is now of the order of unity, so the overall result is highly confirmatory for this theory of magnetism and was accepted as such by physicists. (A mysterious effect of relativistic quantum mechanics later explained the missing factor 2.)
 
 

3. Paradoxical disconfirmation by experimental results which are too good to be true

                 p(E|T&~H)
(4) o'(T) = ------------------- x o(T)
             p(E|~T&~H) + o(H)

 However there is in fact an interesting class of cases where o(H) is less than 1, that is to say where the original prediction has been based partly on auxiliary assumptions which the theorists think are more likely to be false than true. For example a theorist might be able to make a clear-cut theoretical prediction only on the basis of the assumption that the accepted astronomical values for the masses of the planets and the parameters governing their motion are as accurate as the astronomers claim them to be, and he may himself think that this assumption is unlikely. In which case it may happen that a crucial experiment between T and its only major rival, precisely confirms the prediction of the rival theory T' but is nevertheless evidence for T and against T'. A case in point is the observed advance in the perihelion of Mercury conceived as a crucial experiment, not between Newtonian theory and General Relativity, but between the Brans-Dicke theory and General Relativity. Let Brans-Dicke be the theory T which predicts a result different by say -5 seconds of arc, from the 42-43 seconds of arc per century predicted by General Relativity and reported by the astronomers. Now Dicke argued that this difference between GR and the observation was, when intelligently and critically analyzed, really evidence for his theory and against GR. Dicke's argument was that the advance in the perihelion of Mercury was a small residual effect based on a complex astronomical calculation sensitive to the precise values of many other astronomical parameters, and that it was not believable that it would not have to be revised at some future date, as all similar supposedly accurately known numbers in astronomy hadc in the past undergone such revision, by amounts which would correspond in this case to several seconds of arc. Secondly he argued that there were specific possible disturbing effects ignored by the astronomers which suggested that the later revision was likely to be in the direction of the results predicted by his theory, the Brans-Dicke theory. He concluded, on my analysis correctly, that the exact agreement between GR and the currently officially accepted "observational" result, was in fact evidence, albeit weak evidence, for his theory and against General Relativity. (That the Brans-Dicke theory has had subsequently to be abandoned for other reasons -- the result of the lunar laser ranging experiments -- casts no reflection on the validity of Dicke's probabilistic reasoning here. In fact it remains the case that any scientist who is reasonably skeptical concerning the current claims of astronomers concerning the accuracy with which they know this particular figure, must regard the present very close agreement of General Relativity with that figure as a mild source of embarassment for GR, and as potentially favorable initial evidence for any rival theory which gave a prediction here a few seconds different from GR and the current "observational" result.)

 In all cases where in a straightforward crucial experiment. the prediction of one or other of the two theories is confirmed experimentally (this proviso is not trivial, sometimes the experiments confirm neither theory, or two or more apparently identical experiments give diametrically opposite results), then the probability of one theory must go up and that of the other go down, so every case where the formulae indicate that the apparently disconfirmed theory in fact increases its probability as a result of the experiment, will be a case where the other theory is made less probable as a result of getting its own right. It is therefore useful to look at such cases with the help of the corresponding Bayesian formula for confirmation: assuming p(E|T&H)=1, p(E|~T&H)=0
 
 

             o(H) + p(E|T&~H)
(5) o'(T) = ------------------ x o(T)   
                p(E|~T&~H)

 Another example might be the following (I don't know whether this is a real example, but it may be.) We know that ESP is a very delicate phenomenon very sensitive to psychological atmospheric conditions and so on, so not only must we do our experiments in a rigorously controlled situation which allows no possibility of cheating on the part of experimenters or subjects, but we must also optimalize the psychological conditions for the subject, having no skeptical persons in the environment, and so on. Suppose we do all this with a given subject in one of the best-controlled ESP setups in the world -- let us say at J. B. Rhine's laboratory at Duke University -- and suppose that the outcome of an experiment with a thousand playing cards is then the theoretically predicted one for the absolutely ideal conditions, namely the suibject guesses every single card precisely right! Now I, and I think every impartial judge, would regard such a result as totally discrediting the claims of the defenders of ESP. For let T be the claims of the defenders of ESP, and let H be the auxiliary hypopthesis which asserts both that cheating is effectively excluded and that the psychological conditions are ideal. Now clearly p(H), the prior probability that cheating is effectively excluded and that the psychological conditions are ideal, is less than the prior probability that the psychological conditions are ideal, and this must be exceedingly small, as every defender of ESP will admit. Secondly, according to the claims of the defenders of ESP, cheating is excluded in the best experiments of this sort, particularly in the experiments conducted at Rhine's laboratopry at Duke University, hence in evaluating p(E|T&~H), we need only evaluate the probability of E on the basis that the claims of the defenders of ESP are correct and that the psychological conditions are not ideal: hence p(E|T&~H) is virtually zero. Now ~T asserts that the claims of the defenders of ESP are false, and hence in consistency ~T must entail that there are very real opportunities for cheating on the part of subjects and/or experimenters in such experiments as those conducted at Duke University, so ~T already makes ~H highly probable and p(E|~T&~H) is essentially the probability of E if the claims of the defenders of ESP are false, and cheating has been a very real possibility. Hence p(E|~T&~H) is not particularly small at all, hence such an experimental result would very considerably reduce the probability of the claims of the defenders of ESP, and I think that the more sophisticated of ESP's defenders would agree with this analysis. For this reason I doubt that if such a result were ever obtained the experimenters would dare to publish it.

 These cases where a result which is too good to be true discredits the theory which yields it are relatively unusual. What more often happens is that that particular result is discredited but the probability of the theory is left where it was. That is to say, the assumption that p(E|T&H)=1, which underlies formula (5), is invalidated by this particular E, for which actually p(E|T&H) is practically 0. Formula (1) then yields (assuming, as in the derivation of (5), the "genuine crucial experiment" that p(E|~T&H)=0), approximately,
 
 

             p(E|T&~H)
(6) o'(T) = ------------ x o(T)
             p(E|~T&~H)

 A different kind of case where results "too good to be true" can discredit a theory, arises where the prediction of these results is based itself on a calculation, which while it may be the only one which can actually be carried out within the theory, ought not according to the theory to be accurate, or as accurate as the experiments seem to indicate. A classic case here seems to have been Dirac's calculation of the fine-structure spectrum of hydrogen from the Dirac equation, where he got agreement with experiment fater carrying out only a first-order calculation. He published this without going on to carry out the exact calculation, which was not especially difficult to do. one has the strong suspicion that Dirac himself suspected, on good general mathematical grounds, that the exact theory must give a different and therefore incorrect result, and that he therefore published while the going was good. As it happened Pauli carried out the exact calculation shortly afterwards and showed that, by a kind of unusual mathematical accident, it gave the same result asDirac's first-order calculation. So the theory was vindicated.

 In fact in the more recent history of quantum mechanics there have been a number of cases where "model" calculations have given far more detailed and precise agreement with experiment than anyone had any reason to expect, and such cases have constituted a major embarrassment for the theorists. I do not know whether there are still outstanding cases of this kind which have not yet been theoretically cleared up. In these cases we have from (1)
 
 

             p(E|T&H)p(H) + p(E|T&~H)p(~H)
(7) o'(T) = ------------------------------- x o(T)
                       p(E|~T&~H)

 A somewhat similar problem arises, perhaps, in relation to what have hitherto been almost universally regarded as the greatest successes of the quantum theory, namely the very precise correct predictions of the Lamb shift and of the anomalous magnetic moment of the electron, based on perturbation theory calculations. At first it seems that one obtains automatic confirmation here through a straight application of (1) in the form:
 
 

             p(E|T)
(8) o'(T) = --------- x o(T)  --where p(E|~T) << 1 = p(E|T)
             p(E|~T)

              p(E|T&H)p(H)              p(H)
(8') o'(T) = -------------- x o(T) = --------- x o(T)
                p(E|~T)               p(E|~T)

 But we now see that if this consideration concerning the value of p(E|~ T) is correct, then whether we get confirmation at all rather than disconfirmation here is highly sensitive to the value of p(H), that is to say to how close to 1 p(H) in fact is. It is also clear from our explication of H, above, thet the value of p(H) must invariably even fall, the further we carry these perturbation theory calculations. Furthermore p(E|~T) must rise asymptotically to 1, the further E is along the decimal places of the Lamb shift assuming tha all previous decimal places have been checked and shown agreement between the experiments and the perturbation theory calculations. Hence there must be some point at which the formula (8') will entail disconfirmatio rather than confirmation of the quantum theory by agreement of the results of perturbation theory calculations with the experimental value of the Lamb shift. The exciting question is have we already reached this point? I leave this to the mathematicians, since it depends on their hunches as to the probability of H. If they say p(H) is not more than .9, then we have already reached this point; if they say p(H) is .99 we are tottering on the brink of it; if they say p(H) is .999 or more, then we probably have some way to go. The opinions over H in the literature seem to range from outright skepticism on purely mathematical grounds to enormous confidence on supposedly empirical grounds, sometimes both views being expressed by the same author. But such confidence on empirical grounds would be, in the present context, just a logical muddle.
 
 

4. How to draw the right asymmetric conclusions from two crucial experiments with directly conflicting results

 In the solar eclipse experiments of 1919, the telescopic observations were made in two locations, but only in one location was the weather good enough to obtain easily interpretable results. Here, at Sobral, there were two telescopes: one, the one we hear about, confirmed Einstein; the other, in fact the slightly larger one, confirmed Newton. Conclusion: Einstein was vindicated, and the results with the larger telescope were rejected.

 Let T be general relativity and N be Newton's theory (or for the sophisticated reader who appreciates that Newton's theory was already refuted by the experiments confirming Special Relativity and was therefore here a non-starter, let N be Nordströ m's theory which was still a serious rival and predicted no light-bending effect of the sun). Let H be the hypothesis that both telescopes worked as they were expected to. Then we have:
 
 

               p(E|T&H)p(H) + p(E|T&~H)p(~H)
(9) o'(T:N) = ------------------------------- x o(T:N)
               p(E|N&H)p(H) + p(E|N&~H)p(~H)

                p(E|T&~H)
(9') o'(T:N) = ----------- x o(T:N)
                p(E|N&~H)

 The case of the celebrated tests of the Bell-inequality which was predicted to be satisfied if any local hidden variable theory, and to be violated if the quantum theory, were correct, is somewhat similar, but also brings out interesting and somewhat startling additional features. I will restrict myself to the experiments of Holt and Clauser. Here we had two experiments which differed in a number of minor but theoretically relevant details. Holt's experiments were conducted first and confirmed the predictions of the local hidden variable theories and refuted those of the quantum theory. Clauser's results a little later confirmed the predictions of quantum theory. Clauser examined Holt's apparatus and could find nothing wrong with it, and obtained the same results as Holt with Holt's apparatus. Holt refrained from publishing his results, but Clauser published his, and they were rightly taken as excellent evidence for the quantum theory and against hidden-variable theories. In order to make the situation as paradoxical as possible I shall make the following assumptions (which I suspect to be not far from the truth). (a) That Clauser and Holt both hoped to refute the quantum theory and that both initially thought that the predictions of then local hidden variable theories were more likely to be correct here than those of the quantum theory. (b) That Clauser and Holt both had initially more confidence in Holt's apparatus than in Clauser's. (c) That even tentative preliminary results with Clauser's apparatus marginally favouring the quantum theory coming after much more definitive results from Holt's, in the other direction, were nevertheless enough to convince both experimenters that the quantum theory was correct and that there was some unexplained fault in Holt's experimental design.

 Let us consider the result of Holt's experiment. We apply
 
 

              p(E|T&H)p(H) + p(E|T&~H)p(~H)
(10)o'(T) = --------------------------------- x o(T)
             p(E|~T&H)p(H) + p(E|~T&~H)p(~H)

                  .2  
(10') o'(T) = ---------- x o(T)
               .8 + .2

               p(E|T&H)p(T) + p(E|~T&H)p(~T)
(11) o'(H) = --------------------------------- x o(H)
              p(E|T&~H)p(T) + p(E|~T&~H)p(~T)

          .55
     = ---------- x 4 = 2.2
       .45 + .55

Now Clauser does his experiment, with a set-up differing in theoretically irrelevant details from Holt's, but let us suppose that Clauser only sets p(H) with H relating to his set-up, as .5, i.e. let us suppose that both experimenters have more confidence in Holt's apparatus than in Clauser's less-tried set-up. Suppose Clauser obtains initial results which significantly confirm the correlations predicted by the quantum theory, but not overwhelmingly so. Say there is still a 1% chance that the apparent correlations are produced by mere chance fluctuations. Then formula (10) yields:
 
 

         1x.5 + .01x.5
o'(T) = ---------------- x o(T) = 50.5 x o(T)
        .01x.5 + .01x.5

 What influence has the result had on our relative confidence in Clauser's and Holt's experimental set-ups? Applying formula (11) to Clauser's apparatus and result, we obtain
 
 

         1x.14 + .01x.86
o'(H) = ------------------ x 1 = 15
        .01x.14 + .01x.86

 We therefore have here another interesting case of asymmetry, where two essentially similar experiments are done and where the conditions are nevertheless such that the asymmetry acts in precisely the opposite direction to what one might expect from the experimenters' initial theoretical prejudices, their relative initial confidences in their apparati, and the relative tentativeness of their results from those apparati.
 
 

5. Conclusions

 It appears that in the past even many experts have sometimes been misled in trickier reasoning situations of this kind. A more widespread understanding of the adequacy and power of the kinds of Bayesian analyses illustrated in this paper could prevent such mistakes in the future and could form a useful part of standard scientific education. It would be an exaggeration to say that it would offer a wholly new level of precision to informal scientific reasoning, for of course the quantitative subjective probability assignments in such calculations are merely representative surrogates for informal qualitative judgments. Nevertheless the qualitative conclusions which can be extracted from these relatively arbitraty quantitative illustrations and calculations seem acceptably robust under the relevant latitudes in those quantitative assignments. Hence if we seek to avoid qualitative errors in our informal reasoning in such scientific contexts, such illustrative quantitative analyses are an exceptionally useful tool for ensuring this, as well as for making explicit the logical basis for those qualitative conclusions which follow correctly from our premises, but which are sometimes nevertheless surprising and superficially paradoxical.
 
 

Notes

2 Freud's invocation of repression here, represented in my notation by ~ H, involves on the face of it a p(~H) which fails to satisfy the independence condition that p(T&~H) = p(T)p(~H). However it is possible in principle to specify independently of Freud's theory the objective conditions under which it would here predict repression, namely the objective circumstances under which Freud's theory would predict that sexually enlightened members of Freud's circle, anxious to hold nothing back which would be relevant to the cure of their child would be unable consciouisly to admit the fact that they had ever attempted sexual intercourse a tergo in the upright position, and that sleeping arrangements could ever have been such that Hans could have witnessed their intercourse, let alone in a position which they claimed never to have contemplated as likely to be conducive to satisfaction. Ultimately the predictions of Freud's theory here, including ones yielded with small probabilities, involving combinations of repressions whose joint probability mist inevitably be much lower than their individual probabilities, must yield probabilistic predictions of people's observable and other behaviour based on theory independent information concerning their past experiences. Otherwise no empirical evidence can be in any way relevant to the theory. Hence it must in principle be possible here to reconstrue H and ~H, in such a way that they state theory independent necessary conditions, so that the independence assuption employed in my present analysis becomes applicable. We are not seeking numerical precision here, but we are interested in whether the negative evidence from the parents' assertions reduces the probability of Freud's dream analysis being correct by 1/5, 1/20, or 1/100. It is ultimately a question of assessing Freud's own expectations, prior to quizzing the parents, of what they would be prepared, without undue brainwashing, to admit on reflection, in the interests of curing their child. Of course it is also possible to carry through my analysis without the independence assumption, at the cost of further complexity in formulas (2) and (3). (go back)

3 In spite of published results to the contrary, there is still a persistent misunderstanding in the literature (perpetuated in the recent book of Horwich) to the effect that Bayesian Conditionalization is a sort of optional extra requirement added by some proponents of subjective probability, but that it is not rationally de rigeur, and unlike the other axioms has no justification on the basis of Dutch book arguments. In fact the situation is that Bayesian conditionalization is strictly de rigeur and that one can by means of Dutch books systematically make money off anyone who departs in any systematic way from Bayesian Conditionalization. Since the general proof (due to Putnam and David Lewis and published by Teller) seems to have convinced none of the sceptics (partly because Teller himself expressed reservations concerning it), it seems pointless repeating it here. What I shall do instead is to describe a typical example of how one can make a Dutch book against a scientist who refuses to modify his systematic beliefs in the light of evidence in accordance with Bayesian conditionalization, and then subsequently indicate how that example can be generalized.

 Suppose that Tycho Brahe, believing initially that his own theory is twice as probable as that of Copernicus, and assigning a negligible probability to all other contenders, hears that preliminary observations with the new Dutch telescope have indicated the presence of what appear to be mountains on the moon. Now the more detailed appearance of these mountains is important for the theoretical dispute between Tycho and the Copernicans, since Tycho expects these mountains to appear tilted in relation to the moon's motion through space, whereas the Copernicans expect them to appear oriented perpendicular to the surface of the moon, just as the earth's mountains are oriented apparently perpendicular to its surface, in spite of the rapid rotation and the even more rapid translatory motion assigned to the earth by the Copernicans. Let T be the theory of Tycho, C the theory of Copernicus, and E the possible future more refined telescopic observation that the mountains on the moon indeed appear oriented perpendicularly in relation to its surface. Now p(E|C) = p(E|~T) = approximately 1, since Copernicanism is incompatible with the proposition that physical motion through space could produce such marked physical effects as a tilting of the moon's montains in relation to the moon's motion through space. p(E|T) is not zero, since Tycho certainly has other arguments for a stationary earth than the orientation of the earth's mountains, and T is perfectly compatible with the absence of such gross physical effects of motion through space. Let us suppose that Tycho cautiously sets p(E|T) as high as 1/4: such an appearance of the moon's montains is thus unexpected in Tycho's theory, but not all that remarkable. Now let us suppose that a better telescope has been designed which is agreed will settle the question of the truth or falsity of E. For Tycho p(E&T) = p(E|T)p(T) = 1/4 x 2/3 = 1/6. This means that he is in principle prepared to offer us odds of 5:1 against both E and his theory T being simultaneously true. Let us suppose we take him up on this and bet him $100 that both E and T are true. Now for Tycho p(E) = p(E|T)p(T) + p(E|C)p(C) = (1/4)(2/3) + 1x(1/3) = 1/2. This means that he is in principle prepared to offer us even odds on the truth of E. Let us suppose we take him up on this too and bet him $200 against the truth of E.

Suppose the new telescopic observation is then carried out. If E turns out to be false, we lose $100 to Tycho on our first bet, and win $200 from him on our second bet, so we win $100 from him overall. If E turns out to be true, Tycho wins $200 from us on the basis of the second bet but the first bet is still outstanding. If he were a rational Bayesian he would also have to take p'(T) = p(E|T)p(T)/p(E) = (1/6)/(1/2) = 1/3, i.e., he will have to admit that it has now become twice as likely that Copernicanism is true than that his own theory is true. But suppose he is a bigoted non-Bayesian, refuses to modify his prior beliefs in accordance with Bayesian conditionalization, (believing himself justified in this stance on the authority of Hacking, Hesse, Gillies, Levi, Kyburg, and Horwich), and simply keeps p(T) unchanged at 2/3. And suppose that we knew in advance that this would be his reaction, should E turn out to be observed, either on the basis of general observations of his character, or on the basis of his explicit philosophical repudiation of Bayesian conditionalization as rationally obligatory in this situation, and that this was indeed our motivation for placing our original bets in the way we did. Now p'(T) = p(T) = 2/3 means that he is prepared to offer us odds of 2:1 against his theory being false. Let us then take him up on this and bet him $200 at these odds that T is in fact false.

 Now what is the final reckoning? If E turns out to be false we win, as we have already seen, $100 overall from Tycho. If E turns out to be true and T true, we win $500 from the first bet, but lose $200 from the second bet, and lose $200 from the third bet, so we again win $100 overall from Tycho. If E turns out to be true and T false, we lose $100 from the first bet, lose $200 from the second bet, but win $400 from the third bet, so we again win $100 overall from Tycho. So with this system of bets we win $100 and Tycho loses $100 no matter what happens. We have made a Dutch book against Tycho.

 Now there are a number of idealizations in this example which I shall presently show are inessential. But the essential point is this. Whenever one knows in advance, that a scientist will, in a certain eventuality, change or fail to change his beliefs in a manner which violates Bayesian conditionalization, and one knows precisely in what way he will then violate it, one can take advantage of this knowledge and place bets with him in such a way as to be absolutely sure of winning money off him, whether or not this eventuality arises. In our particular illustration we assumed that we knew in advance that Tycho would, if E did turn out to be observed, then modify his belief in his theory less than is rationally required by Bayesian conditionalization. That is why our initial bet was placed in favour of T&E and out third bet -- only subsequently placed if E turned out in fact true -- was placed against T. Had instead we known in advance that Tycho would depart from Bayesian conditionalization in the opposite direction, i.e., by over-reacting, rather than under-reacting to the eventuality of unfavourable evidence, then we would have begun differently and placed our initial bet in favour of ~T&E and our final bet in against T at Tycho's later odds in the eventuality of E being verified. We would equally have achieved a Dutch book, with an appropriate choice of stakes.

 The argument is simplest if one knows in advance both the magnitude and the direction of departure from Bayesian conditionalization to be anticipated from a given non-Bayesian scientist in a certain eventuality. If one knows only the direction of departure to be anticipated, then in general one can only set up a weaker form of Dutch book, namely one where we can either win or break even, and the non-Bayesian scientist can either lose or break even. Not perhaps quite as satisfying, but just as embarrassing a situation for the non-Bayesian. Indeed more generally it is sufficient for us to know that the given non-Bayesian scientist will on average depart from Bayesian conditionalization in a predictable direction, for us to be able to make bets with him so as to be sure on average of making money off him. (There is no recipe I know of for systematically bankrupting a scientist who departs erratically from Bayesian conditionalization in a wholly random and unpredictable manner, but nevertheless conforms to Bayesian conditionalization on average. But this is hardly a strategy that any non-Bayesian philosopher would recommend. I suspect that a more ingenious betting strategy, including e.g. bets on the directions of individual departures, could systematically bankrupt even this scientist, but I have not examined this possibility in detail.)

 One idealization in the example given, is that I have assumed the legitimacy of bets for and against the theory T, which is tantamount to assuming that Tycho could foresee future possible crucial experiments which could in principle settle such bets. In fact all that is necessary here is the existence of forseeable future experiments some of whose possible results would have differing conditional probabilities relative to the theories T and C, e.g. observations suggesting a solar rotation, attempts to measure a possible oblateness of the earth, or variation of gravity with latitude, observations on the trade winds, attempts to observe stellar parallax, etc. The whole argument can be recast if necessary in terms of bets not on the truth of E&T and on the truth of T, but on the truth of E&E' and on the truth of E', where E'is such a theoretically relevant future possible observational result. How Tycho will react, or fail to react, to the possible result E, will affect the relation between the initial and subsequent probabilities he assigns to E&E' and to E', and with a little more patience and a little more algebra, analogous Dutch books can be constructed where all bets relate to such clearly decidable propositions, and with the effect that Tycho must lose money however the actual later results turn out, even where the future results are far from crucial but merel suggestive in relation to the dispute between Tycho and the Copernicans. (It goes without saying that these systems of bets depend in no way for their success on the assumption that the later evidence will favour Copernicus rather than Tycho.)

 A second idealization in the example, is the assumption that Tycho is prepared to enter into bets at precisely the odds which correspond to his own subjective probability assignments. This assumption is unnecessary in the example. It is sufficient that he be prepared to enter into bets at odds close to these, but in every case slightly more favorable to him, in the sense that for every bet which he enters into, he associates with it, at the time, a positive expected monetary gai for himself. The Dutch book argument still works against him under these conditions. One can fix the odds and stakes, e.g., in such a way that Tycho only enters into a bet if, at the time, he obtains, by entering into it, on his own estimation, an expected monetary gain for himself of at least a dollar: we can still ensure by choosing our stakes appropriately a certain loss of $100 for Tycho, overall, no matter what happens.

 It is of course a fundamental assumption that Tycho is in principle prepared to cash his verbal claims about his own subjective probabilities in terms of a willingness to enter into actual monetary bets. Strictly speaking we should allow here for the non-linearity of his likely money-utility curve, for disutilities associated with risk-avoidance and so on, but this merely complicates the calculation and alters nothing essential. All that is essential is that he is prepared to put his money where his mouth is, that his verbal claims about his beliefs and expectations are not contradicted by his unwillingness to behave in accordance with them, when it comes to the crunch.

 Quite apart from this purely financial justification of it rationality (only by conforming to Bayesian conditionalization can we avoid being systematically bankrupted by an intelligent Bayesian with no more priviledged access to the future than we have), Bayesian conditionalization can in principle be reduced to the following rationality requirement, which is already implicit in the philosophy of Sir Karl Popper: If two hypotheses both entail E, and we subsequently discover that E is true and that is all we discover, then this discovery alone should in no way alter our relative preference between these two hypotheses. Proof: formula (1) can be proved by taking E&T as one of these hypotheses E&~T as the other, and observing that since p'(E) = 1, p'(T) = p'(E&T) and p'(-T) = p'(E&~T), so all that (1) maintains (ignoring the simplified expansion on the right which is here irrelevant) is that p'(E&T)/p'(E&~T) = p(E&T)/p(E&~T). Q.E.D. In other words, changing one's mind for no good reason is irrational, while intending systematically to change one's mind for no good reason is to invite financial ruin, and to opt out of the rational scientific enterprise. Bayesian conditionalization is not an optional rule of inference but a minimal consistency requirement, a sine qua non for rational inference in experimental science, in applied statistics, in general epistemology, in the deliberation of jurors, and in most common sense reasoning in everyday life. (go back)

References

 Gillies

 Hacking, I.

 Hesse, M.

 Horwich, P. (1982) Probability and Evidence, Cambridge University Press

 Kyburg, H.

 Levi, I.

 Teller, P. (1973) "Conditionalization and observation", Synthese26, 218-258.

 Putnam, H. (1963) "Probability and Confirmation", The Voice of America, Forum Philosophy of Science, 10, U. S. Information Agency. Reprinted in Mathematics, Matter and Method, Cambridge University Press, 1975, pp. 293-304.
 
 

[Ed.'s Note: Bibliographical information is incomplete. It will be available shortly]