Confidence intervals for the mean

Another way to express how close the realization of the experimental-result average is to the expected value E[R] is through confidence intervals for the mean.

Let denote the probability that the outcome of lies within a certain interval centered at the true value:

 

After the experiments have been performed, the value a can be replaced

by a fraction of , the realization of :

 

Assuming the sample mean is normally distributed, eqn. (10) can be written as:

 

which leads to:

 

with  - the cumulative standard normal distribution. Data indicate that various soil properties are, with reasonable accuracy, normally distributed [9], so that the assumption of normality for their sample average is a fortiori justified.

The solution (12) is only valid if the standard deviation of the test results is known, which in general is not the case. By replacing by its estimate - the sample standard deviation  - the expression 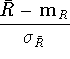in eqn. (11) is approximated by 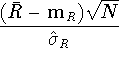, which follows a Student's t distribution with N-1 degrees of freedom [5] Denoting by the respective cumulative distribution and taking advantage of its symmetry, the probability in (10) can be evaluated as:

 

It is important to observe that, if the bias is ignored or negligible, the reliability of experimental results very much depends on the number of tests performed: for a certain series of experiments, with given and for a given interval size , one can increase the level of confidence (or decrease the expected error ) as much as needed, at the expense of additional tests.