A second comparison index is proposed to account for the influence that
the quality of the experimental results has on the
reliability to be assessed to the
"class A" predictions.
The index is based on the measure of the half length "b" of
the confidence interval centered at the predicted value "p" which
contains the estimated true mean value " ![]() " of the experiment
with the probability
" of the experiment
with the probability ![]() .
In other words,
.
In other words,
![]() is the likelihood that the true
value
is the likelihood that the true
value ![]() lies within the confidence interval of length 2b,
centered at the predicted value p:
lies within the confidence interval of length 2b,
centered at the predicted value p:
This "b" index can only be evaluated when more than one experimental result is available for comparisons with "class A" predictions. The methodology is briefly described in the followings.
Before a series of N experiments are performed, their results
![]() are random variables with expected values
are random variables with expected values ![]() and standard deviations
and standard deviations ![]() ,
, ![]() .
The following assumptions are made:
.
The following assumptions are made:
Under the above assumptions, the results ![]() are identically distributed
random variables, i.e.
are identically distributed
random variables, i.e. ![]() , for
all
, for
all ![]() (assumption 1), the expected outcome equals the
true value,
(assumption 1), the expected outcome equals the
true value, ![]() (assumption 2), and the average
outcome
(assumption 2), and the average
outcome 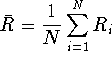 is a normally distributed random variable, even for small N
(assumption 3).
The mean and standard deviation of
is a normally distributed random variable, even for small N
(assumption 3).
The mean and standard deviation of ![]() are
[12]:
are
[12]:
![]() and
and
![]() , respectively.
It follows that the random variable:
, respectively.
It follows that the random variable:
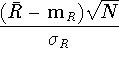 is standard normal.
Since the real standard deviation of the test results is not known,
it is replaced by its estimate - the sample standard
deviation
is standard normal.
Since the real standard deviation of the test results is not known,
it is replaced by its estimate - the sample standard
deviation ![]() , evaluated after the experiments have been
performed.
The new random variable:
, evaluated after the experiments have been
performed.
The new random variable:
can be shown to follow a Student's t distribution with N - 1 degrees
of freedom [12].
Denoting by ![]() the respective cumulative distribution, and
replacing
the respective cumulative distribution, and
replacing ![]() in (5) using (6), one gets:
in (5) using (6), one gets:
with:
After the experiments have been performed and the results ![]() -
realizations of
-
realizations of ![]() - are known at every time instant t,
the random variable
- are known at every time instant t,
the random variable ![]() in (8) is replaced by its realization
in (8) is replaced by its realization
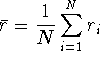 ,
and, given a value for
,
and, given a value for ![]() ,
the equation (7) can be numerically solved for
,
the equation (7) can be numerically solved for ![]() .
.
The meaning of the size b of the ![]() confidence interval is illustrated
in the above figure.
Before the experiments are performed, the random variable
confidence interval is illustrated
in the above figure.
Before the experiments are performed, the random variable ![]() has
the probability distribution function
has
the probability distribution function ![]() , shown in
the figure.
If the standard deviation of the test results
, shown in
the figure.
If the standard deviation of the test results ![]() is known,
is known,
![]() is derived from the normal distribution, and it comes
from the Student's t distribution if
is derived from the normal distribution, and it comes
from the Student's t distribution if ![]() is
approximated by the sample standard deviation
is
approximated by the sample standard deviation ![]() .
After the experiments,
.
After the experiments, ![]() is replaced by its realization
is replaced by its realization ![]() ,
but the true value
,
but the true value ![]() remains unknown.
Under the "random sampling" assumption, the uncertainty in locating
the true value
remains unknown.
Under the "random sampling" assumption, the uncertainty in locating
the true value ![]() relative to
relative to ![]() can be expressed
by the same probability distribution function.
Finally, given the predicted value p, the
can be expressed
by the same probability distribution function.
Finally, given the predicted value p, the ![]() confidence interval
has a size 2b, corresponding to an area which equals the
likelihood
confidence interval
has a size 2b, corresponding to an area which equals the
likelihood ![]() (hatched area).
(hatched area).
An overall measure of how close the predicted time history is to the
experimental measurements is obtained by averaging the value ![]() ,
computed at every time instant t, over the analysis time interval
,
computed at every time instant t, over the analysis time interval
![]() .
Finally, to get a nondimensional index, the average value is normalized with
respect to the initial effective vertical stress
.
Finally, to get a nondimensional index, the average value is normalized with
respect to the initial effective vertical stress ![]() :
:
The quantity ![]() , evaluated for a certain
, evaluated for a certain ![]() value,
will be
refered to as "size of
value,
will be
refered to as "size of ![]() confidence interval".
confidence interval".