Chapter 2 Experimental

2.1. Helium Atom Reflectivity

The majority of the experiments performed in this thesis have utilized helium atom reflectivity (HAR) to continuously monitor surface adsorbate populations and to observe adsorption and desorption behavior in real-time. Oftentimes referred to as thermal energy atom scattering (TEAS), this technique offers extremely high sensitivity with low risk for damage to the monolayer.

When probed with a collimated helium beam, a close­packed metal surface behaves like a mirror. If the single-crystal surface is clean and well­annealed, the specular reflection signal will be quite strong, indicating a high degree of order. However, if the surface is contaminated with adsorbates or contains defects, the reflection signal will be less intense. Thus, a decay in the intensity of the specular reflection signal is observed when the clean crystal surface is covered with adsorbates (Figure 2-1).

In principle, when enough molecules have adsorbed to complete a monolayer, the return of order may cause the specular signal to recover. However, the likely presence of structural defects in the organic monolayer, the much larger molecular corrugation of the adlayer, as well as the higher probability of inelastic collisions, will make the specularity of the completed overlayer significantly less than that for the clean metal surface.

Since the loss of specular intensity results from any event which causes diffusive scattering, attractive interactions with adsorbate molecules at distances more than twice their repulsive diameters are sufficient to deflect the helium atoms away from the specular direction. Typically, this response can be seen experimentally in effective adsorbate cross­sections at low coverage that are many times larger than their expected hard­sphere cross-sections.

Figure 2-1. Angular distribution of scattered helium from Au(111) at 250 K. Clean crystal (-) shows high degree of specularity while decane covered crystal (- - -) shows "cosine distribution" due to highly inelastic scattering.

As the coverage increases, the overlap of the scattering cross-sections of the individual adsorbates will affect the rate of specular decay provided by each additional adsorbate molecule. Depending on the ordering mechanism, the resulting normalized specular decay (I / I_o) will be a linear, polynomial, or exponential function of increasing coverage (), monolayer density (n_s), and the scattering cross-section of the adsorbate at the limit of zero coverage () (Table 2-1).

For molecules that adsorb at random locations, the likelihood of random overlap also increases with coverage thus reducing the effective cross-section. If the molecules do not adsorb completely randomly but instead are constrained to adsorb preferentially on substrate lattice sites ("lattice gas"), the increased spacing of adsorbates will limit the degree of overlap possible and a slower decay of effective cross-section will be observed. In contrast, adsorbate molecules that repel each other will not exhibit any overlap and will show a constant effective cross-section. Alternatively, if the adsorbates migrate and form islands upon adsorption, the effective cross­section will remain constant (and smaller) throughout the dosing since each additional molecule will occupy an island edge position. As a result, the degree of interadsorbate attraction or repulsion can be determined experimentally by observing the change in effective cross-section as a function of increasing coverage.

2.2. Basic Apparatus

The instrument used for all experiments presented in this thesis has been designed to perform both helium atom reflectivity measurements (HAR) and reflectivity-detected temperature programmed desorption studies under ultra-high vacuum conditions (Figure 2-2). To achieve these objectives, the machine is composed of two sections separated by a gate valve: a bakeable scattering chamber for preparation of, experimentation with, and long-term clean storage of the target crystal and a turbopumped beamline where a high­intensity, collimated helium beam is generated by extracting the core of a high­pressure helium expansion through two stages of differential pumping.

Figure 2-2. Overview of the experimental apparatus used in these studies. Pumping (not shown) is provided by a VHS-6 diffusion pump (3000 l/s) in source chamber, a TMP-360H turbopump (400 l/s) in the 1st differential chamber, a TPU-170 turbopump in the 2nd differential chamber, and two TMP­340M turbopumps (450 l/s, each) in the scattering chamber.

The probe beam is generated by the supersonic expansion of 2 MPa of zero grade helium (Airco, 99.997% minimum purity) from a 20 m diameter nozzle held at room temperature. To maximize the beam flux, the position of the nozzle assembly can be adjusted under vacuum by means of a stepper motorized x-y-z translation stage. A 0.5 mm diameter skimmer located 15 mm away from the nozzle injects the core of the expansion into the first of two differentially pumped chambers. Two collimator plates with 3.2 mm diameter apertures located at the end of each differential chamber at respectively 10.0 and 22.5 cm from the nozzle further reduce the lateral size of the beam. At the crystal, located 54.7 cm from the nozzle, the beam is approximately four mm in diameter and has an intensity of about 10¹⁴ atoms/cm²sec.

Pumping along the beam line is provided by an unbaffled 4000 l/sec VHS-250 diffusion pump, a 360 l/sec TMP-360 turbopump, and a 170 l/sec TPU-170 turbopump in the source, first differential, and second differential chambers respectively. Typical helium loads during experiments generate pressures of up to 1 10^-4 Torr in the source chamber, 1 10^-6 Torr in the first differential chamber, and 1 10^-7 Torr in the second differential chamber. In  the crystal manipulation chamber, a pair of 450 l/sec TMP-340M magnetic bearing turbopumps maintain UHV ( 1 10^-10 Torr) when all gas sources are off and a pressure of 2  10^-8 Torr when the helium beam is admitted to the scattering chamber.

Modulation of the beam is provided by a four-vane chopper wheel located 8 cm from the nozzle. Typically, the beam is chopped at 340 Hz with a 50% duty cycle. The chopping frequency is measured by an infrared LED-photodetector assembly and used as a reference signal for a lock­in amplifier. In addition, a solenoid operated flag located in the first differential chamber is available to interrupt the beam for long periods of time.

Fixed at a right angle to the beamline, the ionizer of an Extrel quadrupole mass spectrometer used for beam detection is located 6 cm from the center of the scattering chamber. Various sized collimators mounted on the front end of the mass spectrometer with apertures ranging from 0.125 to 0.625 cm were used to selectively admit the core of the molecular beam into the ionizing region. To generate cations within the reflected molecular beam for mass selection, a hot tungsten filament was used to emit 10-15 mA of 60-80 eV electrons. For typical experimental conditions, the efficiency of the mass spectrometer for detection of nitrogen gas is rated at 10^-4.

The target crystal was polished, etched, and annealed until the exposed face was optically smooth and oriented within 0.3º of the (111) plane as determined by X-ray diffraction. For proper alignment with both the beam source and the mass spectrometer detector, the crystal is secured on a six degree-of-freedom adjustable mount (x, y, z, , , ) located in the center of the scattering chamber. A 40 watt cartridge heater mounted behind the sample and a liquid nitrogen reservoir connected to the sample mount by a copper braid provide temperature control from 125 to 1000 K. The sample temperature was monitored using a chromel-alumel thermocouple clamped between the crystal and the sample mount.

To ensure cleanliness before each experiment, the sample was heated to 850 K and bombarded with 3 keV argon ions for a period of at least 15 minutes. Following a ten minute annealing period with the temperature maintained at 850 K, the helium beam specular intensity was measured. If the resulting specular intensity corresponded to the reflectivity generally observed for a clean surface, the sample was judged to be clean. For Au(111) crystals, additional cleaning has not been observed to produce higher specular intensities than those obtained with this 25 minute cycle. However, for Ni(111) and Pt(111) surfaces, the period of exposure to argon bombardment required to fully clean the surface was typically one hour. In addition, exposure of these surfaces to oxygen gas during annealing at high temperatures (600­850 K) was observed to slightly improve the specular reflectivity.

A few of the molecules studied here, i.e. those with an activation energy for desorption smaller than 50 kJ/mol, required lower surface temperatures which could not be easily achieved in this apparatus. Reflectivity-detected TPD measurements for these molecules were carried out in the helium beam surface diffraction facility available in our laboratory. This diffraction apparatus, which has been described in detail elsewhere^,, works in a very similar way as the one described here and can achieve surface temperatures as low as 40 K but is not suitable for helium atom reflectivity measurements at surface temperatures above room temperature.

2.3. Alkane, Alkanethiol / Au(111) Experiments

2.3.1. Experimental Procedures

Dose molecule samples were purchased from Aldrich Chemical Corporation. For the n­alkanes and 1-alkanethiols, sample purity was typically in excess of 99%. For the 1­alkenes, the purity ranged from 94 to 99% with most impurities due to the presence of alkanes of similar chain length. For the more complex molecules studied in this thesis (e.g. 1,6­hexanedithiol), purity ranged from 92 to 99% with most impurities due to the presence of isomers. Liquid samples were stored at room temperature in a stainless steel tube for periods not in excess of two weeks. Gas samples were stored in their original containers and attached directly to the machine. Removal of atmospheric gases introduced during the loading procedure for liquid samples was achieved by repeated freeze-pump-thaw cycles until no impurity gases evolved from the sample container during the pump cycle.

To perform a helium atom reflectivity experiment, the gold crystal is oriented with its surface normal at 45 degrees with respect to the primary beam to direct the specular reflection into the mass spectrometer. After stabilization of the helium beam and the crystal surface temperature, data acquisition begins by establishing a clean gold specular signal intensity (Io). Dosing is achieved by the release of hydrocarbon vapor through a leak valve at the base of the scattering chamber. A diffuser plate mounted inside the chamber prevents the molecules from traveling along a direct line of sight path to the crystal. As the molecules stick to the surface, they diffusely scatter some of the incident helium beam and the specular signal decreases. If the adsorption and desorption rates are balanced, a steady-state population is formed and the specular intensity stabilizes. When the dosing is interrupted, desorption of adsorbates can be observed as a recovery of specular signal. During an experiment, dose fluxes were maintained low enough to prevent detectable attenuation of the helium beam by ambient gas in the scattering chamber.

From simple dose-desorption experiments (Figure 2-3), both the initial drop and subsequent recovery of specular signal provide useful information. At the onset of dosing, the adsorption rate can be determined by conversion of the measured decay of specular signal to an increase in absolute coverage. With the impingement rate calculated from the measurement of the partial pressure of the hydrocarbon vapor in the scattering chamber, a sticking coefficient can also be generated. After dosing is stopped, the measurement of the half-life of the specular recovery provides the desorption rate.

Figure 2-3. A sample dose-desorption run showing the decrease and subsequent recovery of the specular intensity (--, left axis) from a Au(111) crystal held at 220 K. The chamber pressure (­ - -, right axis) resulting from introduction of n-heptane to the scattering chamber is also shown.

When a set of desorption rates for different surface temperatures is obtained, an Arrhenius plot of ln(rate) as a function of inverse temperature can be formed (Figure 2-4). The slope of the best-fit line through these points is related to the energy barrier for desorption with the y­intercept equal to the natural logarithm of the pre-exponential factor. Although the slopes of the lines for the different alkane species appear to be almost parallel, all four lines converge at a y-intercept of ln(rate)  30 which corresponds to a pre-exponential "attempt frequency" of 10¹³ Hz.

Figure 2-4. Sample Arrhenius plots of experimentally determined desorption rates for four alkanes: heptane (), octane (), decane (), and dodecane (). Slopes correspond to the energy of desorption while the y-intercept provides the pre-exponential factor (typically ~ 10¹³).

To confirm the magnitude of the activation barriers to desorption as determined by the Arrhenius desorption rate plot, a second set of experiments was carried out using temperature programmed desorption (TPD). Following the deposition of adsorbates at surface temperatures which were low enough to maintain an adequate adsorbate coverage, the desorption was monitored using either the traditional method of measuring the partial pressure of desorbing species, or the more sensitive helium atom reflectivity. The temperature of the crystal was ramped at a rate of 1 to 5 K/sec during desorption. Since the helium beam is only sensitive to adsorbates on the crystal surface, errors which may arise from contributions to the traditionally detected TPD signal generated by the outgassing of the sample mount are avoided. In addition, the high sensitivity of helium scattering allows for the observation of the desorption of populations too small to be detected using traditional TPD. Although the observation of multilayer desorption or identification of desorbing species is not possible with

this technique, monitoring desorption in this way is a useful complement to traditional TPD.

Figure 2-5. Processing of specular intensity data (--) from a helium specular TPD experiment is shown for dodecane desorption from Au(111). After a correction for Debye-Waller effects(-·-·-), differentiation of resulting curve provides a traditional TPD "peak" (- - - -). If the correction is not applied (·····), the peak location does not shift significantly.

To determine the peak desorption temperatures using this approach, the mass spectrometer is tuned to m/e = 4 during the temperature ramp. To correct for the loss of specular intensity at higher surface temperatures due to inelastic scattering (Debye-Waller attenuation), the recorded helium reflectivity curve is normalized against a curve of the reflectivity of bare gold measured over the same temperature region. When the resulting curve is differentiated, a set of "desorption peaks" is generated which correspond to temperatures of greatest desorption rate (Figure 2-5). Although the amplitude of the peaks generated by this procedure may differ from those observed using traditional TPD, the temperature positions are identical within experimental error. For both TPD techniques, peak desorption temperatures (T) are converted to adsorption energies (E_ads) via the Redhead equation (Equation 2-1) and experimental values of the temperature ramp rate () and the surface vibration frequency (). Use of this expression assumes first­order desorption and a coverage-independent activation energy for desorption .

(2-1)

2.3.2. Specular Reflectivity vs. Actual Coverage

In order to obtain information about the sticking coefficient, adsorption and desorption rates, and the adsorption energies of the adsorbate/substrate system using helium atom reflectivity, it is necessary to relate the measured specular reflectivity to the actual coverage of adsorbates.

The appropriate coverage function can be readily determined for systems for which the sticking coefficient and monolayer density have been measured by Auger electron spectroscopy (AES), LEED, or other techniques. However, for the majority of the systems explored in this thesis, this information was not available. Although the sticking coefficients of the chemisorption of methane on Ni(111) and Pt(111) surfaces are well documented, reports of the sticking coefficients of alkane physisorption are limited to studies of methane, ethane, and propane on Pt(111). As a result, an alternate technique of analysis was required to relate the coverage of the long-chain alkanes and alkanethiols to observed helium atom specular intensity.

At low coverage, the adsorption process can be modeled by simple Langmuir adsorption. In this model, the number of blocked sites is directly proportional to the number of molecules adsorbed. As the coverage increases, fewer sites are available for adsorption and the overall adsorption rate will be reduced (Figure 2-6). At constant flux, this will be seen as a decrease in the rate of decay of specular intensity as a function of exposure. If the flux is known, the observed rate decrease can then be related to the surface coverage.

Figure 2-6. Specular response to increasing coverage as determined by Langmuir adsorption with constant flux and no desorption for various ordering modes: () island, (­ ­ ­) random, (····) lattice gas. Site-blocking reduces the probability of adsorption and decreases the rate of specular decay.

When estimated coverages generated by this model are compared to specular intensities, the appropriate ordering model and a value for the product of scattering cross­section () and saturation coverage (n_s) can be identified. The absolute values of , n_s, or the initial sticking coefficient (s_o) cannot be separately determined without performing several experiments at different fluxes and surface temperatures. Although the ordering model can be identified and a relative sticking coefficient and the product n_s can be found, individual parameter values cannot be assigned without additional information or assumptions.

With a rough estimate of the monolayer density, fluxes can be restated in terms of monolayers per second. Unfortunately, this data was also not available for all systems explored in this thesis. However, densities for propane through octane on Pt(111) as determined by LEED served as rough estimates. A linear extrapolation provided estimates of the monolayer density, n_s, for the longer chain hydrocarbons. The reciprocals of these densities were also used as an estimate for the hard-sphere cross-sections, which were in close agreement with cross-sectional areas reported for hydrocarbons adsorbed on graphite.

Steady-State Coverage

Two approaches were used to relate the measured specular helium intensity to the adsorbate coverage on the crystal surface for systems where the sticking coefficient was not known. The first approach relied on the generation of small steady-state coverages under particular dosing conditions. Adsorbate flux and surface temperature were selected so that the specular signal loss was typically 10 to 50%. With knowledge of an adsorption rate constant (k_a) and a desorption rate constant (k_d), the steady-state coverage () can be calculated based on the assumption of Langmuir adsorption:

(2-2)

At steady-state, d/dt = 0, so that

(2-3)

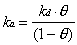
The rate of adsorption, which is equal to the product of the hydrocarbon impingement rate and the sticking coefficient, will be proportional to the partial pressure of the adsorbate vapor present in the scattering chamber. To remove the need to know either the sticking coefficient or the ion gauge sensitivity, a second experiment with the same adsorbate species can be performed at a higher flux than the first. If the surface temperature is unchanged (to maintain k_d across both experiments) and the coverage is not greatly increased (to approximately maintain the sticking coefficient), a ratio is generated which is dependent only on the measured partial pressures of adsorbate vapor of the two experiments, p₁ and p₂.

(2-4)

To use Equation 2-4 with experimental data, the measured partial pressures of the adsorbate vapor in the scattering chamber are substituted for p₁ and p₂. In the place of , one of the three surface ordering relations from Table 2-1 is expressed as a function of the observed intensity and the unknown quantity, n_s. Proper calibration is achieved when a coverage functional form and a value for n_s are found that consistently predict the specular intensity for a series of impingement rates at the same temperature.

Time-Dependent Coverage

The second approach for relating specular intensity to coverage was useful at low surface temperatures or high adsorbate fluxes, where the steady-state coverage was high. In this case, the time-dependent change in reflectivity must be monitored and related to the changing adsorbate coverage. Evaluation of the Langmuir differential equation (Equation 2-2) with a clean crystal boundary condition which assumes that = 0 at t = 0, generates the following time-dependent expression:

(2-5)

This expression may be used to compute the coverage expected at any time during an experiment where the adsorption and desorption rates are known or can be estimated.

The desorption rate constant was determined using the Arrhenius equation and a desorption energy determined by temperature programmed desorption (TPD). Alternatively, at higher surface temperatures where desorption is significant, the desorption rate constant could be obtained from the half-life of the specular intensity recovery when adsorbate dosing was stopped. To obtain the value of k_a, the Langmuir differential equation (Equation 2-2) was evaluated at the limit of zero coverage where the rate of change of coverage is independent of the rate of desorption.

(2-6)

Although (d/dt)_t=0 is not directly observable, the change in specular intensity at the onset of dosing, (dI/dt)_t=0, can be measured experimentally. These two quantities can be related by the chain rule,

(2-7)

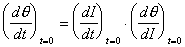
An expression for (d/dI)_t=0 can be analytically derived from the specular to coverage relationships of Table 2-1. At the limit of zero coverage, the degree of overlap is independent of the ordering mode.

(2-8)

The resulting expression for the adsorption rate constant is composed of the product of observables and one unknown quantity, n_{s. Using these values for ka} and k_d, an expression for the time-dependent coverage in terms of the measured specular intensity can be obtained. This expression can then be fit to the specular intensity data with the appropriate ordering model, cross­section (), and saturation coverage (ns) extracted from the fit.

In Figure 2-7, a sample data set has been compared to this expression for three possible ordering models and selected values of ·ns. For this particular experiment, the range of interest is from 30 to 150 seconds, where pressure and consequently the adsorption rate was held constant. The rate of desorption was estimated from measurements of the desorption half-life performed after the initial dose. If we approximate the hard-sphere cross-section of the molecule as the reciprocal of the packing density, then ·n_s will be equal to one if the effective and hard-sphere cross-sections are equal. In the experiment shown in Figure 2­7, all ordering models with a cross­section approximately eight times larger than the hard-sphere estimate provide reasonable fits to the data. However, both the exponential and polynomial curves first underestimate and then overestimate the observed specular intensity. The linear model fits the specular intensity data better across a broader region of time.

Figure 2-7. Simulated specular response during the adsorption of heptane using time-resolved model with n_s optimized: observed specular intensity (), fully random adsorption (­ ­ ­) , random on lattice sites (), islanding or repulsion (). The outlying lines (­··-··) correspond to an islanding adsorption model with the value of n_s inaccurately chosen.

Based on the analysis of many data sets of this type, the specular to coverage relationship used for physisorption of alkanes on Au(111) at low coverage favors the linear, or islanding, model of monolayer growth with an adsorbate scattering cross-section approximately eight times larger than the hard-sphere estimate. For comparison, the effective scattering cross-section of CO on Pt(111) is at least six times the hard-sphere cross-section.

2.3.3. Sticking Coefficients

Once the expression connecting the specular intensity to coverage has been determined, sticking coefficients can be derived. Since the initial sticking coefficient is defined as the rate of adsorption observed at the onset of dosing on a clean crystal divided by the impingement rate, sticking coefficients can be calculated entirely from observable quantities.

The impingement rate used in all calculations was estimated from an ion gauge measurement of the partial pressure of dose gas in the scattering chamber. To determine the actual partial pressure, a correction factor (S/S_N2) was applied to the ion gauge reading to compensate for the molecule-specific ease of ionization as well as degree of fragmentation. For the shorter chain hydrocarbons (n 7) and some cyclic molecules, these factors were available in the literature. However, for the longer chain hydrocarbons, the sensitivity factors had to be extrapolated from available data. Linear relationships of ion gauge sensitivity (S/S_N2) as a function of the number of carbon atoms in the chain, n, were determined by a least-squares fit to available data for the long­chain alkanes and alkenes:

S/S_N2 = 1.1 n + 0.4 (Alkane) (2-9)

S/S_N2 = 1.1 n (Alkene) (2-10)

For measured hydrocarbon partial pressures of 10^-9 to 10^-7 Torr, the typical fluxes are estimated to range from 10¹¹ to 10¹³ moleccm^-2sec-1.

To determine the initial rate of adsorption, the initial slope of the curve of coverage versus time is used. This often provides a satisfactory estimate; however, the initial slope may also reflect the contribution of processes other than the basic molecule-ideal surface interaction. Preferential adsorption at steps or the influence of very small populations of contaminants may alter the observed coverage increase upon dosing. Also, the dosing flux must equilibrate rapidly before the slope is altered by the presence of molecules adsorbed on the surface. Since helium atom reflectivity is sensitive to extremely small populations of molecules, the initial adsorption slope arising from slow, low-flux dosing can be determined before significant site­blocking occurs. Only large molecules which stick to chamber walls and do not reach an equilibrium pressure within seconds (e.g. C₁₆H₃₃SH) have been difficult to evaluate.

Although suitable for analysis at low surface temperatures, this simple approach begins to fail at surface temperatures close to the peak desorption temperature. This failure arises from the rapid decrease of the slope of the coverage versus time curve as the coverage approaches the steady-state population. As the surface temperature and the rate of desorption are increased, the steady-state population is reduced. As a result, the decay of the slope may begin within the region used to determine the initial slope. If a relatively large time interval is used to determine the slope, the resulting initial rate of adsorption will be an average of the true initial rate and subsequent, lower rates.

To compensate for both desorption and site-exclusion factors which can reduce the apparent rate of adsorption, the time-dependent Langmuir adsorption expression (Equation 2­2) was used. Since coverage () is known from processing of specular data, and the desorption rate (k_d) can be estimated based on surface temperature measurements, k_a can now be obtained by least-squares fit. As before, the experimental data from the first few seconds of dosing is preferably used to generate a rate of adsorption. However, using the time­dependent expression, the initial rate of adsorption can also be obtained from data outside the first few seconds of the experiment. Although other cooperative effects such as adsorbate-assisted adsorption may cause deviations from the true initial value, the flexibility provided by this technique is useful to analyze experiments that may have pressure spikes or other flaws at the onset of dosing.

2.4 Methane / Pt(111), Ni(111) Experiments

To perform the methane chemisorption experiments, two additional pieces of equipment are needed: a) the hardware to produce the excited molecules and b) a system to detect that the excitation is present. For the generation of vibrationally excited methane, a color-center laser system (shown schematically in Figures 2-8 and 2-9) was used to generate photons at 6004.844 cm^-1 which corresponds to the Q1 transition of the 2₃ asymmetric stretching vibrational mode.

Figure 2-8. Schematic of laser system showing arrangement of optical components.

Figure 2-9. Schematic of laser system showing arrangement of electronic feedback.

This light was delivered by a fiber-optic cable into a power build-up resonant cavity which was positioned in the first scattering chamber on the molecular beam path. By using a mixture of methane in helium (typically 0.5­10%) for the molecular beam, methane molecules could be initially cooled into their lowest rotational states by supersonic expansion. Exposure of the methane in the beam to a high density of photons during passage through the cavity would then vibrationally excite the methane before striking the target crystal. To detect the population of excited methane molecules in the molecular beam, a bolometer was installed in the scattering chamber. Mounted on a rotatable flange, the bolometer could be positioned to detect the energy of the molecules either before or after collision with the surface.

2.4.1. Laser System

Laser light for the experiments requiring vibrational excitation of molecules in the molecular beam was generated by a modified Burleigh 220 color center laser. Using a liquid nitrogen cooled OH^-:NaCl crystal as the gain medium, this laser is capable of providing up to 400 mW continuous power of photons in single-mode operation across the near-infrared region of 5600 to 7000 cm^-1 as shown in Figure 2-10. Continuous mode operation was required for the preparation of high fluxes of vibrationally excited methane for the adsorption experiments.

Figure 2-10. Available laser power as a function of frequency from current color-center laser system²¹.

The pumping of this color-center laser is achieved with a Quantronix 416 Nd⁺³: YAG laser and an Omnichrome 532 argon ion laser. Four watts of continuous-wave 9398.5 cm^-1 infrared light from the YAG is used to excite the color centers in the NaCl crystal. In addition, 20 mW of 19455 cm^-1 blue-green light from the Omnichrome laser is required to continually reorient the transition dipoles of the color centers (to maintain laser action).

Several sub-systems for frequency stabilization and ease of tuning have been designed into the laser system. Coarse single-mode tuning of the laser frequency is achieved by computer control of the angle of a grating (stepper-motor adjustable) and the position of an end mirror (piezoelectric). Fine frequency adjustment is achieved with analog feedback loops to optimize the etalon mirror spacing (piezoelectric) and the performance of the electrooptic crystal (piezoelectric). The resulting line width of the laser is extremely small, ~500 kHz, with little long-term drift of frequency as confirmed by minimal loss of excitation over periods of up to three hours (Figure 2­11).

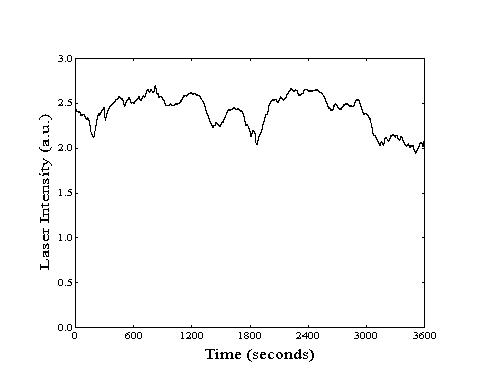
Figure 2-11. Laser stability as measured by bolometric detection of excited methane.

A Burleigh 150 MHz scanning etalon and an 8 GHz fixed external etalon were used to provide two measures of the relative frequency of the beam. These devices were also used by the analog feedback system to optimize the cavity dimensions to stabilize the frequency of the laser. For absolute frequency determination, a wavemeter was available. By mixing the light from a temperature stabilized Coherent 200 Helium-Neon laser with the output of the color­center laser, an interference pattern is generated. By counting the number of fringes with a position-scanning photodiode, the frequency could be measured reliably to within a hundredth of a wavenumber. While useful as a guide for manual adjustment of the frequency by the operator, this system was too slow to be effective for feedback stabilization of the laser.

Although output power from the color center laser was near 300 mW in the frequency region utilized (~6000 cm^-1), this intensity is attenuated significantly before reaching the build-up cavity. At typical operating intensities, 20% of the available photons are lost while passing through an Isowave Faraday isolator. An additional 10% are diverted to etalons and other devices used for feedback control and frequency determination. However, the greatest loss is due to inexact mode matching during coupling of the light into the fiber. Typically, only 50% of the light is successfully coupled into the fiber. Although a negligible number of photons are lost during the transit in the 20 meter long fiber, a maximum of only 100 mW was measured exiting the fiber. However, this loss of power was more than compensated for by the power gain obtained in the buildup cavity (see Section 2.4.2.).

The fiber used to transmit the light from the laser table to the surface analysis apparatus was terminated with an Augat Fiberoptics FC standard connector. Use of this connector allowed for easy removal and reinstallation of the fiber while protecting the exposed end of the fiber from dirt or damage. Using a junction module, a second fiber was aligned with the original fiber to deliver the laser light into the apparatus with no more than 4% loss of intensity. This fiber was epoxied in place with TorrSeal into a stainless steel tube to provide a feedthrough into the first differential chamber.

2.4.2. External Resonant Cavity

To generate a high concentration of photons within a confined region for the vibrational excitation of the molecular beam, a commercially available Fabry-Perot interferometer was used as a "power build-up cavity". Intended for use as a multimodal spectrum analyzer, the SR-170-C Supercavity from Newport has been frequently used by members of the Scoles group as an alternative to multipass cells. While a well-aligned multipass cell can make a photon cross a molecular beam 60 times, supercavities are able to achieve photon residence times equivalent to 500­1000 crossings. In addition, since the light in a supercavity travels along the central axis of the cavity, there is no Doppler broadening (intrinsic to most traditional multipass cells).

The SR-170-C Supercavity consists of two spherical mirrors separated by a piezoelectric tube. The distance between the mirrors can be adjusted by applying the appropriate voltage (0­400V) to the piezoelectric. As the length of the cavity changes, the resonant frequency of the cavity will also be altered. If the frequency of the incident light and the resonant frequency match, the photons will enter the cavity and accumulate.

The peak intracavity power will be primarily related to the incident power (I_o) and the performance specifications of the mirrors: reflectance (R), transmittance (T), and absorbance (A). To determine how much light is stored in the cavity, the amount of light that "leaks" out can be measured with a photodiode. At the resonant condition, the intensity of light transmitted through the cavity (I_t ) is given as:

(2-11)

Since Equation 2-11 only considers the light exiting the cavity through the back mirror, a factor of two must be added to account for transmission through both mirrors. This is offset by the fact that the light inside the cavity (with intensity I_ic) will have an equal probability of traveling towards either mirror. As a result, the transmitted intensity of light will be given as I_t = I_ic · T. Substitution of this expression into Equation 2-11 allows the intracavity intensity to be calculated:

(2-12)

The reflectance of the supercavity mirrors (R) can be calculated from a performance measure known as the finesse of the cavity. Finesse (F), which is also related to the frequency resolution of the cavity, is equal to

(2-13)

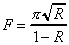
For a typical Newport high-transmission supercavity, the finesse is reported as 5000. Using this value and Equation 2-13, a reflectance of 0.9994 is calculated. If half of the remaining light is absorbed by the mirror (a high estimate), the probability of transmittance is 0.0003. Using these values and Equation 2-12, the equivalent number of crossings, given by the ratio of I_ic / I_o, can be calculated as 800 in this example.

2.4.3. Apparatus for Cavity Alignment

In order to ensure high-efficiency operation, the alignment of the supercavity was designed to be adjustable with respect to the optical fiber and the molecular beam. Improper alignment of the supercavity with the optics would reduce the amount of intracavity power available. Similarly, misalignment of the supercavity with the molecular beam would potentially result in blocking or missing the molecular beam. A compact supercavity mount system (Figure 2­12) was developed to meet both functional requirements while still fitting within a 10 cm diameter size constraint.

Figure 2-12. Supercavity mounting assembly. Entire apparatus is designed to mount on a six inch conflat flange which is installed on the first differential chamber of the experimental apparatus.

The optical fiber is mounted on a Newport FP-2 fiber positioner for adjustment across five degrees of freedom (x,y,z,,). All grease and plastic components of the mount were removed prior to installation to ensure high-vacuum compatibility. Light from the optical fiber is directed towards a gradient index (GRIN) lens which is positioned 2.08 mm away from the end of the fiber. Fixed on a non-adjustable aluminum pedestal, the GRIN lens provides for the focusing and mode-matching of the light from the fiber into the supercavity. The supercavity, located 18 mm away from center of the GRIN lens, is also mounted on an FP-2 adjustable mount which has been modified to accommodate the wider diameter of the cavity. By holding the GRIN lens in a fixed position, only two adjustable mounts are required, thus reducing space requirements and cost.

To adjust the position of the supercavity with respect to the molecular beam, two translation stages are used to provide motion along the two axes oriented normal to the path of the molecular beam. An adjustment for the distance between the skimmer and the supercavity (along the path of the molecular beam) was determined to be unnecessary. For motion along the horizontal axis, the three optical components were bolted onto a brass plate which was designed to slide within an aluminum track. An 80 t.p.i. shaft driven by a stepper motor moves the plate at a rate of 80 nm/step across a maximum of 1.0 cm of travel. This aluminum track assembly also makes up the base of an L-shaped piece which is attached to a six inch conflat flange by a commercially available translational stage. This stage is driven by a stepper motor which has been substantially geared down for precision motion along the vertical axis. By moving the optical components of the assembly as a unit, optimization of the alignment of the molecular beam with the supercavity will not affect the relative alignment of the optics. As a result, all optimization of the alignment of the optical components could be performed manually outside the vacuum system prior to installation.

To avoid loss of excitation due to Doppler splitting, all elements were precisely assembled to ensure that the supercavity was oriented normal to the path of the beam. However, during alignment of the cavity with the fiber, minor angular deviations of the cavity off-normal resulted occasionally. Although large deviations required realignment, small corrections could be performed by precise adjustment of the conflat flange onto the first differential chamber. By overtightening bolts on one side of the flange, the alignment of the build-up cavity could sometimes be restored to the normal orientation.

Performance of the cavity was measured by a germanium photodetector which had been mounted on the rear mirror of the supercavity located opposite the fiber. When the resonant frequency of the supercavity matched the frequency of the incoming light, photons traveled through the cavity to the photodetector. Alignment of the optics was evaluated by providing single-frequency light to the cavity while ramping the voltage supplied to the piezoelectric tube. When the cavity is misaligned, the cavity will support several higher-order modes and the resulting intensity of transmitted light for any individual mode will be weak. With proper alignment, only one mode will be supported with high transmitted intensity. Continual testing of alignment after several months of operation under vacuum has shown very little drift with no more than two modes supported.

2.4.4. Detection of Vibrational Excitation: Principle of Operation of the Bolometer

A bolometer was installed on the scattering chamber to be used primarily for the detection of vibrationally excited molecules in the incident beam. By quantifying the amount of energy deposited by impinging gas atoms, the bolometer could determine both the total beam flux and the percentage of molecules which were excited by passage through the build-up cavity. In addition, the bolometer was also used as a complement to the mass spectrometer for the measurement of the intensity of the specular reflection without the potential for adsorption induced by the presence of the ionizer filament.

The core of the bolometer detector consists of a small crystal of germanium suspended by two gold lead-wires. As the crystal temperature is reduced to cryogenic temperatures, the carrier mobility of the crystal decreases which results in an exponential increase in the resistance. For the bolometer installed on this apparatus, the resistance increases from 12  at room temperature to 10 M at the operating temperature, 1.6 K.

When a molecular beam impinges on the bolometer surface, energy will be transferred from the gas to the crystal. This energy momentarily heats the bolometer and reduces the resistance. With a battery providing constant current through the bolometer, a voltage drop across the bolometer can be measured. This drop will be directly proportional to the resistance which can then be related to the quantity of energy deposited. With a peak sensitivity to energy transfer of 10^­13 watt, experiments are typically performed with a chopped beam to isolate the signal due to the beam from the background radiation.

The majority of the detected energy is translational energy transferred from the gas to the surface during the collision. If the gas becomes adsorbed on the surface of the bolometer, additional energy may be deposited. The energy of condensation as well as the vibrational and rotational energy of the gas will be transferred to the bolometer, increasing the observed change in resistance. In this way, the presence of vibrationally excited molecules in the molecular beam can be selectively detected by modulation of the laser intensity entering the build-up cavity. For a fully accommodated methane molecule excited in the 2₃ mode, 71 kJ/mol of vibrational energy and 24 kJ/mol of translational energy will be transferred to the bolometer. When the molecular beam is constant and the laser beam is chopped, only the first of these two energies will contribute to the signal detected by the bolometer.

2.4.4.1. Bolometer Design

The temperature sensor of the bolometer is a small germanium crystal. However, to increase the size of the detector without increasing thermal response time, a sapphire crystal (3.0 × 0.3 mm) has been attached. At low temperatures, the heat capacity of sapphire is significantly less than that for germanium. In addition, the thermal conductivity of sapphire is also greater than that of germanium. Two gold wires connect the bolometer to the detection circuit while also providing (poor) thermal contact with the liquid helium dewar.

The bolometer is housed in a gold-plated copper mount with two entrance holes for exposure to the molecular beam (Figure 2-13). On the side facing away from the sample mount at the center of the scattering chamber, a 0.5 mm diameter aperture has been placed for detection of the incident molecular beam. On the side facing the crystal, a slit entrance (3.0 × 0.3 mm) is aligned directly over the bolometer to provide for detection of the scattered beam. Both openings are located 5.0 mm away from the bolometer so angular resolution is high and proper alignment is crucial.

Figure 2-13. Bolometer housing design. Bolometer can be exposed to the molecular beam through the front slit or through the larger aperture located on the back side of the mount.

To cool the bolometer, the bolometer mount is attached to a liquid helium dewar by four screws. Pure indium metal has also been placed between the base of the bolometer mount and the dewar to increase thermal contact. To reduce the temperature of the liquid helium to below 2 K, the vapor pressure above the liquid is reduced by a 12 l/sec E2M40 Edwards rotary pump with roots blower. At this temperature, liquid helium is also a superfluid with extremely high thermal conductivity, eliminating the noise induced by bubble formation due to boiling.

Additional protection of the liquid helium cooled components from ambient radiation is provided by a liquid nitrogen cooled shield made of OFHC copper. The majority of the shield consists of a copper tube, approximately 1.0 cm larger in diameter than the liquid helium dewar. A copper end-cap which shields the bolometer mount has two slits 1.5 mm wide to allow for alignment of the bolometer with the aperture. The size of these slits was adjusted with razor blades down to approximately 0.5 mm to minimize thermal radiation exposure and to provide a knife-edge precision edge.

The cryostat assembly was mounted on a bellows to allow for height adjustment of the bolometer (Figure 2-14). A gate valve located between the bellows and the scattering chamber could be closed to fully isolate the cryostat and to protect it from the high-temperature baking of the UHV scattering chamber. This isolation also allowed the cryostat to cool and condense contaminants before reinsertion into the scattering chamber at the beginning of an experiment. The assembly was also mounted on a rotatable flange to provide full 360º rotation of the bolometer.

Figure 2-14. Side view of bolometer and cryostat assembly.

Signal detection made use of a circuit designed to amplify the signal while protecting the bolometer from damage due to accidental high-temperature, low-resistance operation (Figure 2­15). The load resistor (10 M) was mounted in series with the bolometer to minimize the current flow and power dissipation. Outside the cryostat, the small bolometer signal was amplified 200­1000 times with a low-noise, op-amp based circuit. This amplified signal was processed by a lock-in amplifier to detect the magnitude of the modulated signal.

Figure 2-15. Bolometer circuit for Infrared Laboratories LN-6C preamplifier.

2.4.4.2. Accommodation

Unlike more massive atoms or molecules, helium will not readily condense on the bolometer upon collision. The disparity between the mass of the helium atom and the effective mass of the surface predicts that such a collision is highly elastic. In addition, the small binding energy of physisorption of helium reduces the likelihood that the atom will become bound on the surface for sufficient time to fully accommodate. As a result, only a fraction of the translational energy of the incident helium atoms will eventually be transferred to the surface.

To estimate the maximum quantity of translational energy that can be deposited onto the bolometer during a gas-surface collision, the hard-sphere collision model can be used. In this model, only translational energy along an axis normal to the surface is considered. For an incident particle with mass m_i colliding with a surface with effective mass m_s, the amount of translational energy (E_i) transferred to the surface is given by E_s in Equation 2-14.

(2-14)

While the mass of the incident particle is known, the effective mass of the surface must be determined by simulation or experiment. An analysis of velocity distributions of argon scattered from tungsten indicated that the effective mass of the surface could be related to the speed of the sound in the substrate and the collision time. In effect, the effective mass could be determined by the number of surface atoms involved in the collision event. For xenon atoms with translational energies greater than 1 eV incident on Pt(111) at room temperature, the effective mass was found to be approximately equal to 3 atoms. Since the speed of sound is 12 times slower at 2 K than at 300 K, the effective mass of the bolometer will be expected to be significantly lower.

To determine the relative accommodation coefficients for helium and a variety of gases experimentally, the bolometer was positioned to intercept the center of the incident molecular beam. By comparing the response of the bolometer to the translational energy of the incident molecular beam, an accommodation factor could be calculated. The signal resulting from the transfer of energy from the incident molecules to the bolometer ("Bolometer Signal" in Table 2-2) was recorded for molecular beams of five gas mixtures generated at backing pressures of 50 and 150 p.s.i. All experiments were performed with a nozzle temperature of 475 K to minimize cluster formation in the supersonic expansion.

At the bolometer, located 42 cm from the nozzle, the beam intensity was uniform across the width of the molecular beam. As a result, the flux on the bolometer was proportional to the total flux ("Total Beam Flux") entering the scattering chamber. This flux was estimated from the partial pressure rise induced by the admittance of the molecular beam into the scattering chamber which was measured by a sensitivity-corrected ion gauge. Prior to the pressure measurement, the bolometer and cryostat assembly were removed from the scattering chamber to eliminate any chamber pressure reduction due to cryopumping.

The translational energy of the incident atoms in the beam was estimated for each gas as 5/2 kT, or 10 kJ/mol at a nozzle temperature of 475 K. The relative level of accommodation ("Transfer") was calculated as the response of the bolometer to the total energy of the molecular beam. This factor is equal to the observed bolometer signal (in Volts) divided by the product of the total beam flux (mol/sec) and the translational energy (kJ/mol). Since the actual voltage response of the bolometer per unit energy is independent of the gas composition, variations in the calculated "Transfer" value must result from differences in the degree of accommodation. For the heavier species, increasing mass does not increase the amount of energy transferred to the surface, indicating that complete accommodation is occurring. For helium, the amount of energy transfer is approximately 50% less. This factor of two difference in accommodation between helium and methane will be used to calculate the extent of vibrational excitation in the following section.

2.4.4.3. Bolometer Experiments

Two types of experiments were performed with the bolometer and a lock-in amplifier: detection of molecular beam modulation and laser intensity modulation. To determine the total energy of the molecular beam, the laser was blocked and a four-vane chopper located in the first differential chamber was used modulate the beam at ~200 Hz. Alternatively, to measure the energy and quantity of the vibrationally excited molecules, the beam chopper would be stopped in the open position while a chopper mounted on the laser table would modulate the light before entering the fiber at a rate of ~340 Hz. Bolometer response and sensitivity to modulation at the two frequencies was observed to be similar to within 10% for all frequencies between 120 and 400 Hz. Across this frequency region, noise was particularly bad at 240 Hz and other line-noise (60 Hz) higher-order harmonics.

Beam Profile Diagnostic

To properly align the build-up cavity with the molecular beam, the bolometer was used to measure the population of the vibrationally excited molecules as a function of location within the beam. To generate a "profile" of the total beam or the vibrationally excited molecule intensity, the vertical position of the bolometer was manually adjusted at a constant rate while the bolometer signal was recorded. The two profiles could then be compared to determine if the center of the region of laser excitation coincided with the center of the molecular beam. Any deviation could be corrected by adjustment of the build-up cavity vertical position with a stepper motor. An example of a profile showing proper alignment is shown in Figure 2-16.

Due to the finite width of the bolometer across the direction of motion, the measured beam and laser intensity profiles do not indicate the true intensity at each bolometer location. Since the measured signal at each location corresponds to an average of intensities across the width of the bolometer, the measured intensity profiles are broader and smoother than actual. Although the centers of the profile features are not shifted by this effect, the "blurring" effect due to the width of the bolometer can be deconvolved from the true data.

Figure 2-16. Bolometer signal intensity profile generated by lock-in detection of modulation of the molecular beam (---) or the laser (- - -).

If the measured intensity at each position (I_n) is assumed to be the average of the true intensity (S_i) detected across the width of the bolometer (2·w), we can approximate the measured intensity at point n as:

(2-15)

If the intensities of the measured signals at two adjacent locations are compared, the result provides information about the true intensity at two locations separated by the width of the bolometer.

(2-16)

When the bolometer is positioned at the edge of the beam, only a part of the bolometer will intercept the beam. Depending on the orientation of the bolometer with respect to the beam, the true intensity at one end of the bolometer (either S_n+w or S_n-w) will be equal to zero. As a result, Equation 2-16 can be first applied to determine the value of the true intensity at the opposite end of the bolometer which is in the region of intercept. Equation 2-16 can be rewritten to calculate the true intensity (S_n±w) at this location as a function of measured intensities:

(2-17)

With Equation 2-17, the value of the true intensity can be calculated from measured intensities for bolometer positions within a distance of 2w of the edge of the beam. These values can then be used with additional measured intensity data and Equation 2-16 to calculate the true intensities at locations deeper within the molecular beam. The results of this deconvolution is that the amplitude of the peaks will be slightly increased and the slopes are sharpened as the "blurring" effect is removed (Figure 2-17).

Figure 2-17. Sample original (- - -) and deconvolved (--) laser profile data from Figure 2-16.

Due to the recursive nature of this procedure, caution must be used to avoid amplification of errors. Any sharp discontinuities or spikes in the data will be reproduced repeatedly at locations separated by 2·w. In addition, the rate of bolometer motion must be relatively constant otherwise this process will not accurately recover the original data. Although not necessary for this analysis technique, a complete scan across the beam is recommended so that this deconvolution process can be run in both directions to confirm the presence of recovered features.

Probability of Vibrational Excitation

By quantifying the bolometer response to the total energy of the beam, the sensitivity of the bolometer can be determined. The bolometer signal (I_beam) resulting from a chopped incident molecular beam will be a function of the translational energy of the helium and methane molecules, the fraction of methane in the beam (p_CH4), the accommodation factor of each gas (), and the bolometer response factor (b). Due to the seeding effect, the average velocity of the helium atoms and the methane molecules will be equal. The velocity (v) of both species can be calculated as a function of the nozzle temperature (T) and the average mass of the gas mixture (m_avg) in Equation 2-18.

(2-18)

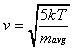
As a result, the translational energy of each species is equal to

(2-19)

Using the expressions of Equation 2-19, the intensity of the molecular beam signal is equal to

(2-20)

A similar expression can be derived for the bolometer response to modulation of the laser intensity (I_Laser). Only vibrational energy (h) deposited by the fraction of vibrationally excited methane molecules (e) in the beam will be detected by this experiment.

(2-21)

In both cases, the bolometer response factor (b) will contain information about the flux of the beam, the area of the bolometer, and the response of the bolometer to incident energy. For small energy transfer loads, this factor will remain constant across both experiments.

An initial estimate of the bolometer signal (I_Beam) to determine b can be obtained by integrating the intensity profiles across the entire width of the beam (or across only the region which will be detected for helium specularity measurements). However, since each profile only represents the intensities of a narrow strip of points measured along the diameter of the molecular beam, the data must be weighted to account for the total area of the cross-section of the molecular beam (Figure 2-18).

Figure 2-18. The profile of Figure 2-16 corresponds to the intensities of a single strip of points within the molecular beam. Since the signal intensities at all points equidistant from the center of the molecular beam are equivalent, the profile data must be weighted by 2r to account for the total beam.

Since each point in the one-dimensional profile is equivalent to a ring of points with circumference 2r around the center of the molecular beam, the correction can be applied by multiplying the signal intensity by the distance of the bolometer from the center of the beam at each point.

By integrating the weighted profile data for a modulated molecular beam experiment to determine I_Beam for use in Equation 2-20, a value for b can be calculated. This value can then be used with Equation 2­21 and the integrated weighted profile data for a modulated laser experiment to determine the fraction of excited seed molecules in the beam. Profile data from typical laser experiments performed with a room temperature nozzle show that up to 7% of the methane in the total molecular beam was excited under typical time-averaged laser power of 45 mW. Experiments performed with the laser unmodulated would effectively double the average laser power and the percentage excited; however, this could not, of course, be experimentally confirmed because of the lack of lock-in detection of the excited molecules.

Due to the small focal region in the build-up cavity, only the core of the molecular beam will be vibrationally excited. As a result, the percentage of excited methane molecules will also differ as a function of distance from the center of the beam. To determine the maximum percentage of excitation, only the core of the profiles (within 0.5 mm of the beam center) was integrated. Using Equation 2-20 and the molecular beam modulation profile, a new value of b was calculated for use in Equation 2-21 to calculate the percentage of excitation within the smaller integration region. With this technique, the average percentage of excitation at the center of the beam during a modulated laser experiment was calculated to be 22%. Due to the presence of a collimator plate in front of the ionization region of the mass spectrometer, only the reflection of a 1.3 mm diameter region of the molecular beam is monitored to perform helium atom reflectivity. Within this slightly wider integration region, the average percentage of excitation during a modulated laser experiment can be calculated as 18%.

The theoretical maximum extent of excitation is determined by the degree of rotational cooling in the supersonic expansion and the nuclear spin partition function of the molecule. For methane, three nuclear spin states are possible: A, E, and F. Using Boltzmann statistics and the degeneracy of each rotational level for each nuclear spin state, the percentage of total methane in each state can be calculated (Table 2-3).

At room temperature (298 K), the equilibrium distribution of molecules among the A, E, and F states is 31, 13, and 56%, respectively. However, during the short time scale of a supersonic expansion, molecules in these three states are unable to interconvert when subjected to rapid cooling. Therefore, not all rotational states are available to the molecules of each of the three species. As a result, the molecules of each nuclear spin species will cool as three independent populations into the lowest rotational states for each of these species (Table 2-3). Since the laser is only able to vibrationally excite molecules in one rotational state for a given frequency, the nuclear spin statistics will reduce the population available for excitation.

The final rotational temperature of the molecules in the expansion from a room temperature nozzle was determined experimentally by measuring the relative intensity of the Q1 and Q2 lines of the 2₃ asymmetric stretch. To reproduce the observed ratio of absorption intensities (I_Q1 / I_Q2 = 3.89), the rotational temperature was calculated to be 7.4 K. Calculations of the populations of each rotational and nuclear spin state are shown in the rightmost columns of Table 2-3. By vibrational excitation of the Q1 branch for the laser experiments (requiring the population to be in the J=1 state before excitation), a maximum of 54.7% of the methane in the beam produced by expansion from a room temperature nozzle may be excited by adiabatic rapid passage through the build-up cavity.

2.4.5. Methane Sticking Coefficient Measurements: Experimental Procedure

To determine the rate of adsorption of ground-state and vibrationally-excited methane on transition metal surfaces, the specular reflectivity of Pt(111) and Ni(111) crystal surfaces were monitored as a function of exposure to a molecular beam of research grade helium (Spectragas, 99.9999%) which had been seeded with methane (typical concentrations were 0.5 to 10% CH₄ in helium). In this way, the translational energy of the methane could be controlled by adjustment of the nozzle temperature with a 40 W cartridge heater. In addition, the helium atoms present in the beam could be used for helium atom reflectivity to monitor the population of adsorbates.

Prior to the experiment, the surface was cleaned with argon ion sputtering and annealing. In addition, a small amount of oxygen gas was admitted to the scattering chamber to "burn" off any adsorbates left behind by the sputtering process. After confirming the cleanliness of the crystal by measuring the specular intensity and comparing it to the intensity expected for a clean surface, the bolometer was rotated into place to intercept the molecular beam. By chopping the laser and using a lock-in amplifier to detect the modulation of the laser intensity, the laser was tuned to produce photons of the appropriate frequency to maximize the extent of vibrational excitation in the beam.

After a small equilibration period to confirm the stability of the laser, the bolometer was rotated out of the way to allow the molecular beam to strike the crystal. The specular reflection of the helium in the molecular beam was monitored with the mass spectrometer as before. The crystal was exposed to the beam for periods of up to 250 minutes depending on the stability of the laser. Following exposure, the bolometer was rotated back into the path of the beam to confirm that the laser had not drifted during the experiment.

Several variations of experiments were performed during the period of exposure of the crystal to the molecular beam. To determine the rate of adsorption with vibrationally excited methane (an experimental cycle referred to as "laser on"), laser light was admitted to the cavity while the rate of specular decay was monitored. To determine the baseline rate of adsorption with ground-state methane ("laser off") a beam stop was placed in front of the fiber to prevent transfer of light into the cavity. Alternatively, to measure the rate of adsorption of contaminants present in the scattering chamber ("helium"), pure helium would be admitted through the nozzle instead of the helium/methane mixture. A fourth type of experimental cycle which effectively doubled the time-averaged laser power ("double"), was performed by deactivating the laser chopper to remove the modulation of the laser during the adsorption experiment. Although this process increased the duty-cycle of the laser from 50 to 100%, it was observed to destabilize the laser slightly and increased the risk of laser drift during experimentation.

A typical experiment would consist of a "laser on", "laser off", and a "helium" cycle (Figure 2-19). Conversion of the specular intensity data to coverage was performed as described in Section 2.3.2. The rates of adsorption observed during the "laser on" and "laser off" cycles would first be adjusted to account for the rate of adsorption of background gases during the "helium" cycle. The two resulting methane adsorption rates would then be compared to determine if there was any change in the rate of adsorption attributable to the presence of vibrationally excited methane.

Figure 2-19. Sample methane adsorption experiment on Pt(111) with thirty minute cycles of "laser on", "laser off", and "helium". Higher specular signal during exposure to helium is due to differences in backing pressure.

2.4.5.1. Average Beam Velocity Measurement

For a molecular beam formed from a pure gas with atomic weight (m) at a nozzle temperature (T), the velocity of the molecules (v) can be estimated from the translational energy equation:

(2-22)

However, for a gas mixture, the velocity of the heavier molecules of the molecular beam will be higher than predicted by this relationship. At small concentrations of heavy molecules "seeded" in a light gas, the velocity along the beamline of both beam components will be equal. However, this seeding effect will become gradually diminished as the concentration of heavy molecules is increased. To determine if the velocity enhancement due to the seeding effect was independent of the concentration of methane used in the experiments of this thesis (0.5-10%), the velocity of the methane molecules was measured using a modified time-of flight technique.

Due to the location of the mass spectrometer with respect to the beamline, the molecular beam could only be detected after specular reflection from the surface. As a result, some increase in travel time was expected to occur due to possible energy loss of the beam on the surface. However, since the distance from the crystal to the ionizer of the mass spectrometer (6 cm) is significantly less than the distance from the beam chopper to the crystal (52 cm), the total travel time would not be significantly increased. In addition, the determination of average velocities was sufficient to determine if the seeding effect was constant across the range of methane concentrations.

The beam velocity (v) was estimated from the measured phase difference () between the chopper photodiode signal and the mass spectrometer signal for a series of experiments at different chopping frequencies (f) with Equation 2­23. The ratio of the distance from the chopper to the ionizer region of the mass spectrometer (d) and the velocity (v) provides the actual travel time.

(2-23)

In Equation 2-23, the response time of the mass spectrometer and support electronics is accounted for by a factor () which was assumed to be constant in all experiments. An additional phase factor of x90 was required since the measured phase difference could be referenced to the leading edge, the center, or the trailing edge of the square pulse of the modulated signal by the lock-in amplifier used to perform these experiments. Sample phase data are shown in Table 2-4 for a molecular beam consisting of 2% methane in helium generated at two nozzle temperatures, 300 K and 450 K. During these experiments, the mass spectrometer was tuned to m/e = 15 to detect the methane in the molecular beam.

Before using Equation 2-23 to find the velocity of the molecular beam, the value of x must be determined. With the same molecular beam composition and nozzle temperature, two experiments are performed at different chopping frequencies. Since the time of flight and response time will be the same for both experiments, Equation 2-23 can be rewritten to find x from the frequencies and observed phase differences.

(2-24)

Using this technique, x was determined to be approximately equal to one for the experiments reported in Table 2-4. As a result, 90° is added to the measured phase differences to generate the actual phase difference.

With the true phase difference known, the relative velocity of the molecular beam can now be calculated. Using Equation 2-23 and two different nozzle temperatures, two equations for the two unknowns (v₁, v₂) can be generated. For the phase difference data of Table 2-4, the average velocity of the molecular beam formed from a nozzle at 300 K is calculated to be 1610 m/s; at 450 K, 1970 m/s.

2.4.5.2. Adsorption on Pt(111)

The specular decay curve resulting from the exposure of the Pt(111) crystal to adsorbates showed evidence of adsorption at two different sites (Figure 2-20). For exposure to a constant flux of adsorbate vapor, the specular intensity decayed rapidly to 85% of its original value before decaying at a slower rate. This change in slope was reproducible regardless of cleaning, annealing, or intentional damage of the crystal with the argon ion sputter gun. The decay behavior was also independent of the choice of adsorbate or the use of oxygen to clean the surface.

Figure 2-20. For adsorption on Pt(111), the initial rate of specular decay was observed to be ten times more rapid than the long-term rate. Two concentrations of methane in helium are shown for comparison.

Based on the scattering cross-section of adsorbed methane and other small molecules, this initial specular decay corresponds to a coverage of approximately 1% of all available sites. This population estimate was confirmed by performing TPD after exposure of the clean, well-annealed Pt(111) crystal to CO. Integration of the two peaks which result from desorption from a low-energy "terrace" site and a higher-energy "step-edge" site (Figure 2-21) provides the relative population at each site. For exposures that produce a full coverage of CO adsorbates, the ratio of populations is approximately 40:1, corresponding to a step/defect density of 2.5% of all available sites.

Figure 2-21. Helium reflectivity TPD of CO from Pt(111). Two desorption peaks are observed corresponding to activation energies of 122 and 135 kJ/mol.

As a result, it is believed that the initial rapid specular decay is due to the presence of step-edges which provide binding sites with a reduced activation energy to adsorption. Selective adsorption at surface defects and other lower activation energy sites has been commonly observed for several systems (e.g. CO on Pt(111), O₂ on Ag(001), C₂H₆ on Ir(111)). These sites are rapidly filled and do not significantly affect further adsorption; however, the extreme sensitivity of helium atom reflectivity has made them observable. To avoid variations in the observed sticking coefficient resulting from adsorption at the special sites, any comparisons between rates of adsorption for "laser on" and "laser off" experiments are made only for similar adsorbate coverages. Due to the rapid depletion of step-edge sites, adsorption rate measurements in the long-term slope region were easier to perform and more precise.

References