|
|||||||||||||||
|
|
|||||||||||||||
|
|
|
|||||||||||||
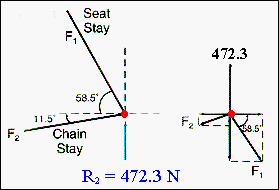
| If
the rear triangle is taken to be a jointed triangular structure, the tubes
are either in pure tension or pure compression and the joints are in static
equilibrium with no net forces or moments acting on them. This approximation
can be used to estimate the forces acting in the chain stay (F1)
and the seat stay (F2) when the reaction force at the rear axle
is 472.3 N.
If the forces acting on the joint are resolved into horizontal and vertical components then these must each have a net zero value. For
the horizontal forces: F2 cos (11.5) = F1 cos (58.5)
or: F1
= F2 {cos (11.5)/cos (58.5)} = 1.88 F2.
|
|||||||||||||||
 |
|||||||||||||||
| From:
McMahon and Graham:
"The Bicycle and the Walkman," Merion (1992) |
|||||||||||||||
| For
the vertical force balance: R2 = F1 sin(58.5) + F2
sin(11.5), so that when the above value of F1 is substituted
into the equation it is found that : F2
= 262.2 N.
Using this value to evaluate F1 gives:
F1 = 490.9 N. The sign of these forces has not been given but from inspection it is seen that the seat stay is in compression and the chain stay in tension. This proceedure may be used to evaluate the force in the seat tube and top tube of this pinned structure. Force in seat tube = 119.8 N, force in top tube = 221.7 N. |
|||||||||||||||