| |
Torsional
Loads
Components
of human-powered vechicles, such as the shaft in
the bottom bracket of a bike, the propeller shaft of an aircraft or boat, or
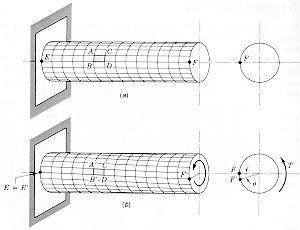
the wing of an aircraft, are subject to torsional loads. The top diagram shows
a shaft that is fixed at one end and has a torque, T, applied to the free
end. This causes the shaft to twist as shown in (b) and the outer elements of
the shaft experience a maximum shear stress, tmax = (TR/J) where R is the
shaft radius and J is the polar moment of inertia of the shaft. For the cylindrical
shaft shown,
J = pR4/2.
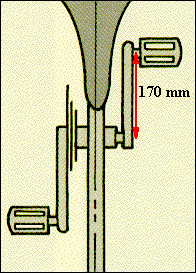
If the
pedal force is 800 N, T = 136 N.m, and for a shaft of 20 mm diameter, J = 1.6 x 10-8 m4.
If the shaft is fixed at one end by tension in the chain but free to rotate
at the other end, the maximum shear stress in the shaft is 170 MPa. If the shaft
has a length L =100 mm and has a shear modulus, G = 200 GPa, then the twist f =
(TL/JG) = 4 x 10-3 radians = 0.03 degrees, a suitable design value.
Similar calculations
can be used for a propeller shaft where the torque is that required to turn
the propeller. For a tubular shaft, J = (p/2){R4
- r4} where r is the inner radius. |
|
|
|
|
|
|
|
|
|
|
|