Streamlines and Streamtubes

A streamline is a line that is tangential to the instantaneous velocity direction (velocity is a vector, and it has a magnitude and a direction). To visualize this in a flow, we could imagine the motion of a small marked element of fluid. For example, we could mark a drop of water with fluorescent dye and illuminate it using a laser so that it fluoresces. If we took a short exposure photograph as the drop moves according to the local velocity field (where the exposure needs to be short compared to the time it takes for the velocity to change appreciably), we would see a short streak, with a length V \Delta t, and with a direction tangential to the instantaneous velocity direction. If we mark many drops of water in this way, the streamlines in the flow will become visible. Since the velocity at any point in the flow has a single value (the flow cannot go in more than one direction at the same time), streamlines cannot cross. except at points where the velocity magnitude is zero, such as at a stagnation point.

There are other ways to make the flow visible. For example, we can trace out the path followed by our fluorescent drop using a long-exposure photograph. This line is called a pathline, and it is similar to what you see when you take a long-exposure photograph of car lights on a freeway at night. It is possible for pathlines to cross, as you can imagine from the freeway analogy: as a car changes lanes, the pathline traced out by its lights might cross another pathline traced out by an adjoining vehicle at a different time.

Another way to visualize flow patterns is by streaklines. A streakline is the line traced out by all the particles that passed through a particular point at some earlier time. For instance, if we issued fluorescent dye continuously from a fixed point, the dye makes up a streakline as it passes downstream. To continue the freeway analogy, it is the line made up of the lights on all the vehicles that passed through the same toll booth. If they all follow the same path (a steady flow), a single line results, but if they follow different paths (unsteady flow), it is possible for the line to cross over itself.

In unsteady flow, streamlines, pathlines and streaklines are all different, but in steady flow, streamlines, pathlines and streaklines are identical.

Streamtubes

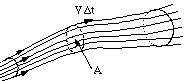
Imagine a set of streamlines starting at points that form a closed loop (figure 18).

Figure 18. Streamlines forming a streamtube.

These streamlines form a tube that is impermeable since the walls of the tube are made up of streamlines, and there can be no flow normal to a streamline (by definition). This tube is called a streamtube. From mass conservation, we see that for a steady, one-dimensional flow, the mass-flow rate is constant along a streamtube. In a constant density flow, therefore, the cross-sectional area of the streamtube gives information on the local velocity.

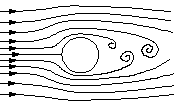
As an example, consider steady, constant density flow over a cylinder, where the cylinder axis is normal to the direction of the incoming flow (figure 19).

Figure 19. Flow over a cylinder.

Far upstream of the cylinder, the flow is uniform in all directions (we could call this a zero-dimensional flow). The flow near the cylinder varies in the streamwise and normal directions but not in the spanwise direction. So the flow near the cylinder is two-dimensional. In this region the streamlines come closer together, and the area between them decreases. Since the density is constant, the velocity must increase according to the principle of mass conservation. For constant density flow, wherever the area between streamlines decreases, the velocity increases. This is exactly similar to what happens with constant-density flow through a duct or a pipe --- if the area decreases, the velocity increases so that the volume flow rate is maintained constant (volume flow rate out must equal volume flow rate in by continuity). At a reasonable speed for a reasonably sized cylinder (more precisely, at Reynolds numbers that are not too small), the maximum flow velocity in the region where the streamtubes take their minimum area is about 1.74 times the velocity in the far-field.

As the flow passes over the shoulder of the cylinder, it separates (we saw a similar separation phenomenon in the diffuser flow shown in figure 10). Large eddying motions form in the wake of the cylinder, and the wake flow is unsteady and three-dimensional. Streamlines become very difficult to visualize and interpret in this region.

Return to Aerodynamics of Bicycles Introduction.