M2Spice: Advanced Tools for Planar Magnetics Modeling
M2Spice is a standalone open-sourced software that can convert the geometry of a planar magnetic device into SPICE simulation netlists. It can accurately capture skin and proximity effects in 1-D multiple winding, multiple layer planar magnetics at high frequencies. It is developed and maintained by Minjie Chen, Stephanie Pavlick, and Samantha Gunter, under the supervision of Prof. David Perreault at MIT in 2014. GNU General Public License v2.0 applies. Contributions and comments are welcome. Please report bugs to minjie@princeton.edu.
Source Code
The solver and GUI of M2Spice was written by Stephanie Pavlick and Minjie Chen in 2014 with Tkinter.
M2Spice Source Code
Download M2Spice
Windows Version
Mac-OS Version
updated on August 13, 2015
Download LTSpice IV
Documentation
Files used in the tutorial.
Example Geometry
Example Netlist
LTspice Time Domain Simulation File
LTspice Frequency Domain Simulation File
Datasheet for EPCOS ELP43 Core
Datasheet for EPCOS N49 Material
updated on Jan 16, 2015
Five suggestions for high frequency planar magnetics modeling
1. Proximity effects can dramatically increase loss.
2. Increasing the copper thickness may increase the winding loss due to proximity effects.
3. Selecting the optimal interleaving strategy is very important.
4. PCB layer stack and layer spacing offer additional design flexibilities.
5. Winding loss and core loss are correlated and should not be isolated. Core loss can impact the current distribution, and current distribution can impact the core loss.
What is M2Spice?
M2Spice is a software tool that can rapidly generate a netlist to analyze and simulate planar magnetics. The theoretical basis of M2Spice is presented as a modular layer model (MLM) in [1].
How to use M2Spice?
The only thing that M2Spice does is generating a netlist that can be used to represent a planar magnetic component in SPICE simulations. The users need to provide the geometry information of the planar magnetic devices to M2Spice (including length, width, copper thickness, etc.). After checking the geometry information, M2Spice will produce a netlist (in .txt format) that can be used for different purposes.
What are the similarities and differences between MLM and other analytical tools?
The MLM follows an analytical framework that models each layer in the planar magnetics device seperately as modular circuit cells, and uses external vias to tie various cells in series or parallel. It is simple and intuitive, and offers a close match between variables in the electrical domain and variables in the magnetic domain. It is closely related to many existing magnetic modeling approaches. Its underlying concept is simlar to the “optical system analogy” approach presented in [2]. by Dr. Keradec. It can be adjusted towards the discretization-oriented model presented in [3]. by Dr. Lopera. The famous Dowell’s formula [4]. and the calculation of mutual resistances [5] are both specific solutions to this modular layer model. The ac resistance in a cylindrical conductor can be rederived from a different perspective compared to the derivation provided in [6]. The model also intuitively illustrates the duality between magnetic circuit and electrical circuit models [7-8].
A brief overview for the Modular Layer Model
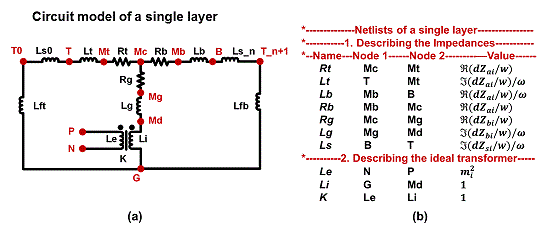
The MLM starts from modeling a single conductor. The electromagnetic field on the surface and inside a single conductor can be described by two KVL equations that can be represented by a “T” shape network as shown in Fig. 1. Two “T” shape networks are linked together by one more KVL equation, formulating a lumped circuit model representing two adjacent layers, as shown in Fig. 2. The two layer model can be easily extended to model planar magnetics with multiple layers. The interactions between the layer stack and the magnetic core can be described by additional KVL equations. Guided by additional KVL equations, the magnetic core is modeled as additional impedances that can be calculated using the reluctance of the magnetic core.
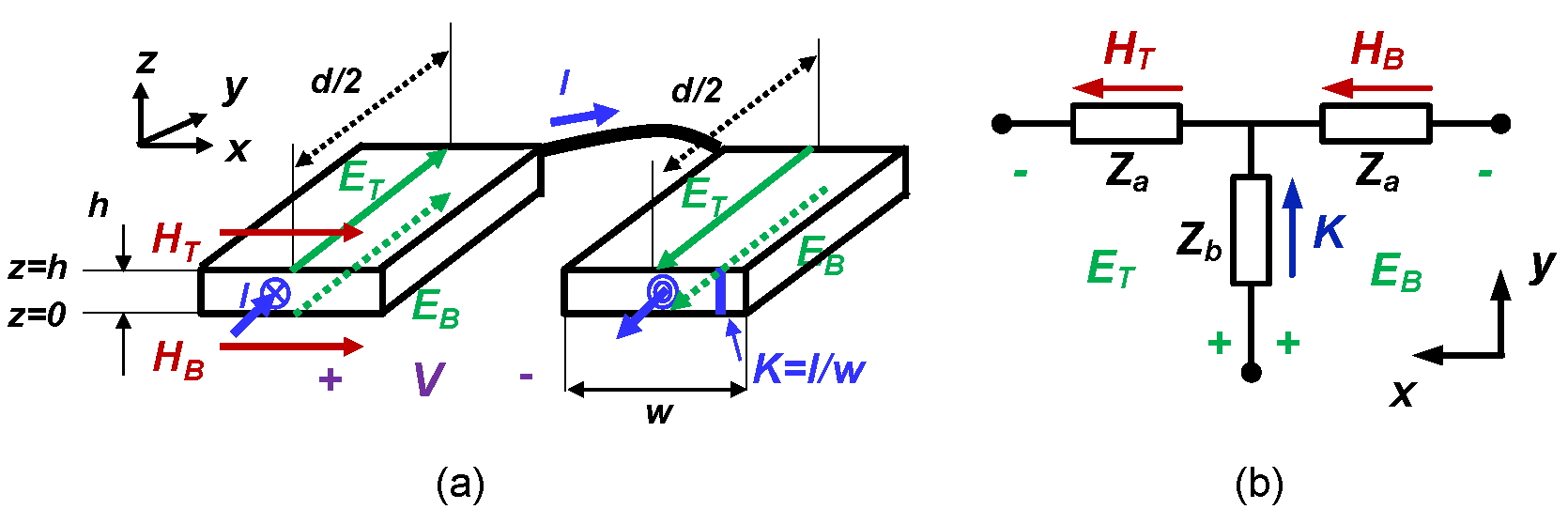 |
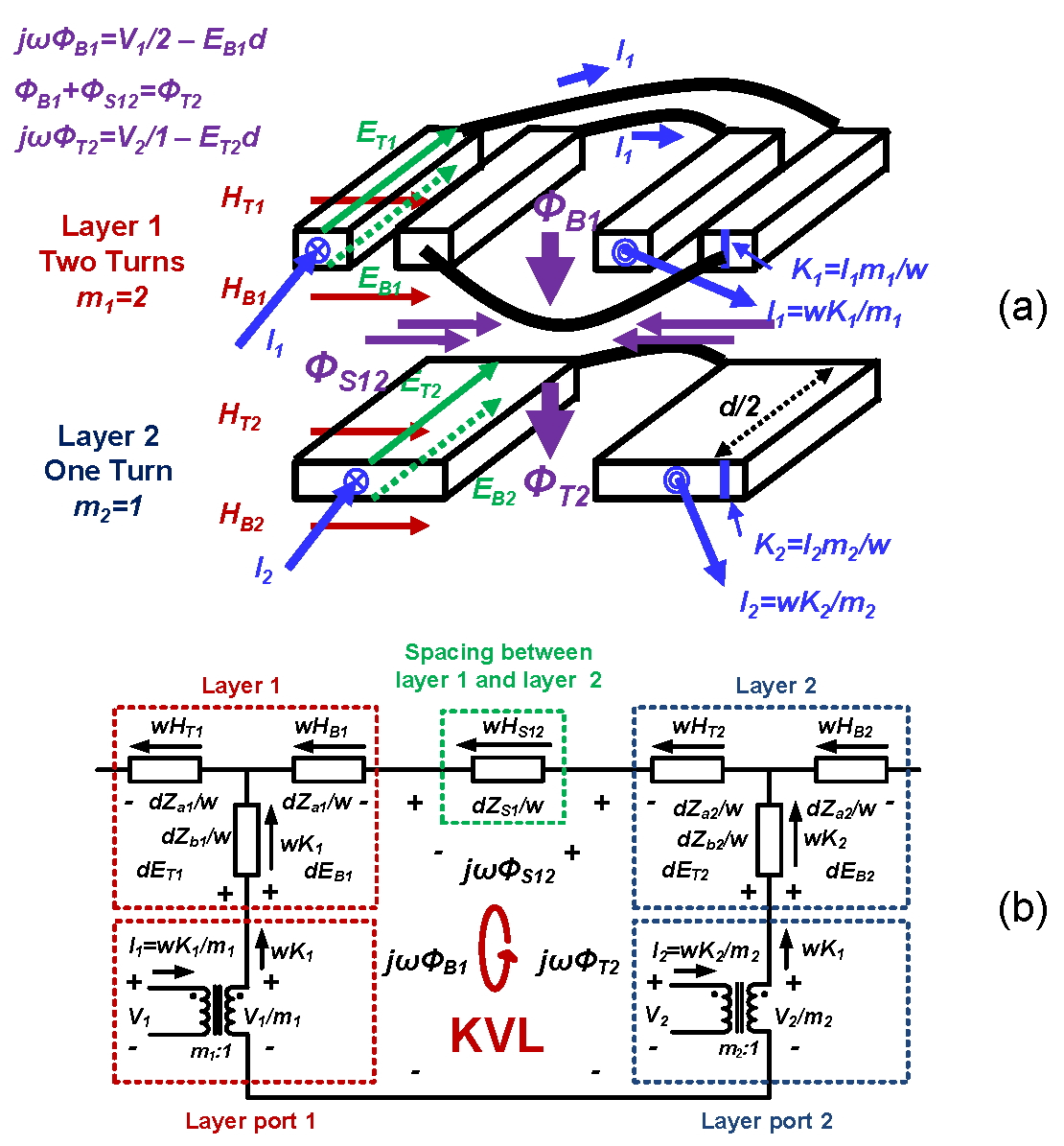 |
Following this approach, a multilayer planar magnetic structure as shown in Fig. 3 can be modeled as a combination of multiple distributed blocks as shown in Fig. 4, and represented by a lumped circuit model consisting of many iterative sub-circuit blocks as shown in Fig 5.
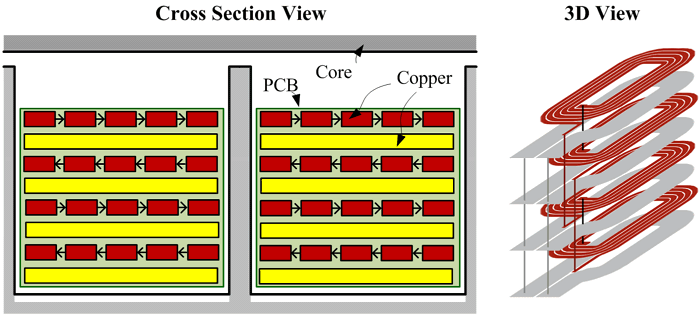 |
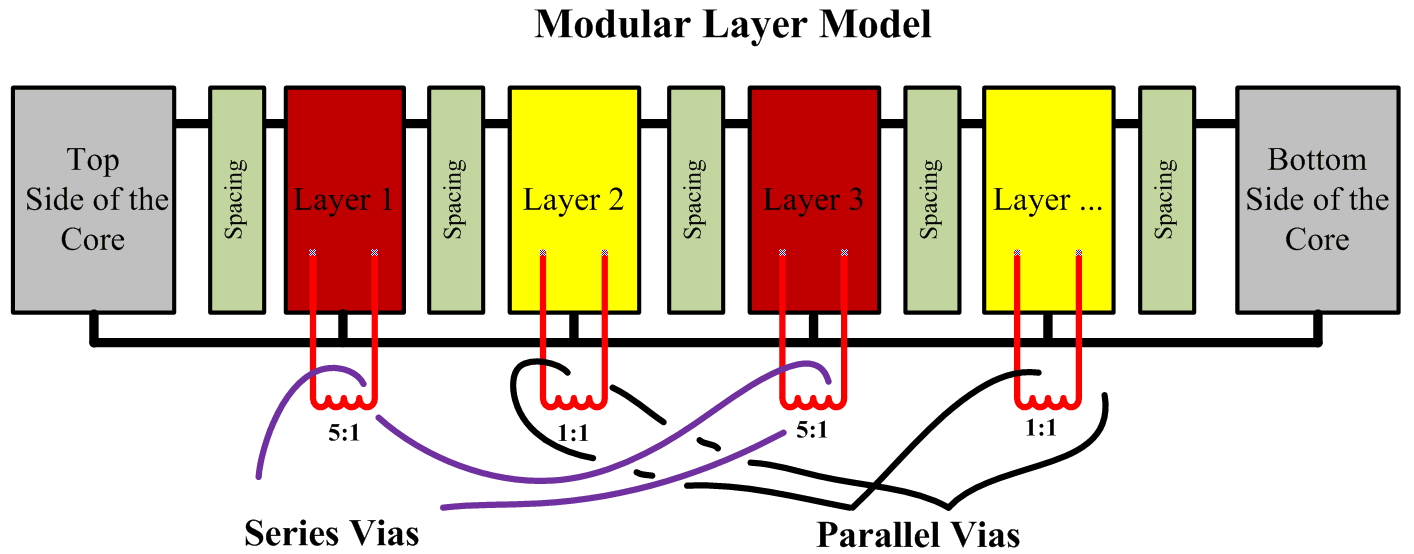 |
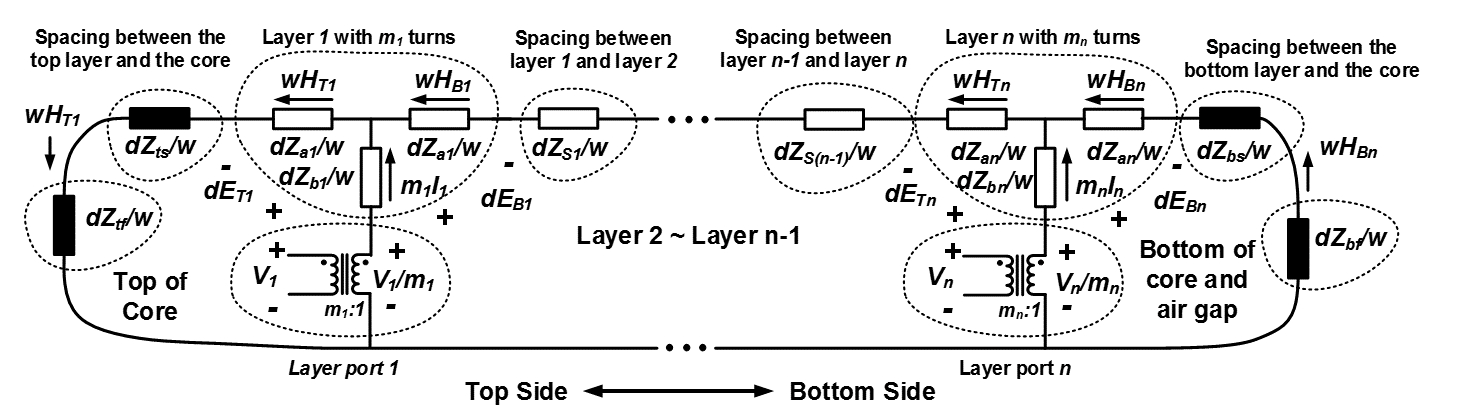 |
The lumped circuit model shown in Fig.5 can be described by a SPICE netlist to be simulated by a SPICE tool. Since the netlist is also highly modularized, the netlists can be rapidly generated by a computer script as implemented in M2Spice.
 |
References
M. Chen, M. Araghchini, K. K. Afridi, J. H. Lang, C. R. Sullivan and D. J. Perreault, “A Systematic Approach to Modeling Impedances and Current Distribution in Planar Magnetics,” IEEE Transactions on Power Electronics vol.31, no.1, pp. 560-580, January, 2016.
J-P. Keradec, B. Cogitore, and F. Blache, “Power transfer in a twowinding transformer: from 1-D propagation to an equivalent circuit,” IEEE Trans. Magn., vol.32, no.1, pp.274-280, Jan. 1996.
J. M. Lopera, M. Pernia, J. Diaz, J. M. Alonso, and F. Nuno, “A complete transformer electric model, including frequency and geometry effects,” Proc. of the IEEE Power Electron. Special. Conf. (PESC), vol.2, pp.1247-1252, June 1992.
P. L. Dowell, “Effects of eddy currents in transformer windings,” Proc. of the Inst. of Elect. Eng., vol.113, no.8, pp.1387-1394, Aug. 1966.
J. H. Spreen, “Electrical terminal representation of conductor loss in transformers,” IEEE Trans. Power Electron., vol.5, no.4, pp.424-429, Oct. 1990.
W. G. Hurley, E. Gath, and J. G. Breslin, “Optimizing the AC resistance of multilayer transformer windings with arbitrary current waveforms,” IEEE Trans. Power Electron., vol.15, no.2, pp.369-376, Mar. 2000.
W. H. Hayt and J. E. Kemmerly, “Inductance and Capacitance: Duality,” in Engineering Circuit Analysis, Fourth Edition, New York: McGraw-Hill Book Company, 1993.
D. C. Hamill, “Lumped equivalent circuits of magnetic components: the gyrator-capacitor approach,” IEEE Trans. Power Electron., vol.8, no.2, pp.97-103, Apr 1993.